CGAL的D维空间搜索(基于KD树)
1、介绍?
????????空间搜索包通过提供支持以下算法的实现来实现精确和近似距离的实现
????????最近和最远邻居搜索
????????精确和近似搜索
????????(近似)范围搜索
????????(近似)k-最近邻和k-最远邻搜索
????????(近似)增量最近邻和增量最远邻搜索
????????表示点和空间对象的查询项。
????????在这些搜索问题中,给定d维空间中的数据点集P。这些点可以用笛卡尔坐标或齐次坐标表示。这些点被预处理成树数据结构,这样给定任何查询项q,P中的点都可以被有效地浏览。近似空间搜索包是针对数据集设计的,这些数据集足够小,可以在主内存中存储搜索结构(与数据库中假设数据驻留在辅助存储中的方法相反)。
????????范围搜索和近似最近邻搜索在搜索目的和算法上有一些区别。范围搜索关注的是落在某个范围内的数据检索,而近似最近邻搜索则专注于在大数据集中找到与查询点最接近的数据点。两者虽然有相似之处,但在应用场景和算法上有各自的特点和要求。
1.1、近似搜索
????????空间搜索支持根据与查询对象之间的距离浏览存储在空间数据结构中的d维空间对象集合。查询对象可以是点或任意空间对象,例如d维球体。空间数据结构中的对象是d维点。
????????通常,要计算的邻居数量事先并不知道,例如,因为数量可能取决于邻居的某些属性(例如,当查询人口超过一百万的巴黎最近的城市时)或到查询点的距离。传统的方法是使用k-最近邻算法的k-最近邻搜索,其中k在调用算法之前是已知的。因此,必须猜测最近邻居的数量。如果猜测太大,则执行冗余计算。如果数量太小,则必须重新调用计算更多邻居的计算,从而执行冗余计算。因此,Hjaltason和Samet引入了增量最近邻搜索,即在获得k个最近邻居后,可以获得第k+1个邻居,而无需从头开始计算第k+1个最近邻居。
????????空间搜索通常由预处理阶段和搜索阶段组成。在预处理阶段,人们构建一个搜索结构,在搜索阶段,人们进行查询。在预处理阶段,用户构建一个存储空间数据的树数据结构。在搜索阶段,用户调用一个搜索方法来浏览空间数据。
????????通过相对较小的修改,最近邻搜索算法可用于查找距离查询对象最远的对象。因此,空间搜索包也支持最远邻搜索。
????????通过放宽对邻居应该精确计算的要求,可以减少精确邻居搜索的执行时间。如果两个对象与查询对象的距离大致相同,而不是精确计算最近/最远的邻居,则其中一个对象可能会被返回为近似最近/最远的邻居。即,给定某个非负常数作为近似 k-最近邻返回的对象的距离不得大于 (1+ε)r
其中,r表示到第k个真实最近邻居的距离。类似的,近似k个最远邻居的距离不得小于r/(1++ε)显然,当 ?=0 时我们得到精确的结果,且也就是说,结果越不精确。
????????在搜索最近邻时,算法会遍历kd树,并且必须为每个节点决定两件事:首先应该访问哪个子节点,以及另一个子节点中是否存在可能的最近邻。这基本上可以归结为计算到较远子节点的距离,因为到较近子节点的距离与到父节点的距离相同。现在有两种选择:
????????一般来说,我们使用给定的度量来计算距离。这是具有一般距离类的k近邻搜索。
????????对于点查询,我们可以“更新”距离,因为它一次只在一个维度上改变。这是正交k近邻搜索,具有正交距离类。以下示例详细展示了正交距离计算
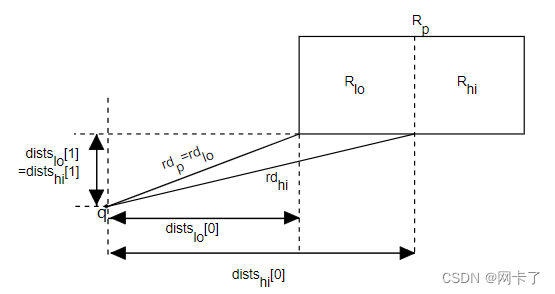
?正交距离计算技术
????????假设我们正在搜索最近邻,从kd-树下降,使用Rp作为父矩形,?Rlo和Rhi作为其孩子在当前步骤。进一步假设Rlo更接近查询点q. 让CD表示切割尺寸,并设 cv表示切割值。此时我们已经知道距离rdp,如果父矩形是矩形,则需要检查Rhi可能包含最近邻。因为 Rlo是较接近的矩形,它到q的距离,rdlo与 rdp 相同。
????????注意,对于每个维度i≠cd, distslo[i]=distshi[i],因为这些坐标不受当前切割的影响。因此,沿着切割尺寸的新距离为 distshi[cd]=cv?q[cd]现在我们可以计算rdhi在恒定时间内(与维度无关),rdhi=rdp?distslo[cd]2+(cv?q[cd])2只有在距离每次只在一个维度上变化的情况下,才能使用这种策略,点查询就是这种情况。
????????以下两个类实现了正交距离的标准搜索策略,如加权闵可夫斯基距离。第二个类是增量邻居搜索和距离浏览的特例。两者都需要扩展节点。
Orthogonal_k_neighbor_search<Traits, OrthogonalDistance, Splitter, SpatialTree>
Orthogonal_incremental_neighbor_search<Traits, OrthogonalDistance, Splitter, SpatialTree>????????另外两个类实现了用于一般距离的标准搜索策略,如用于等距矩形查询的曼哈顿距离。同样,第二个类是增量邻居搜索和距离浏览的特例。?
K_neighbor_search<Traits, GeneralDistance, Splitter, SpatialTree>
Incremental_neighbor_search<Traits, GeneralDistance, Splitter, SpatialTree>1.2、范围搜索
????????使用精确或模糊的d维对象包围一个区域,支持精确范围搜索和近似范围搜索。查询对象的模糊性由参数用于定义对象的内部和外部近似值。例如,在类Fuzzy_sphere中,-半径为r的球体的内部和外部近似值定义为半径为r-ε的球体和r+?分别地使用模糊项目时,查询报告如下:
????????总是报告内部近似值范围内的点。
????????位于外近似值内但不在内近似值内的点可能会或可能不会报告。
????????不在外近似范围内的点永远不会被报告。
????????对于精确范围搜索,模糊参数?设置为零。
????????类Kd_tree在搜索方法中实现了范围搜索,该方法是一个模板方法,具有输出迭代器和概念FuzzyQueryItem的模型,如Fuzzy_iso_box或Fuzzy_sphere。对于大数据集的范围搜索,用户可以将构建kd树时使用的参数bucket_size设置为较大的值(例如100),因为通常查询时间将小于使用默认值的时间。
2、拆分规则 (更详细的了解,请阅读相关论文)
????????用户可以根据数据从以下拆分规则中选择一种,而不是使用下面描述的默认拆分规则 Sliding_midpoint,这些规则决定了如何计算分离超平面。每个拆分器都有退化的最坏情况,这可能会导致线性树和堆栈溢出。将拆分规则切换为另一种将解决该问题。
????????矩形中点:此分割规则通过与最长边垂直的中点切割一个矩形。
????????最大价差中点:此分割规则将矩形切成(Mind+Maxd)/2与具有最大点扩散的维度正交 [Mind,Maxd]。
????????滑动中点:这是矩形分割规则中点的修改。它首先尝试执行如上所述的矩形中点分割。如果数据点位于分离平面的两侧,则滑动中点规则会计算出与矩形中点规则相同的分隔符。如果数据点仅位于一侧,则通过将由矩形中点规则计算出的分隔符滑动到最近的数据点来避免这种情况。
????????当所有中点规则在最长边的中间剪切边界框时,对于一维距离呈指数增加的数据集,树将变为线性。

在2d中设置的中点最坏情况点。
????????矩形中值:拆分维度是矩形最长边的维度。拆分值由沿着该维度的数据点的坐标中值定义。
????????最大分散中位数:拆分维度是矩形最长边的维度。拆分值由沿着该维度的数据点的坐标中值定义。
????????如果许多点在非切割维度的维度上共线,则树可以变为中值规则的线性。
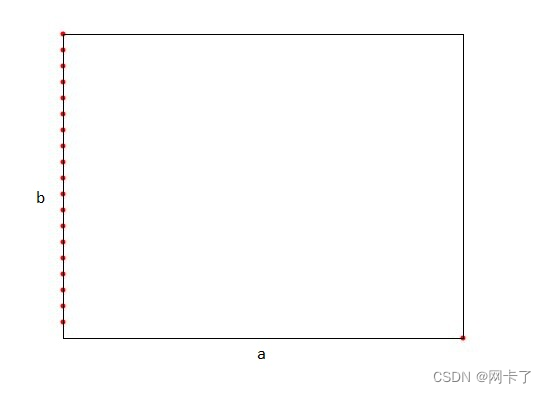
在2d中设置的中值最坏情况点。a比b长,所以这就是切割尺寸。
????????Fair:此分割规则是矩形分割规则的中值和矩形分割规则的中点之间的折衷。此分割规则保持了矩形最长边和最短边最大允许比率的上限(此上限的值在公平分割规则的构造函数中设置)。在满足此限制的分割中,它选择点分布最大的分割。然后,它以尽可能均匀的方式分割点,同时保持对结果矩形比率的限制。
????????Sliding_fair:这个分割规则是公平分割规则和滑动中点规则之间的折衷。滑动公平分割基于这样一种理论,即有两种类型的分割是好的:产生胖矩形的平衡分割,以及提供较少点的矩形为胖的不平衡分割。
????????此外,这种分割规则保持了矩形最长边和最短边最大允许比的上限(该上限的值在公平分割规则的构造函数中设置)。在满足该界限的分割中,它选择点分布最大的分割。然后考虑纵横比界限允许的最极端切割。这是通过将矩形最长边除以纵横比界限来实现的。如果中值切割位于这些极端切割之间,则我们使用中值切割。如果不是,则考虑更接近中值的极端切割。如果所有点都位于该切割的一侧,则我们滑动切割直到它碰到第一个点。这可能会违反纵横比界限,但绝不会产生空单元。
????????KD树是一种数据结构,主要用于存储和组织k维空间中的点。拆分是KD树构建过程中的一个关键步骤,其目的是为了减少树中每个节点的深度,从而提高搜索效率。
????????在KD树中,拆分的主要目的是将一个节点拆分成两个子节点,以减少树的深度。拆分过程通常是在节点中选取一个维度,并在此维度上选择一个值,然后将该节点拆分为两个子节点。左子节点包含所有在该维度上小于该值的点,右子节点包含所有在该维度上大于该值的点。通过这种方式,KD树能够将高维数据空间划分为更小的子空间,使得搜索和查询过程更加高效。
????????总之,拆分是KD树构建过程中的重要步骤,它有助于降低树的深度,从而提高搜索效率。
3、性能
????????我们采用了 aim@shape 的 gargoyle 数据集(Surface),并在 gargoyle 的 bounding box 中生成了相同数量的随机点(Random)。然后,我们考虑了三种场景作为数据/查询。数据集包含 800K 个点。对于每个查询点,我们使用默认拆分器计算 K=10、20、30 个最接近的点,桶大小为 10(默认)和 20。
????????结果是在具有16 GB RAM的Intel i7 2.3 GHz笔记本电脑上使用C++ 6的O3选项编译的C++ 5.1版本生成的。
????????这些值是每次十次测试的平均值。我们以秒为单位显示构建树和查询的时间。
| k | bucket size | Surface Build | Random Build | Surface/Surface | Surface/Random | Random/Random |
|---|---|---|---|---|---|---|
| 10 | 10 | 0.17 | 0.31 | 1.13 | 15.35 | 3.40 |
| 10 | 20 | 0.14 | 0.28 | 1.09 | 12.28 | 3.00 |
| 20 | 10 | (see above) | (see above) | 1.88 | 18.25 | 5.39 |
| 20 | 20 | (see above) | (see above) | 1.81 | 14.99 | 4.51 |
| 30 | 10 | (see above) | (see above) | 2.87 | 22.62 | 7.07 |
| 30 | 20 | (see above) | (see above) | 2.66 | 18.39 | 5.68 |
????????使用树构建算法的并行版本也进行了相同的实验,并并行执行查询:?
| k | bucket size | Surface Build | Random Build | Surface/Surface | Surface/Random | Random/Random |
|---|---|---|---|---|---|---|
| 10 | 10 | 0.07 | 0.12 | 0.24 | 3.52 | 0.66 |
| 10 | 20 | 0.06 | 0.12 | 0.22 | 2.87 | 0.57 |
| 20 | 10 | (see above) | (see above) | 0.41 | 4.28 | 1.02 |
| 20 | 20 | (see above) | (see above) | 0.38 | 3.43 | 0.88 |
| 30 | 10 | (see above) | (see above) | 0.58 | 4.90 | 1.44 |
| 30 | 20 | (see above) | (see above) | 0.60 | 4.28 | 1.28 |
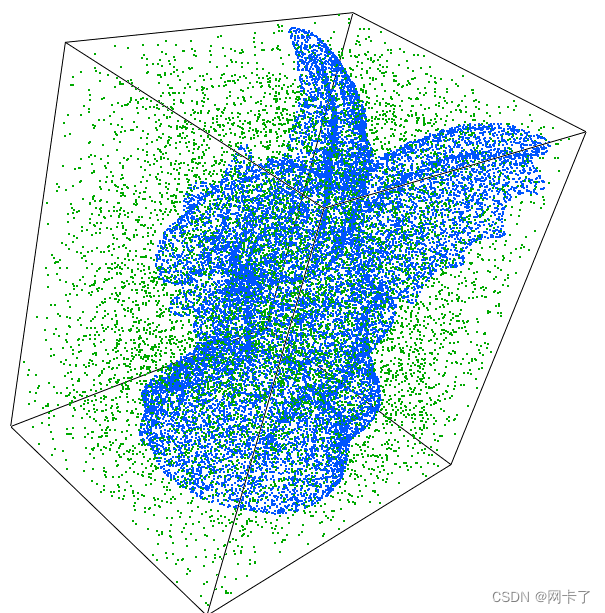
基准数据集(为了可视化而向下采样)。
蓝色:石像表面。绿色:随机bbox?。?
4、软件设计(仅了解)
????????Bentley将kd树引入为高维中二叉查找树的泛化。kd树将空间分层分解为相对较少的矩形,使得没有矩形包含太多的输入对象。对于我们的目的,真实d维空间中的矩形Rd是坐标轴上d个闭区间的乘积。
????????kd树是通过划分Rd中的点集获得的使用(d-1)维超平面。树中的每个节点都被一个这样的分离超平面分成两个子节点。可以使用多种分裂规则(见第节分裂规则)来计算一个分离的(d-1)维超平面。
????????kd树的每个内部节点都与一个矩形和一个与坐标轴之一正交的超平面相关联,该超平面将矩形分成两部分。因此,由分裂维度和分裂值定义的这种超平面称为分隔符。这两个部分与树中的两个子节点相关联。划分空间的过程继续进行,直到矩形中的数据点数量低于某个给定的阈值。与叶节点相关的矩形称为桶,它们将空间细分为矩形。数据点仅存储在树的叶节点中,而不是内部节点中。
????????Friedmann、Bentley和Finkel描述了通过递归搜索kd树来查找第k个最近邻的标准搜索算法。
????????当遇到树的节点时,算法首先访问最接近查询点的子节点。返回时,如果包含另一个子节点的矩形位于1/(1+ ?)乘以到目前为止第k个最近邻居的距离,然后递归访问另一个孩子。优先级搜索[2]在优先级队列的帮助下,按距离队列的递增顺序访问节点。当查询点到最近节点的距离超过到最近点的距离时,搜索停止,其中距离因子为1/(1+ ?)。优先级搜索支持邻近搜索,标准搜索不支持。
????????为了加速高维空间中最近邻搜索中的内部距离计算,近似搜索包支持正交距离计算。正交距离计算实现了Arya和Mount引入的高效增量距离计算技术[1]。该技术仅适用于查询项表示为点且具有二次形式距离的邻居查询,二次形式距离由dA(x,y)=(x-y)A(x-y)T定义其中矩阵A是正定矩阵,即dA(x,y)≥0一类重要的二次型距离是加权闵可夫斯基距离。给定参数p>0参数wi≥0,0<i≤d
加权闵可夫斯基距离定义为 lp(w)(r,q)=(Σi=di=1wi(ri?qi)p)1/p对于0<p<∞并且由l∞(w)(r,q)=max{wi|ri?qi|∣1≤i≤d}定义曼哈顿距离(p=1,wi=1)和欧几里得距离(p=2,wi=1
)是加权闵可夫斯基度量的例子。
????????为了加快距离计算,还使用了转换后的距离而不是距离本身。例如,对于欧几里得距离,为了避免昂贵的平方根计算,使用平方距离而不是欧几里得距离本身。
????????不在树内存储点坐标通常会产生大量的缓存缺失,从而导致性能不佳。例如,当索引存储在树内时,或者在较小程度上当点坐标存储在动态分配的数组中时(例如,具有动态维度的Epick_d)——我们说“在较小程度上”,因为点在构造后由kd-tree以缓存友好的顺序重新创建,因此坐标更有可能以近乎最优的顺序存储在堆上。在这种情况下,可以将Kd_tree类的EnablePointsCache模板参数设置为Tag_true。然后,点坐标将以最佳方式缓存。这将增加内存消耗,但提供更好的搜索性能。使用这种缓存时,请参见GeneralDistance和FuzzyQueryItem概念以了解其他要求。
5、其他
????????CGAL::Weighted_Minkowski_distance?是 CGAL 库中的一个类,用于计算加权 Minkowski 距离。Minkowski 距离是欧几里得距离和曼哈顿距离的一种泛化,通过引入一个参数 p 来控制距离的计算方式。而加权 Minkowski 距离则进一步引入了权重因子,用于对不同维度上的距离进行加权。
????????加权 Minkowski 距离的计算公式如下:
????????D(p, w) = (∑_i=1^n |x_i - y_i|^p * w_i)^(1/p)
????????其中,p 是一个正整数参数,w 是一个权重向量,x 和 y 是两个点。
????????在?CGAL::Weighted_Minkowski_distance?类中,你可以设置参数 p 和权重向量 w,然后使用该类来计算点之间的加权 Minkowski 距离。这个距离度量在计算机图形学、模式识别和机器学习等领域中非常有用,因为它可以根据不同维度的重要性进行灵活的加权。
????????使用?CGAL::Weighted_Minkowski_distance?类,你可以方便地集成加权 Minkowski 距离计算到你的几何算法和数据结构中,以实现更精确和灵活的几何分析和处理。
????????Neighbor_search::Point_with_transformed_distance结构在CGAL中用于存储最近邻点的信息和经过变换后的距离,以便更好地处理和分析几何数据。
????????在CGAL库中,KD树(k-dimension tree)是一种常用的数据结构,用于存储和查询多维空间中的点。而Splitter则是用于分割KD树的组件,它的作用是在预处理阶段将KD树分割成更小的子树,以便更有效地进行后续处理。
????????不同的Splitter方法可能会导致不同的结果,因为它们采用不同的策略来分割KD树。不同的Splitter方法可能会在分割方式和平衡性方面有所不同,这会对KD树的查询效率和使用效果产生影响。
Vertex_point_pmap vppmap = get(CGAL::vertex_point,mesh);
Tree tree(vertices(mesh).begin(), vertices(mesh).end(), Splitter(), Traits(vppmap));????????CGAL::Euclidean_distance是一个函数对象,用于计算两个点之间的欧几里得距离。在CGAL库中,它被用作一个度量标准,用于确定两个点之间的相似性或差异性。?
????????线段树和KD树都是处理数据结构和算法中的空间分割问题的数据结构,但它们之间存在明显的区别。
????????线段树是一种二叉搜索树,它将一个区间划分成一些单元区间,每个单元区间对应线段树中的一个叶结点。线段树可以快速地查找某一个节点在若干条线段中出现的次数,时间复杂度为O(logN)。而未优化的空间复杂度为2N,实际应用时一般还要开4N的数组以免越界,因此有时需要离散化让空间压缩。
????????而KD树是一种将k维数据空间进行二分搜索的树状数据结构。它的每一个节点表示k维空间中的一个点,每个内部节点表示一个超平面,该超平面对其子空间进行分割。对于k维空间中的n个点,构建一棵KD树需要进行n-1次分裂操作,每次选择一个维度,然后在该维度上选择一个分裂点。这样就可以得到两个子空间,其中一个只包含原空间中的半数点,另一个包含剩余的点。然后对这两个子空间递归地执行上述分裂操作,直到每个子空间只包含一个点为止。
????????总的来说,线段树和KD树在处理问题的维度和数据结构上有所不同。线段树主要处理一维问题,而KD树主要处理多维问题。在实际应用中,根据问题的性质和需求选择合适的数据结构是非常重要的。
????????CGAL::Orthogonal_k_neighbor_search是CGAL库中的一个函数,用于在k维空间中执行最近邻搜索。它采用一种高效的方法来搜索最近邻,特别是在高维空间中。该函数采用k-最近邻搜索算法,可以快速找到查询点在k维空间中最接近的k个邻居。
????????在使用CGAL::Orthogonal_k_neighbor_search时,需要指定查询点的集合和搜索的半径。该函数将返回与查询点距离在指定半径内的所有点,并按距离进行排序。默认情况下,该函数使用欧几里得距离作为距离度量,但也可以使用其他距离度量。
????????CGAL::Orthogonal_incremental_neighbor_search是CGAL库中的一个函数,用于执行增量式的最近邻搜索。它是一种高效的算法,特别适用于需要在连续查询中不断更新最近邻列表的情况。
????????该函数采用增量搜索的方式,逐步增加搜索范围,以找到更接近的邻居。在每次迭代中,它都会更新最近邻列表,并使用近似搜索来快速定位潜在的最近邻。通过这种方式,它可以在保持相对较低的时间复杂度的同时,提供较好的搜索结果。
????????CGAL::Search_traits_2是CGAL库中的一个模板类,用于定义二维空间中点的搜索特性。它提供了用于执行几何搜索所需的基本数据结构和操作,例如点的存储和比较。
????????CGAL::Search_traits_2类模板接受两个参数:Point和Less_xy_2。Point是一个表示二维点的类,而Less_xy_2是一个谓词,用于比较两个点的x和y坐标。该模板类提供了用于执行几何搜索所需的基本操作,例如点的存储、比较和排序。
???????????????CGAL的Iso_box_d是一个模板类,用于表示多维空间中的等距盒子。等距盒子是一种几何对象,其边界由平行于坐标轴的超平面构成。Iso_box_d类提供了创建、复制和操作等距盒子的功能。
???????????????CGAL::Filter_iterator是CGAL库中的一个迭代器适配器,用于过滤容器中的元素。它接受一个输入迭代器和一个谓词(Predicate),并将该谓词应用于容器中的每个元素。只有满足谓词条件的元素才会被包括在过滤后的迭代器范围内。
???????????????CGAL::Manhattan_distance_iso_box_point是一个用于计算等距盒子与点之间的曼哈顿距离的函数对象。曼哈顿距离是一种计算两点之间距离的方法,它按照网格线移动,而不是直线移动。在二维空间中,曼哈顿距离等于两点之间水平距离和垂直距离的绝对值之和。
????????CGAL::K_neighbor_search是CGAL库中的一个函数,用于在k维空间中执行最近邻搜索。该函数接受一个查询点的集合、k值和搜索半径作为参数,并返回与查询点距离在指定半径内的所有点,并按距离进行排序。
????????CGAL::K_neighbor_search使用一种高效的数据结构来存储和组织空间中的点,以便快速执行最近邻搜索。它可以用于处理高维空间中的搜索问题,特别是在处理大规模数据集时。
????????CGAL::Fuzzy_sphere和CGAL::Fuzzy_iso_box是CGAL库中的两个类,它们都实现了模糊几何对象的概念。
????????CGAL::Fuzzy_sphere表示模糊球体。模糊球体是一种扩展了球体概念的几何对象,允许球体边界有一定的模糊性。Fuzzy_sphere类提供了一种表示和操作模糊球体的方式,可以用于处理具有模糊边界的几何问题。
????????CGAL::Fuzzy_iso_box表示模糊等距盒子。模糊等距盒子是一种扩展了等距盒子概念的几何对象,允许盒子的边界有一定的模糊性。Fuzzy_iso_box类提供了一种表示和操作模糊等距盒子的方式,可以用于处理具有模糊边界的几何问题。
????????这两个类都提供了一些基本的操作,例如计算模糊对象之间的交、并、差等运算,以及判断一个点是否在模糊对象内等。它们还支持自定义操作,允许用户根据具体需求定义自己的运算和操作。
????????总的来说,CGAL::Fuzzy_sphere和CGAL::Fuzzy_iso_box都是为了解决具有模糊边界的几何问题而设计的类,提供了一种灵活的方式来表示和处理模糊几何对象。
????????CGAL的Splitter是一个用于数据分割的组件,特别适用于处理大规模数据集。它的作用是在数据预处理阶段,将大规模数据集分割成较小的子集,以便更有效地进行后续处理。
????????Splitter通常与数据结构如KD-tree或四叉树一起使用。这些数据结构用于组织和存储空间中的点,以便能够快速进行最近邻搜索。然而,当数据集非常大时,KD-tree或四叉树可能会变得非常大,占用大量内存,甚至可能导致内存溢出。
????????为了解决这个问题,我们需要一种方法来分割KD-tree或四叉树,以便在内存中更有效地存储和处理数据。这时,CGAL的Splitter就发挥了重要作用。
????????CGAL的Splitter使用一种称为“分割线方法”的技术来分割KD-tree或四叉树。该方法通过找到一个直线(或超平面),该直线可以将空间分成两个不相交的子集,然后将该直线作为分割线来分割KD-tree或四叉树。通过这种方式,可以将大型KD-tree或四叉树分割成更小的子树,从而更有效地在内存中存储和处理数据。
????????使用CGAL的Splitter可以显著提高处理大规模数据集的效率,并减少内存使用。这使得我们能够处理更大的数据集,同时保持高效的性能。在需要进行大规模数据处理和搜索的应用中,例如数据库搜索、图像处理和机器学习等领域,CGAL的Splitter具有重要的应用价值。
????????boost::counting_iterator?是 Boost C++ 库中的一个迭代器适配器,它生成一个可以遍历从 0 到给定值的计数序列的迭代器。这个迭代器可以与 STL(Standard Template Library)算法和容器一起使用,以实现更灵活和通用的迭代。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!