图像处理—小波变换

小波变换

一维小波变换

因为存在$L^2(\mathbf{R})=V_{j_0}\oplus W_{j_0}\oplus W_{j_0+1}\oplus ?$，所以存在$f(x)$可以在子空间$V_{j_0}$中用尺度函数展开和在子空间$W_{j_0}{W}_{j_{0+1}},?$中用某些数量的小波函数展开来表示。即

$$f(x)=\sum _k{c}_{j_0}(k){\phi }_{j_0,k}(x)+\sum _{j=j_0}^{\infty }\sum _k{d}_j(k){\psi }_{j,k}(x)$$
其中 $j_0$ 是任意的开始尺度，$c_{j_0}(k)$通常称为近似和或尺度系数，$d_j(k)$称为细节和或小波系数。

由于双正交的性质可得
$$\begin{gathered} c_{j_0}(k)=?f(x),{\phi }_{j_0,k}(x)?=\int f(x){\phi }_{j_0,k}(x)\mathrm{d}x \\ {d}_j(k)=?f(x),{\psi }_{j,k}(x)?=\int f(x){\psi }_{j,k}(x)\mathrm{d}x \end{gathered}$$
转换成离散形式可得
$$\begin{array}{rl}{W}_{\phi }(j_0,k)& =\frac{1}{\sqrt{M}}\sum _{n}f(n){\phi }_{j_0,k}(n)\\ W_{\psi }(j,k)& =\frac{1}{\sqrt{M}}\sum _{n}f(n){\psi }_{j,k}(n),j\ge j_0\end{array}$$
其中 ${\phi }_{j_0,k}(n)$ 和${\psi }_{j,k}(n)$是基函数${\phi }_{j_0,k}(x)$ 和${\psi }_{j,k}(x)$ 的取样形式。

由此可得
$$f(n)=\frac{1}{\sqrt{M}}\sum _k{W}_{\phi }(j_0,k){\phi }_{j_0,k}(n)+\frac{1}{\sqrt{M}}\sum _{j=j_0}^{\infty }\sum _k{W}_{\psi }(j,k){\psi }_{j,k}(n)$$
通常$j_0=0$，$M$为2 的幂(即$M=2^j)$

而对于哈尔小波，离散的尺度和小波函数与$M\times M$哈尔矩阵的行相对应，其中最小尺度为0，最大尺度为$j?1$

快速小波变换

对于图像的多分辨率变换
$$\phi (x)=\sum _n{h}_{\phi }(n)\sqrt{2}\phi (2x?n)$$
并进行尺度化与平移操作，可得
$$\begin{array}{rl}\phi (2^{j}x?k)& =\sum _n{h}_{\phi }(n)\sqrt{2}\phi \left(2(2^{j}x?k)?n\right)\\ & =\sum _m{h}_{\phi }(n)\sqrt{2}\phi (2^{j+1}x?2k?n)\end{array}$$
令$m=2k+n$，可得
$$\begin{array}{r}\begin{array}{rl}\phi (2^{j}x?k)& =\sum _n{h}_{\phi }(n)\sqrt{2}\phi \left(2(2^{j}x?k)?n\right)\\ & =\sum _m{h}_{\phi }(n)\sqrt{2}\phi (2^{j+1}x?2k?n)\\ & =\sum _m{h}_{\phi }(m?2k)\sqrt{2}\phi (2^{j+1}x?m)\end{array}\end{array}$$
同理对于小波函数存在
$$\psi (2^{j}x?k)=\sum _m{h}_{\psi }(m?2k)\sqrt{2}\phi (2^{j+1}x?m)$$
其中将${\psi }_{j,k}(x)=2^{j/2}\psi (2^{j}x?k)$代入$d_j(k)=?f(x),{\psi }_{j,k}(x)?=\int f(x){\psi }_{j,k}(x)\mathrm{d}x$可得
$$d_j(k)=\int f(x)2^{j/2}\psi (2^{j}x?k)\mathrm{d}x$$
又因为$\psi (2^{j}x?k)={\sum }_m{h}_{\psi }(m?2k)\sqrt{2}\phi (2^{j+1}x?m)$

所以存在
$$\begin{array}{rl}{d}_j(k)& =\int f(x)2^{j/2}[\sum _m{h}_{\psi }(m?2k)\sqrt{2}\phi (2^{j+1}x?m)]\mathrm{d}x\\ & =\sum _m{h}_{\psi }(m?2k)[\int f(x)2^{(j+1)/2}\phi (2^{j+1}x?m)\mathrm{d}x]\\ & =\sum _m{h}_{\psi }(m?2k)c_{j+1}(m)\end{array}$$
同理可得
$$c_j(k)=\sum _m{h}_{\phi }(m?2k)c_{j+1}(m)$$
即
$$\begin{array}{rl}{W}_{\psi }(j,k)& =\sum _m{h}_{\psi }(m?2k)W_{\phi }(j+1,m)\\ W_{\phi }(j,k)& =\sum _m{h}_{\phi }(m?2k)W_{\phi }(j+1,m)\end{array}$$
上式揭示了相邻尺度直接的离散小波变换(DWT)系数之间的关系，可以认为是$W_{\phi }(j+1,m),W_{\psi }(j+1,m)$分别与$h_{\phi }(?n),h_{\psi }(?n)$进行卷积操作并下采样得到的，于是可以写成
$$\begin{gathered} W_{\psi }(j,k)=h_{\psi }(?n)?W_{?}(j+1,n){|}_{n=2k,k?0} \\ {W}_{\phi }(j,k)=h_{\phi }(?n)?W_{\phi }(j+1,n){|}_{n=2k,k?0} \end{gathered}$$
即如下图所示的结构

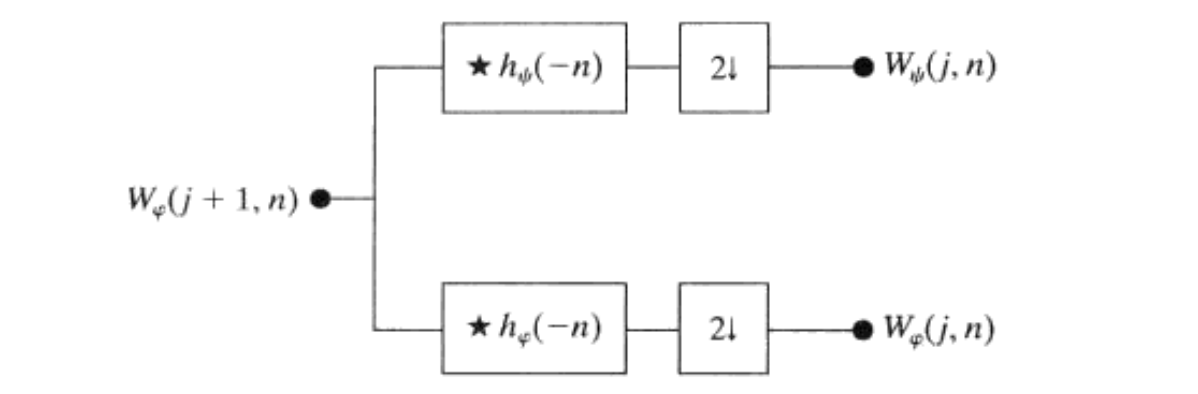
同时可以经过多次迭代分解，如下图是二级分解的结构

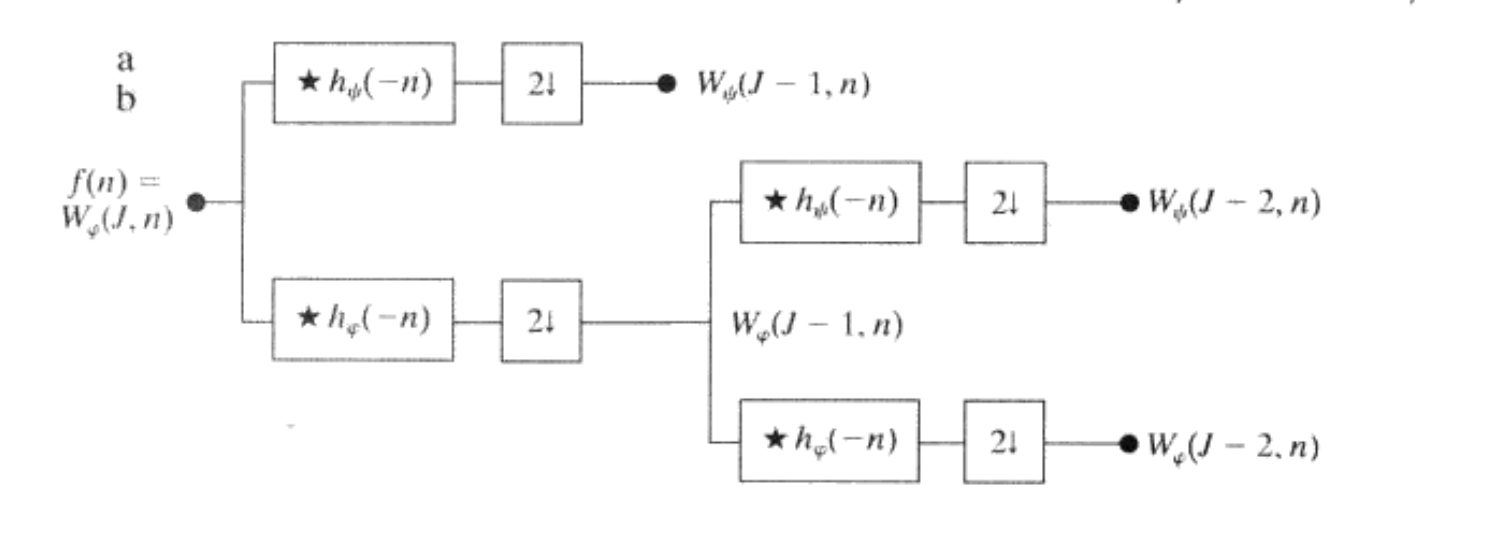
二维小波变换

为了将小波变换扩展到适应二维的图像，由此定义，存在尺度函数
$$\phi (x,y)=\phi (x)\phi (y)$$
以及三个对方向敏感的小波函数
$$\begin{array}{rl}& {\psi }^H(x,y)=\psi (x)\phi (y)\\ & {\psi }^V(x,y)=\phi (x)\psi (y)\\ & {\psi }^D(x,y)=\psi (x)\psi (y)\end{array}$$
以上三个小波函数分别对应图像沿着列方向的变换、图像沿着行方向的变换、图像沿着对角线方向的变换

并存在
$$\begin{array}{c}{\phi }_{j,m,n}(x,y)=2^{j/2}\phi (2^{j}x?m,2^{j}y?n)\\ {\psi }_{j,m,n}^i(x,y)=2^{j/2}{\psi }^i(2^{j}x?m,2^{j}y?n),i=\{H,V,D\}\end{array}$$
并可以推导出离散形式的小波变换
W φ ( j 0 , m , n ) = 1 M N ∑ x = 0 M ? 1 ∑ y = 0 N ? 1 f ( x , y ) φ j 0 , m , n ( x , y ) W ψ i ( j , m , n ) = 1 M N ∑ x = 0 M ? 1 ∑ y = 0 N ? 1 f ( x , y ) ψ j , m , n i ( x , y ) , i = { H , V , D } \begin{aligned} W_{\varphi}(j_{0},m,n)&=\frac{1}{\sqrt{MN}}\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)\varphi_{j_{0},m,n}(x,y)\\\\ W_{\psi}^{i}(j,m,n)&=\frac{1}{\sqrt{MN}}\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)\psi_{j,m,n}^{i}(x,y),i=\{H,V,D\}\end{aligned} Wφ?(j0?,m,n)Wψi?(j,m,n)?=MN ?1?x=0∑M?1?y=0∑N?1?f(x,y)φj0?,m,n?(x,y)=MN ?1?x=0∑M?1?y=0∑N?1?f(x,y)ψj,m,ni?(x,y),i={H,V,D}?
其中$j_0$表示任意的开始尺度，$W_{\phi }(j_0,m,n)$表示在尺度为$j_0$时的近似， W ψ i ( j , m , n ) , i = { H , V , D } W_{\psi}^{i}(j,m,n),i=\{H,V,D\} Wψi?(j,m,n),i={H,V,D}表示对尺度为$j_0$时的水平、垂直与对角线方向的细节

当$j_0=0,M=N=2^j$时，存在离散小波逆变换
$$\begin{array}{rl}f(x,y)& =\frac{1}{\sqrt{MN}}\sum _m\sum _n{W}_{\phi }(j_0,m,n){\phi }_{j_0,m,n}(x,y)\\ & +\frac{1}{\sqrt{MN}}\sum _{i=H.V.D}\sum _{j=j_0}^{\infty }\sum _m\sum _n{W}_{\psi }^i(j,m,n){\psi }_{j,m,n}^i(x,y)\end{array}$$
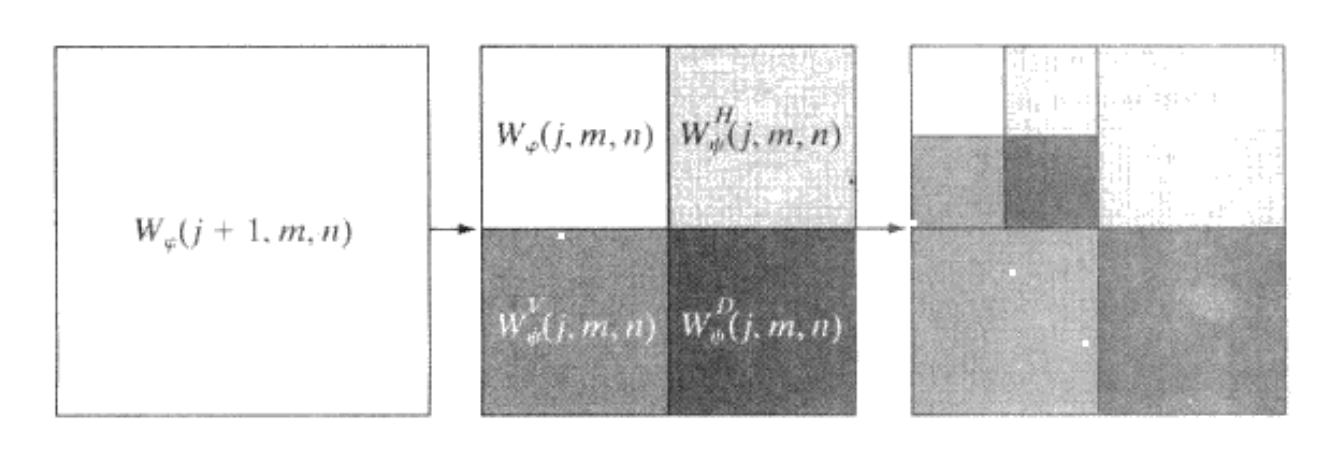
同理可以得到

小波分解过程如图所示

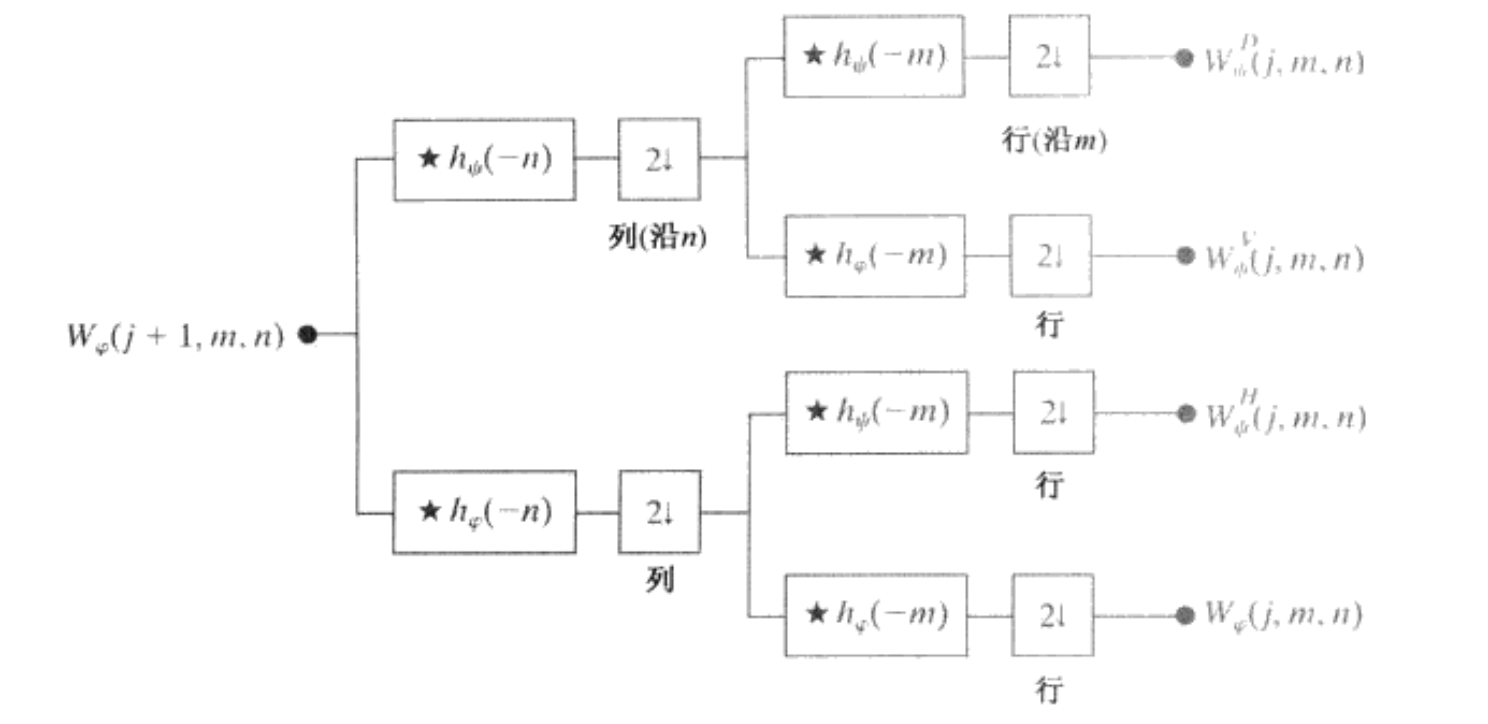
小波逆变换过程如图所示

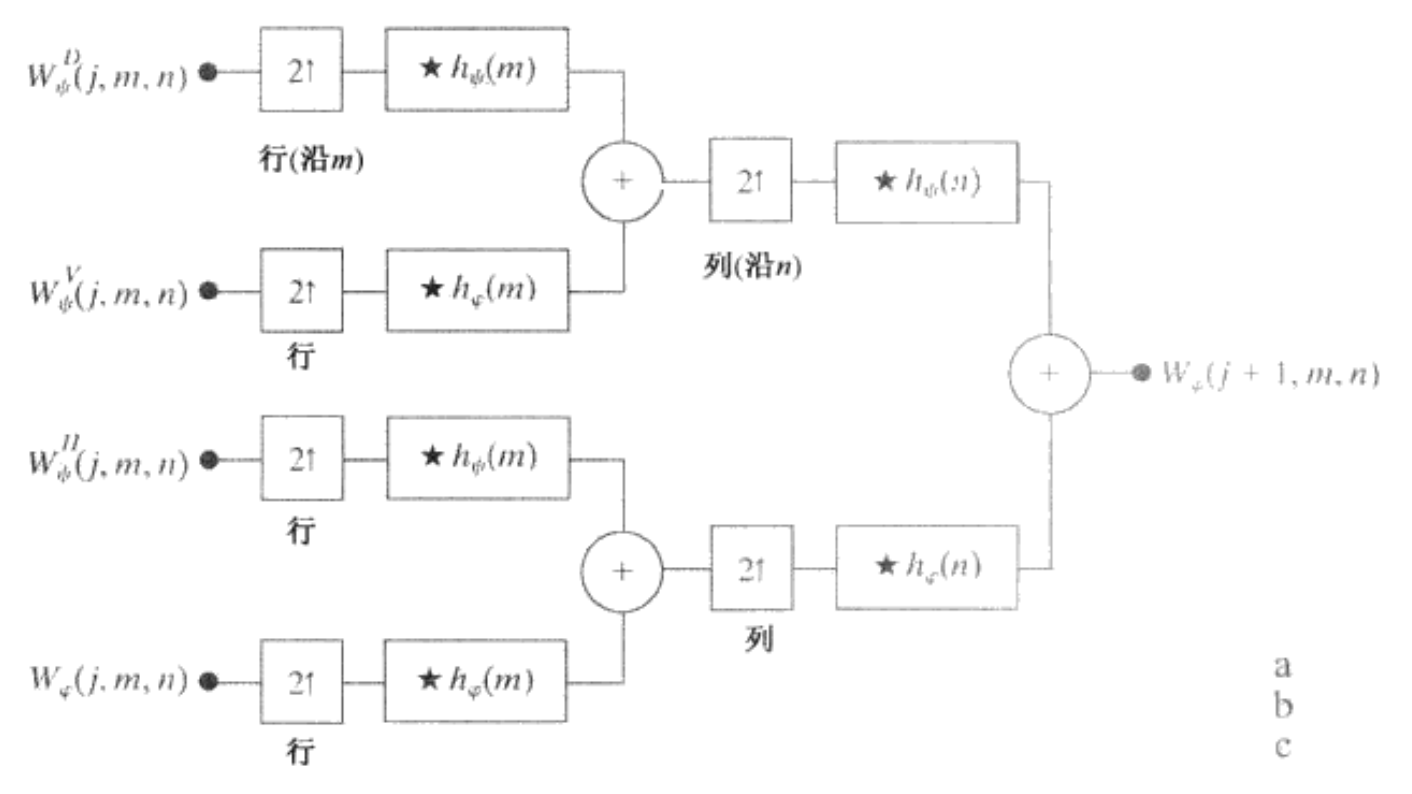
其小波分解的结果如图所示