面试算法96:字符串交织
题目
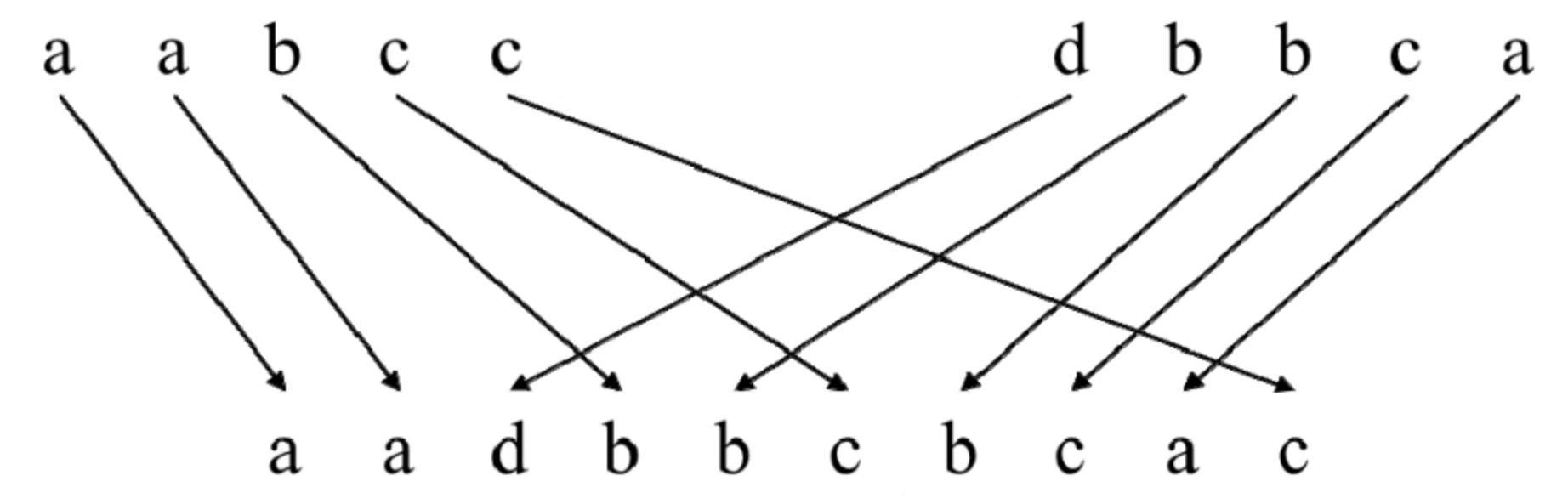
输入3个字符串s1、s2和s3,请判断字符串s3能不能由字符串s1和s2交织而成,即字符串s3的所有字符都是字符串s1或s2中的字符,字符串s1和s2中的字符都将出现在字符串s3中且相对位置不变。例如,字符串"aadbbcbcac"可以由字符串"aabcc"和"dbbca"交织而成。
分析
每步从字符串s1或s2中选出一个字符交织生成字符串s3中的一个字符,那么交织生成字符串s3中的所有字符需要多个步骤。每步既可能从字符串s1中选择一个字符,也可能从字符串s2中选择一个字符,也就是说,每步可能面临两个选择。完成一件事情需要多个步骤,而且每步都可能面临多个选择,这个问题看起来可以用回溯法解决。
这个问题并没有要求列出所有将字符串s1和s2交织得到字符串s3的方法,而只是判断能否将字符串s1和s2交织得到字符串s3。如果能够将字符串s1和s2交织得到字符串s3,那么将字符串s1和s2交织得到字符串s3的方法的数目大于0。这只是判断问题的解是否存在(即判断解的数目是否大于0),因此这个问题更适合应用动态规划来解决。
可以用函数f(i,j)表示字符串s1的下标从0到i的子字符串(记为s1[0…i],长度为i+1)和字符串s2的下标从0到j的子字符串(记为s2[0…j],长度为j+1)能否交织得到字符串s3的下标从0到i+j+1(记为s3[0…i+j+1],长度为i+j+2)的子字符串。f(m-1,n-1)就是整个问题的解。
当s3[i+j+1]和s1[i]相同时,f(i,j)的值等于f(i-1,j)的值。类似地,当s3[i+j+1]和s2[j]相同时,f(i,j)的值等于f(i,j-1)的值。如果s1[i]和s2[j]都和s3[i+j+1]相同,此时只要f(i-1,j)和f(i,j-1)有一个值为true,那么f(i,j)的值为true。
解
public class Test {
public static void main(String[] args) {
boolean result = isInterleave("aabcc", "dbbca", "aadbbcbcac");
System.out.println(result);
}
public static boolean isInterleave(String s1, String s2, String s3) {
if (s1.length() + s2.length() != s3.length()) {
return false;
}
boolean[][] dp = new boolean[s1.length() + 1][s2.length() + 1];
dp[0][0] = true;
// 列为0,没有取用s2字符串的数字
for (int i = 0; i < s1.length(); i++) {
dp[i + 1][0] = s1.charAt(i) == s3.charAt(i) && dp[i][0];
}
// 行为0,没有取用s1字符串的数字
for (int j = 0; j < s2.length(); j++) {
dp[0][j + 1] = s2.charAt(j) == s3.charAt(j) && dp[0][j];
}
for (int i = 0; i < s1.length(); i++) {
for (int j = 0; j < s2.length(); j++) {
char ch1 = s1.charAt(i);
char ch2 = s2.charAt(j);
char ch3 = s3.charAt(i + j + 1);
// 注意是dp[i + 1][j + 1]
dp[i + 1][j + 1] = (ch1 == ch3 && dp[i][j + 1]) || (ch2 == ch3 && dp[i + 1][j]);
}
}
return dp[s1.length()][s2.length()];
}
}
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!