图像各类评价指标合集--(针对LLIE任务)
文章目录
前言
在涉及图像领域,不论时图像复原、图像去噪或者是图像增强等任务,除了人为主观因素上对其进行评价,还需要一些客观的评价指标辅助判断任务完成的好坏。因此本文主要介绍一些图像各类评价的指标,并给出具体的实现代码。
一、常见评价指标
1、均方误差(MSE)
- 定义:对于标准图像 I I I 和待评价图像 K K K , M S E MSE MSE 指的是 I I I 和 K K K 的所有像素值的差的平方和,再求平均值。
- MSE越大,图像质量越好。
- 数学公式:

- 实现代码:
import numpy as np
def MSE(img1,img2):
img1 = img1.astype(np.float64)
img2 = img2.astype(np.float64)
mse = np.mean((img1 - img2) ** 2 )
return mse
2、峰值信噪比(PSNR)
-
定义:通过比较原始信号(通常是未经压缩的图像)和失真信号(压缩或传输后的图像)之间的信噪比来评估图像的失真程度
-
PSNR越大,图像质量越好。
-
数学公式:

其中, M A X I MAX_{I} MAXI? 表示图像颜色的最大数值,8位采样点表示为255。 -
实现代码:
def PSNR(img1, img2):
img1 = img1.astype(np.float64)
img2 = img2.astype(np.float64)
mse = np.mean((img1 - img2) ** 2 )
if mse < 1.0e-10:
return 100
return 10 * math.log10(255.0**2/mse)
- 也可用python自带函数实现
from skimage.metrics import peak_signal_noise_ratio as psnr
3、结构相似性(SSIM)
- 定义:SSIM综合亮度、对比度和结构3个方面来评估图像的质量。
- SSIM越大,图像质量越好。
- 数学公式:计算
x
、
y
x、y
x、y两幅图像的SSIM为:

l 、 c 、 s l、c、s l、c、s 分别为亮度、对比度和结构评价。计算公式如下:

μ \mu μ表示图像的均值, σ x \sigma_{x} σx?表示图像的标准差, σ x y \sigma_{xy} σxy?表示两幅图像的协方差, c 1 、 c 2 、 c 3 c1、c2、c3 c1、c2、c3均为常数 α 、 β 、 γ \alpha 、β、γ α、β、γ为大于0的常数系数。 - 实现代码:
实现步骤不难,方便一点采用自带函数实现from skimage.metrics import structural_similarity。
| ---------->>>><<<<<<---------- |
- 以上常见的评价指标应用范围很广,经常使用,属于评价方法中的全参考方法。
- 实际上,整个图像的质量评价方法可以分为以下3类:
1、全参考(
F
R
?
I
Q
A
FR-IQA
FR?IQA):使用参考图像与待评估图像之间的比较来进行评估。
2、半参考(
R
R
?
I
Q
A
RR-IQA
RR?IQA):使用部分参考信息进行评估。它们既考虑了待评估图像的质量特征,又考虑了部分参考图像的信息。
3、无参考(
N
R
?
I
Q
A
NR-IQA
NR?IQA):不依赖于任何参考图像,仅根据待评估图像自身的内容来进行评估。这些方法主要基于图像的统计性质、纹理特征、对比度等进行评估。
2、低照度图像评价
以下重点介绍一些用于低照度图像的评价指标,方便在LLIE方向上学习的伙伴们。
2.1 均值
- 反映图像的明暗程度,其值越大,亮度越高。
- 代码:
import cv2
def avg(img):
mean_value = np.mean(cv2.normalize(img, None, 0, 255, cv2.NORM_MINMAX))
return round(mean_value,2)
2.2 标准差(Standard Deviation,SD)
- 反映图像对比度,其值越大,对比度越高。
- 代码:
import cv2
def std(img):
img = cv2.normalize(img, None, 0, 255, cv2.NORM_MINMAX)
std = np.std(img)
return round(std,2)
2.3 信息熵(Information Entropy,IE)
- 描述图像信息量,其值越大,信息越丰富。
- 数学公式:

其中, p i 表示图像中某一灰度值所占比例 其中,p_{i}表示图像中某一灰度值所占比例 其中,pi?表示图像中某一灰度值所占比例
- 代码:
import numpy as np
import cv2
def entropy(image):
# 将图像转换为灰度图像
image= cv2.normalize(image, None, 0, 255, cv2.NORM_MINMAX)
gray_image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
# 计算像素值的直方图
histogram, _ = np.histogram(gray_image.flatten(), bins=256, range=[0, 256])
# 计算每个像素值的概率
probabilities = histogram / float(np.sum(histogram))
# 计算信息熵
entropy = -np.sum(probabilities * np.log2(probabilities + np.finfo(float).eps))
return round(entropy,2)
2.4 熵增强(Extended maximum entropy,EME)
- 用于判断一幅图像中像素最大值和最小值之间的差别,即图像的对比度,值越大,对比度越好。
- 数学公式:

先将图像分为 k 1 × k 2 块,求出 先将图像分为k_{1}×k_{2}块,求出 先将图像分为k1?×k2?块,求出

2.5 平均梯度(Average gradient,AG)
- 反映图像的清晰度和纹理变化,数值越大说明图像越清晰。
- 数学公式:

其中, ? f ? x = I ( i + 1 , j ) ? I ( i , j ) , ? f ? y = I ( i , j + 1 ) ? I ( i , j ) 分别表示水平和垂直方向上的梯度 \frac{\partial f}{\partial x}=I(i+1,j)-I(i,j),\frac{\partial f}{\partial y}=I(i,j+1)-I(i,j) 分别表示水平和垂直方向上的梯度 ?x?f?=I(i+1,j)?I(i,j),?y?f?=I(i,j+1)?I(i,j)分别表示水平和垂直方向上的梯度 - 代码:
def AG(image):
# 将图像转换为灰度图像
image= cv2.normalize(image, None, 0, 255, cv2.NORM_MINMAX)
gray_image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
# 计算平均梯度
sobelx = cv2.Sobel(gray_image, cv2.CV_64F, 1, 0, ksize=3)
sobely =cv2.Sobel(gray_image, cv2.CV_64F, 0, 1, ksize=3)
AG = np.mean(np.sqrt(sobelx**2 + sobely**2))
return round(AG,2)
2.6 亮度顺序误差(LOE,lightness-order-error)
- 反映增强图像自然程度,其值越小,增强图像与原图像亮度顺序越接近,即自然度保持得越好。
- 数学公式:
对于每个像素 ( x , y ) (x,y) (x,y):

其中: R D ( x , y ) 表示相对亮度顺序差,计算公式为: RD(x,y)表示相对亮度顺序差,计算公式为: RD(x,y)表示相对亮度顺序差,计算公式为:

⊕ 表示异或操作 \oplus表示异或操作 ⊕表示异或操作, L e 和 L 分别为增强前后图片 L_{e}和L分别为增强前后图片 Le?和L分别为增强前后图片
U 的计算公式为: U的计算公式为: U的计算公式为:

L
(
x
,
y
)
表示
R
G
B
三通道中的最大值
L(x,y)表示RGB三通道中的最大值
L(x,y)表示RGB三通道中的最大值

- 实现代码:
def LOE(img,img_enhance):
H , W , C = img.shape
img= cv2.normalize(img, None, 0, 255, cv2.NORM_MINMAX)
img_enhance = cv2.normalize(img_enhance, None, 0, 255, cv2.NORM_MINMAX)
# 得到RGB通道中的最大值
L = np.max(img,axis = 2)
L_e = np.max(img_enhance,axis = 2)
# 计算相对亮度顺序差 RD
def RD(x,y):
mat = np.ones((H,W)) * L[x,y]
mat_en = np.ones((H,W)) * L_e[x,y]
res = np.bitwise_xor(np.where(mat >= L,1,0),np.where(mat_en >= L_e,1,0))
return np.sum(res)
# 计算亮度顺序误差 LOE
LOE = 0
for i in range(H):
for j in range(W):
LOE += RD(i,j)
LOE = round(LOE / (H*W),2)
return LOE
- 对于稍微大一点的图片,计算LOE的代码运算时间就会很长。代码如果有误或者可以给出改进,欢迎评论区交流。🧐
2.7 自然图像质量评价指标( N I Q E NIQE NIQE)
-
描述图像质量,其值越低,说明图像质量越高,越符合人眼的主观评价标准。
-
数学公式:
通过一个自然场景统计模型(NSS)进行质量特征提取,采用多元高斯模型(MVG)进行建模,将评估的图像质量表示为两者多元高斯分布之间的距离:
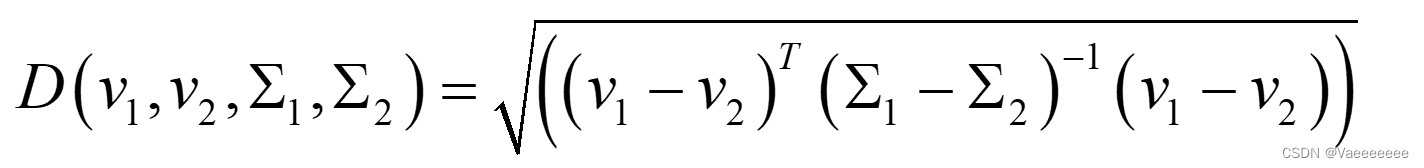
其中, v 1 , v 2 , ∑ 1 、 ∑ 2 分别表示 自然图像和失真图像的 M V G 模型均值和方差矩阵。 其中,v_{1},v_{2},\sum_{1}、\sum_{2}分别表示\\ 自然图像和失真图像的MVG模型均值和方差矩阵。 其中,v1?,v2?,∑1?、∑2?分别表示自然图像和失真图像的MVG模型均值和方差矩阵。 -
代码部分有点长,具体内容见主页资源。
总结
本文会长期更新内容,目前将平时常用的一些图像评价指标的代码附在了这里,争取将其他一些比较重要的评价标准写在一起,方便随时使用。🔍
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!