算法通关村第四关—表达式问题(黄金)

????????????表达式问题

一、计算器问题

?计算器也是非常常见的问题，我们看一个中等问题。LeetCode227.给你一个字符串表达式s，请你实现一个基本计算器来计算并返回它的值。整数除法仅保留整数部分。
?你可以假设给定的表达式总是有效的。所有中间结果将在[-231,231-1]的范围内。
?注意：不允许使用任何将字符串作为数学表达式计算的内置函数，比如eval()。
示例：

输入：s = "3+2*2"
输出：7

输入：s = " 3+5 / 2 " //注意有空格
输出：5

?解决运算器问题，最好的工具就是栈。由于乘除优先于加减计算，因此不妨考虑先进行所有乘除运算，并将这些乘除运算后的整数值放回原表达式的相应位置，则随后整个表达式的值，就等于一系列整数加减后的值。
?基于此，我们可以用一个栈，保存这些（进行乘除运算后的）整数的值。对于加减号后的数字，将其直接压入栈中；对于乘除号后的数字，可以直接与栈顶元素计算，并替换栈顶元素为计算后的结果。具体来说，遍历字符串s,并用变量preSign记录每个数字之前的运算符，对于第一个数字，其之前的运算符视为加号。每次遍历到数字未尾时，根据preSign来决定计算方式：
?加号：将数字压入栈；减号：将数字的相反数压入栈；乘除号：计算数字与栈顶元素，并将栈顶元素替换为计算结果。代码实现中，若读到一个运算符，或者遍历到字符串未尾，即认为是遍历到了数字末尾。处理完该数字后，更新preSign为当前遍历的字符。
?遍历完字符串s后，将栈中元素累加，即为该字符串表达式的值。

class Solution {
    public int calculate(String s) {
        Deque<Integer> stack = new LinkedList();
        int num = 0;
        char presign = '+';
        for(int i = 0; i < s.length(); i++){
            if(Character.isDigit(s.charAt(i))){
                num = num * 10 + (s.charAt(i) - '0');
            }
            if(i == s.length() - 1 || (!Character.isDigit(s.charAt(i)) && s.charAt(i) != ' ')){
                //四种情况可以考虑用switch
                if(presign == '+') stack.push(num);
                else if(presign == '-') stack.push(-1 * num);
                else if(presign == '*') stack.push(num * stack.pop());
                if(presign == '/') stack.push(stack.pop() / num);
                num = 0;
                presign = s.charAt(i);
            }
        }
        int sum = 0;
        while(stack.size() > 0){
            sum += stack.pop();
        }
        return sum;
    }
}

二、逆波兰表达式

?表达式计算是编译原理、自然语言处理、文本分析等领域非常重要的问题，我们这里看一个相对中等的问题，逆波兰表达式。LeetCode150.根据逆波兰表示法，求表达式的值。说明：
1.有效的算符包括+、一、*、/。每个运算对象可以是整数，也可以是另一个逆波兰表达式。
2.注意两个整数之间的除法只保留整数部分。
3.可以保证给定的逆波兰表达式总是有效的。也即表达式总会得出有效数值且不存在除数为0的情况。

?本题看起来很复杂，但其实很简单，我们先理解一下什么是表达式，表达式就是小学里学的类似（(2+1)*3)这样的式子，根据不同的记法，有前缀、中缀和后缀三种方式，其区别在于运算符相对于操作数的位置，前缀表达式的运算符位于操作数之前，中缀和后缀同理，如下图，其实这就对应了树的前中后三种遍历方式。

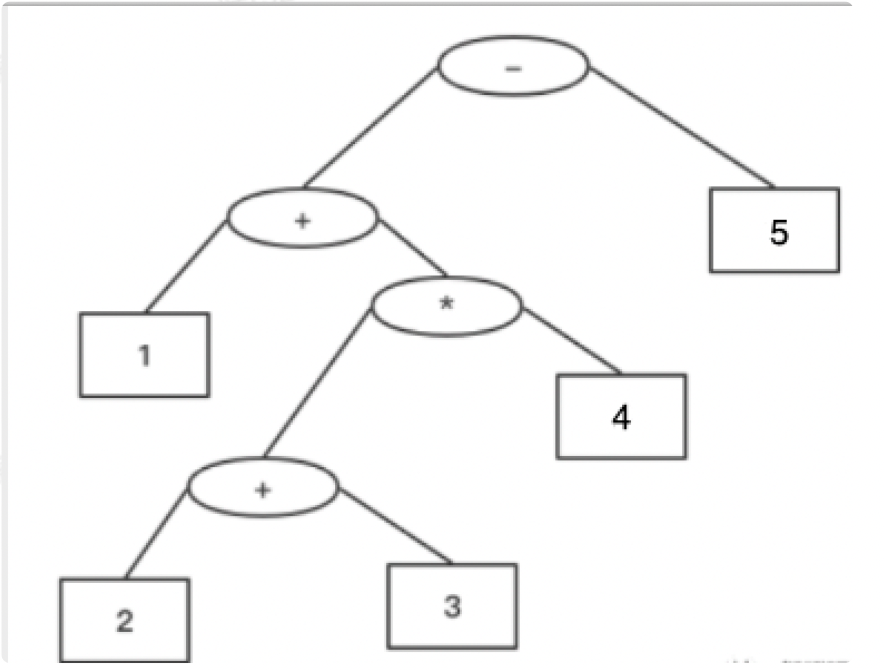
由上图推出下面三种表达式

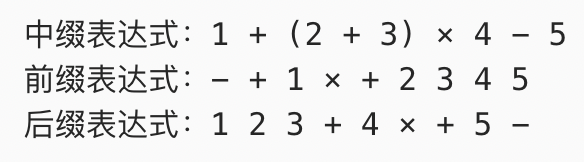
?中缀表达式是是一种通用的算术或逻辑公式表示方法，操作符以中缀形式处于操作数的中间。虽然人的大脑很容易理解与分析中缀表达式，但对计算机来说中缀表达式却是很复杂的，因此计算表达式的值时，通常需要先将中缀表达式转换为前缀或后缀表达式再进行求值。前缀表达式的运算符位于两个相应操作数之前，前缀表达式又被称为前缀记法或波兰式。而后缀式就是逆波兰式。
?观察后缀表达式可以发现，其特点就是数字先保存下来，然后遇到符号就计算，例如”123+“，遇到+号就将2+3加起来变成5再继续其他操作，直到最后完成。
?如果用栈来解释就是遇见数字即进栈，遇见运算符，则取出栈中最上面的两个元素进行计算，最后将运算结果入栈。实现代码其实很容易：

class Solution {
    public int evalRPN(String[] tokens) {
        Deque<Integer> stack = new LinkedList();
        for(int i = 0; i < tokens.length; i++){
            switch(tokens[i]){
                case "+":
                    stack.push(stack.pop() + stack.pop());
                    break;
                case "-":
                    int k = stack.pop();
                    stack.push(stack.pop() - k);
                    break;
                case "*":
                    stack.push(stack.pop() * stack.pop());
                    break;
                case "/":
                    int j = stack.pop();
                    stack.push(stack.pop() / j);
                    break;
                default:
                    int num = 0;
                    int judge = 1;
                    for(int n = 0; n < tokens[i].length(); n++){
                        if(tokens[i].charAt(n) == '-') judge = -1;
                        else num = num * 10 + (tokens[i].charAt(n) - '0');
                    }
                    stack.push(judge * num);
            }
        }
        return stack.pop();
    }
}