分治算法（三分快排 + 归并排序深入思维）万字

（阅读本文一定要具备二分快排的算法思维）将会直接从三分快排入手

基本思想

??分治算法（基于递归）将大问题分解成与原问题相似的子问题，递归地解决每个子问题，最后将子问题的解合并成大问题的解。分割的解法使得可以明显降低问题的复杂度。
??三分快排：对于二分快排的缺陷（元素全部相同排序）的优化时间复杂度为O(n)。???

引入算法题

??此处就是面对 二分快速排序 + 归并排序 的 深入 学习，如果只是想入门分治算法，那么掌握普通的 二分快速排序 + 归并排序 即可。

三分快排思维

颜色分类（三分快排入门必备）

链接: https://leetcode.cn/problems/sort-colors/

??给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ，原地对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。
??我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
??必须在不使用库内置的 sort 函数的情况下解决这个问题。

示例 1：
?输入：nums = [2,0,2,1,1,0]
?输出：[0,0,1,1,2,2]

题目分析：

??此题是 移动零 的double版本，属于三指针，三指针与双指针一样都是区域的划分问题。移动零(双指针讲解)。

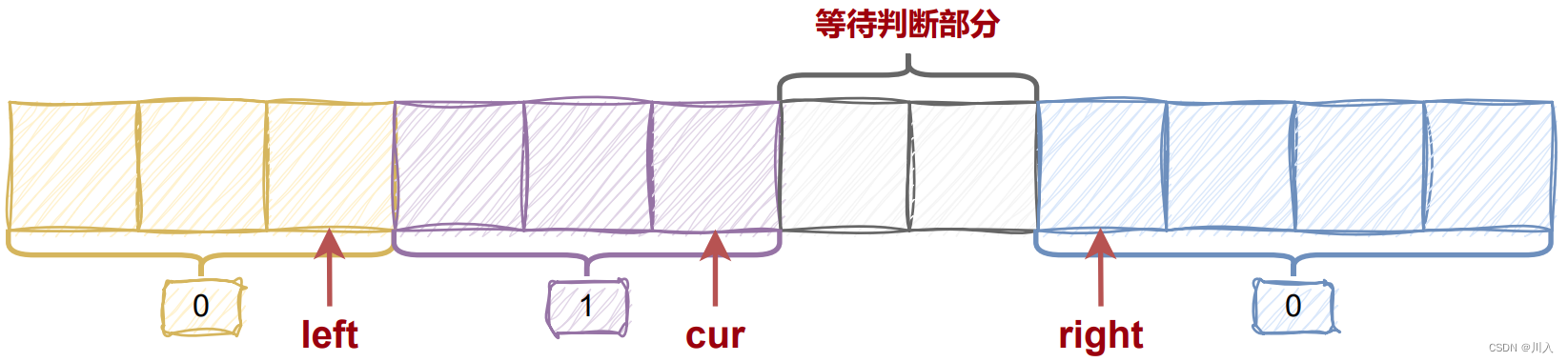
解题：

• 三指针：
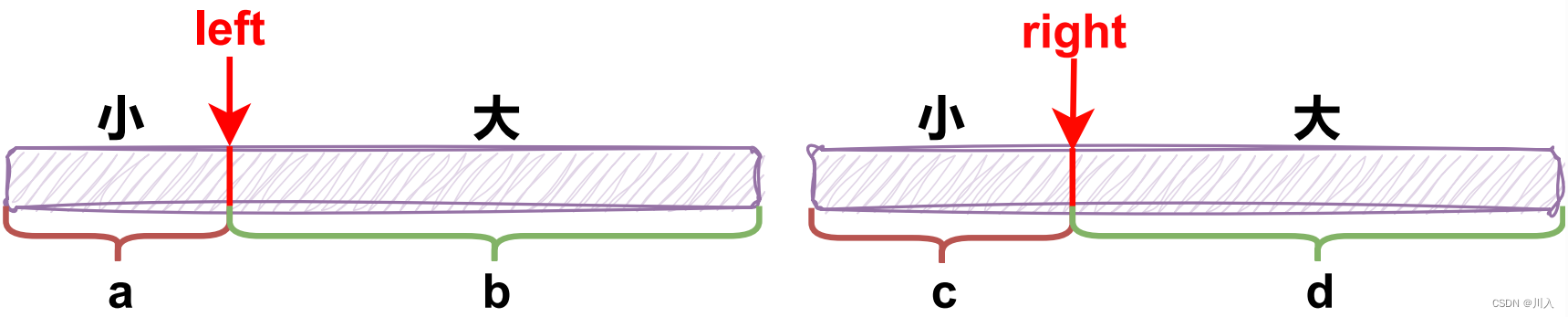
• cur：遍历数组。
• left：标记 0 区域的最右侧。
• right：标记 2 区域的最左侧。
• 区域划分：
• [0, left]：全是 0 。
• [left + 1, cur - 1]：全是 1 。
• [cur, right - 1]：待判断。
• [right, nums.size() - 1]：全是 2 。

class Solution {
public:
    void sortColors(vector<int>& nums) {
        int cur = 0, left = -1, right = nums.size();
        while(cur < right)
        {
            if(nums[cur] == 0)
                swap(nums[++left], nums[cur++]);
            else if(nums[cur] == 1)
                cur++;
            else
                // 此处cur并不能++，因为right - 1并未被判断
                swap(nums[--right], nums[cur]);
        }
    }
};

三分快排

链接: https://leetcode.cn/problems/sort-an-array/description/

??给你一个整数数组 nums，请你将该数组升序排列。

示例 1：
?输入：nums = [5,2,3,1]
?输出：[1,2,3,5]

题目分析：

??就是可能存在大量数据重复的排序题，所以需要使用到三分快排。

解题：

• 用随机方式选基准元素
  ??优化：用随机方式选择基准元素的（必要性）《算法导论》中通过概率求期望，时间复杂度可以渐进到 $NlogN$（对于二分快排）。

class Solution {
public:
    vector<int> sortArray(vector<int>& nums) {
        srand(time(NULL));
        quick_sort(nums, 0, nums.size() - 1);
        return nums;
    }

    void quick_sort(vector<int>& nums, int prev, int tail)
    {
        if(prev >= tail)  // 有可能出现如没有<的值，于是tail = left = -1
            return;
		// 数组分三块
        int key = nums[rand_num(prev, tail)];
        int left = prev - 1, right = tail + 1;
        int cur = prev;
        while(cur < right)
        {
            if(nums[cur] < key)
                swap(nums[++left], nums[cur++]);
            else if(nums[cur] == key)
                cur++;
            else
                swap(nums[--right], nums[cur]);
        }

		// [prev, left](<)  [left + 1, right - 1](==)  [right, tail](>)
        quick_sort(nums, prev, left);
        quick_sort(nums, right, tail);
    }

    int rand_num(int prev, int tail)
    {
        int r = rand();
        return r % (tail - prev + 1) + prev;
    }
};

初步识别思路???

• 对于一个nums数组，三分快排会将数据分割为 [<key][=key][>key] or [>key][=key][<key] ，所以其是比二分快排分割更有性价比的，可以通过此分割实现数据分割看待。

数组中的第K个最大元素

链接: https://leetcode.cn/problems/kth-largest-element-in-an-array/description/

??给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。
??请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。
??你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。

示例 1:
?输入: [3,2,1,5,6,4], k = 2
?输出: 5

题目分析：

??此处要求时间复杂度为O($N$)，所以正常的堆排（时间复杂度O($NlogN$)）已经无法解决这个问题。而三分快排的方式可以使用O($N$)的时间找到，《算法导论》有严格的证明。

解题：

• 状态划分：题需要第 k 大。
  1、c >= k $\to$ 去[right, tail]查找第 k 个。
  2、b + c >= k $\to$ 返回。
  3、b + c < k $\to$ 去[prev, left]查找第 k - b - c 个。

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        srand(time(nullptr));
        q_sort(nums, 0, nums.size() - 1, k);
        return nums[nums.size() - k];
    }

    void q_sort(vector<int>& nums, int prev, int tail, int k)
    {
        if(prev >= tail)
            return;

        int key = nums[rand_num(prev, tail)];
        int left = prev - 1, right = tail + 1;
        int cur = prev;
        while(cur < right)
        {
            if(nums[cur] < key)
                swap(nums[++left], nums[cur++]);
            else if(nums[cur] == key)
                cur++;
            else
                swap(nums[--right], nums[cur]);
        }

        // 判断第k大属于哪个区域
        int b = right - left - 1, c = tail - right + 1;
        if(k <= c)
            q_sort(nums, right, tail, k);
        else if(k <= b + c)
            return;
        else
            q_sort(nums, prev, left, k - b - c);
    }

    int rand_num(int prev, int tail)
    {
        return rand() % (tail - prev + 1) + prev;
    }
};

库存管理 III

链接: https://leetcode.cn/problems/zui-xiao-de-kge-shu-lcof/description/

??仓库管理员以数组 stock 形式记录商品库存表，其中 stock[i] 表示对应商品库存余量。请返回库存余量最少的 cnt 个商品余量，返回 顺序不限。

示例 1：
?输入：stock = [2,5,7,4], cnt = 1
?输出：[2]

题目分析：

??不多说了，就是上一题的升级，进一步不是 第K大/小，而是 K大/小 。

解题：

• 状态划分：题需要 k 小。
  1、a > k $\to$ 去[prev, left]查找 k 个。
  2、a + b >= k $\to$ 返回。
  3、a + b < k $\to$ 去[right, tail]查找 k - a - b 个。

class Solution {
public:
    vector<int> inventoryManagement(vector<int>& stock, int cnt) {
        srand(time(nullptr));
        q_sort(stock, 0, stock.size() - 1, cnt);
        return {stock.begin(), stock.begin() + cnt};
    }

    void q_sort(vector<int>& nums, int prev, int tail, int cnt)
    {
        if(prev >= tail)
            return;

        int key = nums[rand_num(prev, tail)];
        int left = prev - 1, right = tail + 1;
        int cur = prev;
        while(cur < right)
        {
            if(nums[cur] < key)
                swap(nums[++left], nums[cur++]);
            else if(nums[cur] == key)
                cur++;
            else
                swap(nums[--right], nums[cur]);
        }

        // 判断最小的cnt个属于哪个区域
        int a = left + 1 - prev, b = right - left - 1;
        if(a > cnt)
            q_sort(nums, prev, left, cnt);
        else if(a + b >= cnt)
            return;
        else
            q_sort(nums, right, tail, cnt - a - b);
    }

    int rand_num(int prev, int tail)
    {
        return rand() % (tail - prev + 1) + prev;
    }
};

归并排序思维

初步识别思路???

• 对于一个nums数组，以前后关系所对应的数量类似的要求，就可以尝试使用归并排序时：「左半部分排序」+「右半部分排序」= 上个递归的「左半部分排序」or「右半部分排序」的特性，完成排序时分析，实现 O($NlongN$) 重合归并排序的时间复杂度。
• 根据分析：无需现在看懂，此处是后续题的总结，直接看题即可。

注意： 看似一摸一样，就是换一个方向，但是从程序员的角度，如此调换截然不同！！！

• 策略一：计算当前元素后面，有多少元素的比我小nums[left] > nums[right]，右部分个数 - 降序重点降序，需求[left] > [right, 最后]。
  
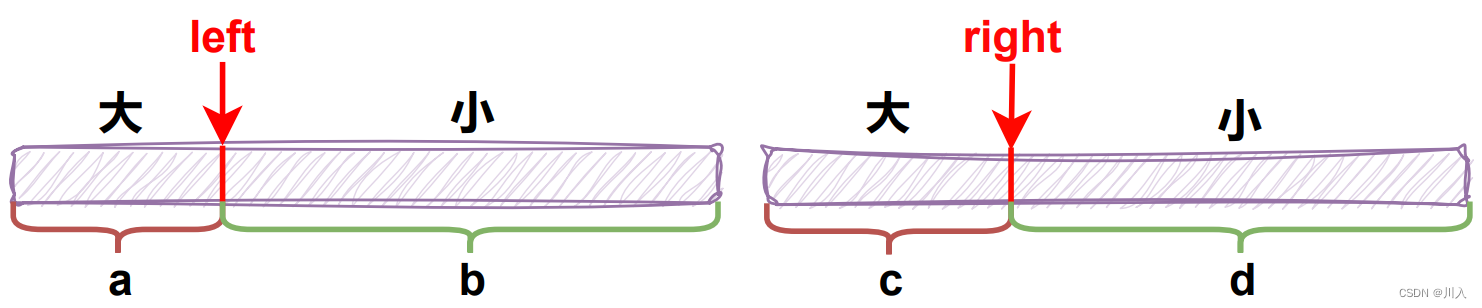
• 策略二：计算当前元素之前，有多少元素的比我大nums[right] < nums[left]，左部分个数 - 升序重点升序，需求[i, mid] > [j]。
  

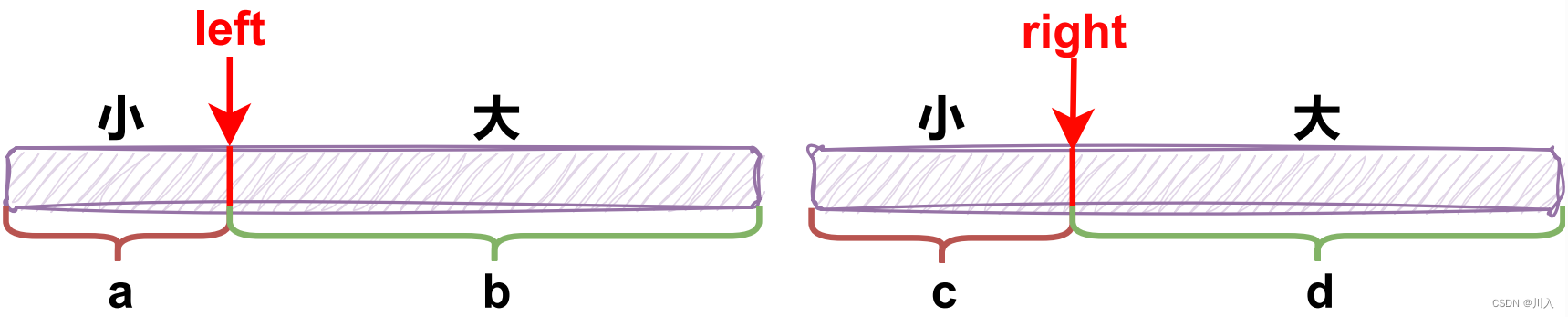
归并排序

链接: https://leetcode.cn/problems/sort-an-array/description/

??给你一个整数数组 nums，请你将该数组升序排列。

示例 1：
?输入：nums = [5,2,3,1]
?输出：[1,2,3,5]

题目分析：

??这就是前面三分快排所解的题，此处目的是再写一遍归并排序的算法。

解题：

• 归并排序的流程充分的体现了「分而治之」的思想：
  • 分：将数组?分为?为两部分，?直分解到数组的长度为 1 ，使整个数组的排序过程被分为「左半部分排序」 + 「右半部分排序」。
  • 治：将两个较短的「有序数组合并成?个长的有序数组」，?直合并到最初的长度。

class Solution {
    vector<int> tmp;
public:
    vector<int> sortArray(vector<int>& nums) {
        int size = nums.size();
        tmp.resize(size);
        merge_sort(nums, 0, size - 1);
        return nums;
    }

    void merge_sort(vector<int>& nums, int prev, int tail)
    {
        if(prev >= tail)
            return;

        int mid = prev + ((tail - prev) >> 1);

        // 进行递归
        merge_sort(nums, prev, mid);
        merge_sort(nums, mid + 1, tail);

        // 进行排序
        int left = prev, right = mid + 1;
        int i = 0; // tmp的映射位置
        while(left <= mid && right <= tail)
        {
            tmp[i++] = nums[left] <= nums[right] ? nums[left++] : nums[right++];
        }
        // 将数据遍历完
        while(left <= mid) tmp[i++] = nums[left++];
        while(right <= tail) tmp[i++] = nums[right++];

        // 还原
        for(int i = prev; i <= tail; i++)
            nums[i] = tmp[i - prev];
    }
};

交易逆序对的总数

链接: https://leetcode.cn/problems/shu-zu-zhong-de-ni-xu-dui-lcof/description/

??在股票交易中，如果前一天的股价高于后一天的股价，则可以认为存在一个「交易逆序对」。请设计一个程序，输入一段时间内的股票交易记录 record，返回其中存在的「交易逆序对」总数。

示例 1:
?输入：record = [9, 7, 5, 4, 6]
?输出：8
?解释：交易中的逆序对为 (9, 7), (9, 5), (9, 4), (9, 6), (7, 5), (7, 4), (7, 6), (5, 4)。

题目分析：

??此题，如果用暴力解题的方法找逆序对，那么就是两层for循环，时间复杂度O($N^2$)。此题最好的方式是采用归并排序的特性来解决，达到时间复杂度O($logN$)。

注意： 需要的是前者 > 后者，并不是一大一小任意组合！！！

解题：

• 归并排序能够保证在一层递归中的左右子数组是有序的！
  

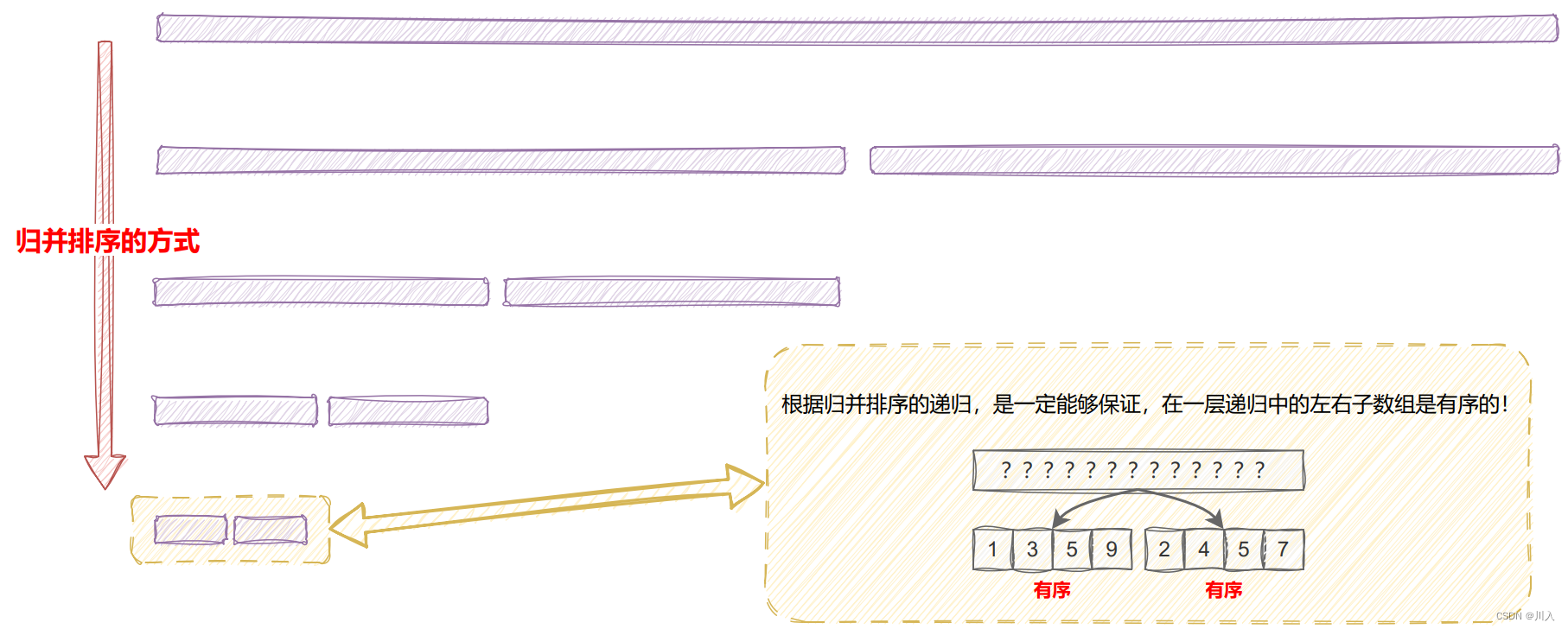
??当我们确定，左右子数组其自身一定是有序的，于是便可以评定此特性求解，达到解题时间复杂度与归并排序的时间复杂度所重合。

??我们需要明确一个点， a 与 c 两个段的所有数据一定是小于 b 与 d 两个段的所有数据。（如果想不清一定需要明确：一层递归中左右子数组其自身一定是有序的）

• 场景模拟（此时：按升序排序）
  • nums[left] <= nums[right]
    • 此时left++;，因为我们渴望[left, mid] > [right]的数据，此处明显不符合。
  • nums[left] > nums[right]
    • 此时ret += mid - left + 1; right++;，这就是渴望的[left, mid] > [right]的数据，此时就能够知道 右取一个数据 与 左取一个数据 能组成的一共的逆序对个数。

??此处如果对于分治算法（归并排序）掌握完全此处就已经是解答。

但：提到的都是 `右取一个数据` 与 `左取一个数据` 组成的，右部分的组成 / 左部分的组成就不算了吗？

??这就是分治算法的特性，此处的右部分的组成 / 左部分的组成，在上一个递归不还是
右取一个数据 与 左取一个数据 组成的吗？所以看似需要求整体的话是：左部分的逆序对 + 右部分的逆序对 + 左右各取一个的逆序对 == 左右各取一个的逆序对（真正实际需要的！）。

思考升级： 此处使用的是利用归并排序升序，如果是降序呢？ （会在升序后给出解答，建议进行尝试）

• 将代码文字化
• 定义递归出口： left >= right 时，直接返回；
• 划分区间： 根据中点 mid，将区间划分为 [prev, mid] 和 [mid + 1, tail]；
• 统计左右两个区间逆序对的数量：（此处就是递归到下一层递归，求该区间分半之后的左右各取一个的逆序对）
  • 统计左边区间 [prev, mid] 中每个元素对应的逆序对的数量到 ret 中，并排序；
  • 统计右边区间 [mid + 1, tail] 中每个元素对应的逆序对的数量到 ret 中，并排序。
• 合并左右两个有序区间，并且统计出逆序对的数量：
  • 辅助数组：tmp。
  • 初始化遍历数组的指针：left = prev（遍历左半部分数组）right = mid + 1（遍历右半边数
    组）ret = 0（逆序对数量）
  • 循环合并区间：
    • nums[left] <= nums[right]
      • 此时left++;。
    • nums[left] > nums[right]
      • 此时ret += mid - left + 1; right++;。
  • 将辅助数组的内容替换到原数组中去；

class Solution {
    vector<int> tmp;
    int ret = 0;
public:
    int reversePairs(vector<int>& record) {
        tmp.resize(record.size());
        merge_sort(record, 0, record.size() - 1);
        return ret;
    }

    void merge_sort(vector<int>& nums, int prev, int tail)
    {
        if(prev >= tail)
            return;
        
        int mid = prev + ((tail - prev) >> 1);

        // 进行递归
        merge_sort(nums, prev, mid);
        merge_sort(nums, mid + 1, tail);

        // 进行排序 + 计算逆序对 - 升序
        int left = prev, right = mid + 1;
        int i = 0;
        while(left <= mid && right <= tail)
        {
            if(nums[left] <= nums[right])
                tmp[i++] = nums[left++];
            else
            {
                ret += mid - left + 1;
                tmp[i++] = nums[right++];
            }
        }

        while(left <= mid) tmp[i++] = nums[left++];
        while(right <= tail) tmp[i++] = nums[right++];

        // 归还数据
        for(int i = prev; i <= tail; i++)
        {
            nums[i] = tmp[i - prev];
        }
    }
};

#： 归并排序 降序

??需要明确一个点，以升序为例：我们是让一个数据和一个区域相组合，那么我们就需要保证，组合计算过后的那单一数据必须移动，不然就会出现重复逆序对。

• 以升序易错的错例为例：
  
  • nums[left] < nums[right]
    • 此时ret += mid - left + 1; left++;
  • nums[left] >= nums[right]
    • 此时right++;

??看似是可以的，当nums[left] < nums[right]时能够使得 [头, left] < [right] 进行逆序对的组合，但是 小大 组合，并不是 大小 组合的逆序对。而且逻辑上万一同样的nums[left + 1] < nums[right]，那么就会 [头, left + 1] < [right] 进行组合，导致[头, left]被计算两次，也是不行的。

• 降序的正确做法
  
• 场景模拟（此时：按降序排序）
  • nums[left] <= nums[right]
    • 此时right++;，因为我们渴望[left] > [right, tail]的数据，此处明显不符合。
  • nums[left] > nums[right]
    • 此时ret += tail - right + 1; left++;，这就是渴望的[left] > [right, tail]的数据，此时就能够知道 右取一个数据 与 左取一个数据 能组成的一共的逆序对个数。

class Solution {
    vector<int> tmp;
public:
    int reversePairs(vector<int>& record) {
        tmp.resize(record.size());
        return merge_sort(record, 0, record.size() - 1);
    }
    int merge_sort(vector<int>& nums, int prev, int tail)
    {
        int ret = 0;
        if(prev >= tail)
            return 0;

        int mid = prev + ((tail - prev) >> 1);

        ret += merge_sort(nums, prev, mid);
        ret += merge_sort(nums, mid + 1, tail);

        int i = 0;
        int left = prev, right = mid + 1;
        // 降序版本
        while(left <= mid && right <= tail)
        {
            if(nums[left] <= nums[right])
            {
                tmp[i++] = nums[right++];
            }
            else if(nums[left] > nums[right])
            {
                ret += tail - right + 1;
                tmp[i++] = nums[left++];
            }
        }
        while(left <= mid) tmp[i++] = nums[left++];
        while(right <= tail) tmp[i++] = nums[right++];
        for(int j = prev; j <= tail; j++)
            nums[j] = tmp[j - prev];

        return ret;
    }
};

总结：

• 策略一： 左侧有多少值，比右侧定值大 - 升序。
• 策略二： 右侧有多少值，比左侧定值小 - 降序。

计算右侧小于当前元素的个数

链接: https://leetcode.cn/problems/count-of-smaller-numbers-after-self/description/

??给你一个整数数组 nums ，按要求返回一个新数组 counts 。数组 counts 有该性质： counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。

示例 1：
?输入：nums = [5,2,6,1]
?输出：[2,1,1,0]
?解释：
?5 的右侧有 2 个更小的元素 (2 和 1)
?2 的右侧仅有 1 个更小的元素 (1)
?6 的右侧有 1 个更小的元素 (1)
?1 的右侧有 0 个更小的元素

题目分析：

??此题看似困难，但其实就是上题的策略之一：策略二： 右侧有多少值，比左侧定值小 - 降序。

解题：

• 此题重点
  与上题区别，就是需要根据 nums数组中数据的原始下标进行记录：右侧有多少值，比左侧定值小。
  同理，也就是如使用 nums + tmp_nums组合 一样，为原始下标记录也配一个 tmp_index + index组合 。

class Solution {
    vector<int> tmp_nums;
    vector<int> index;
    vector<int> tmp_index;

public:
    vector<int> countSmaller(vector<int>& nums) {
        int n = nums.size();
        tmp_nums.resize(n);
        index.resize(n);
        tmp_index.resize(n);

        // 记录下标
        for(int i = 0; i < n; i++)
            index[i] = i;

        // 返回数组
        vector<int> ret;
        ret.resize(n);

        // 归并排序解题
        merge(nums, 0, n - 1, ret);

        return ret;
    }

    void merge(vector<int>& nums, int prev, int tail, vector<int>& ret)
    {
        if(prev >= tail)
            return;
        
        int mid = prev + ((tail - prev) >> 1);
        merge(nums, prev, mid, ret);
        merge(nums, mid + 1, tail, ret);

        int i = 0;
        int left = prev, right = mid + 1;

        // 降序解题
        while(left <= mid && right <= tail)
        {
            if(nums[left] <= nums[right])
            {
                tmp_nums[i] = nums[right];
                tmp_index[i++] = index[right++];
            }
            else
            {
                ret[index[left]] += tail - right + 1;
                tmp_nums[i] = nums[left];
                tmp_index[i++] = index[left++];
            }
        }
        while(left <= mid)
        {
            tmp_nums[i] = nums[left];
            tmp_index[i++] = index[left++];
        }
        while(right <= tail)
        {
            tmp_nums[i] = nums[right];
            tmp_index[i++] = index[right++];
        }

        for(int j = prev; j <= tail; j++)
        {
            nums[j] = tmp_nums[j - prev];
            index[j] = tmp_index[j - prev];
        }
    }
};

翻转对

链接: https://leetcode.cn/problems/reverse-pairs/description/

??给定一个数组 nums ，如果 i < j 且 nums[i] > 2*nums[j] 我们就将 (i, j) 称作一个重要翻转对。
??你需要返回给定数组中的重要翻转对的数量。

示例 1:
?输入: [1,3,2,3,1]
?输出: 2

题目分析：
??此题与逆序对极其相似，只不过一个是i<j && nums[i] > 2*nums[j]，另一个是i<j && nums[i] > nums[j]。
解题：
??前面的题如：逆序对，是因为比较的值是一对一的，所以能与归并排序所完美的结合。而此处需要的是 i<j && nums[i] > 2*nums[j] ，是无保证 [left] > [right, tail] && 一定符合 nums[left] > 2*nums[right] 。所以其是无法与归并排序进行重合，需要提前计算。
??可以达到一次递归，提前计算的重要翻转对数量时间复杂度为O($N$)。

• 根据分析：
• 策略一：计算当前元素后面，有多少元素的两倍比我小nums[i] > 2*nums[j] - 降序。
• 策略二：计算当前元素之前，有多少元素的一半比我大nums[j] < nums[i] / 2.0 - 升序。

注意： 看似一摸一样，就是换一个方向，但是从程序员的角度，如此调换截然不同！！！

??通过前一步的分析，我们可以知道，之所以其无法与归并排序所完美的结合，就是因为其不是如i<j && nums[i] > 2*nums[j]的数据对应，所以重点是改变的一方对应的范围。

• nums[i] > 2*nums[j]的重点是> 2*nums[j]，就是右半部分，所以需要右半部分越来越小 - 降序。
• nums[j] < nums[i] / 2.0的重点是< nums[i] / 2.0，就是左半部分，所以需要左半部分越来越大 - 升序。

说白了就是：利用单调性，以递增 / 递减，使用「相向双指针」来解决 - 不回退，同时向一个方向进行移动。

策略一：利用降序排序

class Solution {
    vector<int> tmp;

public:
    int reversePairs(vector<int>& nums) {
        tmp.resize(nums.size());

        return merge(nums, 0, nums.size() - 1);
    }

    int merge(vector<int>& nums, int prev, int tail)
    {
        if(prev >= tail)
            return 0;
        
        int ret = 0;
        int mid = prev + ((tail - prev) >> 1 );

        ret += merge(nums, prev, mid);
        ret += merge(nums, mid + 1, tail);

        int i = 0;
        int left = prev, right = mid + 1;

        // 计算重要翻转对 - 降序排序 - 对应 > nums[j] * 2 - 关注：右半部分
        int i_left = left, j_right = right;
        while(i_left <= mid)
        {
            while(j_right <= tail && nums[i_left] <= (long long)2 * nums[j_right])
            {
                j_right++;
            }
            if(i_left > mid)
                break;
            ret += tail - j_right + 1;
            i_left++;
        }

        // 降序排序 - 对应 > nums[j] * 2
        while(left <= mid && right <= tail)
        {
            if(nums[left] <= nums[right])
                tmp[i++] = nums[right++];
            else
                tmp[i++] = nums[left++];
        }

        while(left <= mid) tmp[i++] = nums[left++];
        while(right <= tail) tmp[i++] = nums[right++];
        for(int i = prev; i <= tail; i++)
            nums[i] = tmp[i - prev];

        return ret;
    }
};

策略二：利用升序排序

class Solution {
    vector<int> tmp;

public:
    int reversePairs(vector<int>& nums) {
        tmp.resize(nums.size());

        return merge(nums, 0, nums.size() - 1);
    }

    int merge(vector<int>& nums, int prev, int tail)
    {
        if(prev >= tail)
            return 0;
        
        int ret = 0;
        int mid = prev + ((tail - prev) >> 1 );

        ret += merge(nums, prev, mid);
        ret += merge(nums, mid + 1, tail);

        int i = 0;
        int left = prev, right = mid + 1;

        // 计算重要翻转对 - 升序排序 - 对应 < nums[i] / 2.0 - 关注：左半部分
        int i_left = left, j_right = right;
        while(j_right <= tail)
        {
            while(i_left <= mid && nums[j_right] >= nums[i_left] / 2.0)
            {
                i_left++;
            }
            if(i_left > mid)
                break;
            ret += mid - i_left + 1;
            j_right++;
        }

        // 升序排序 - 对应 < nums[i] / 2.0
        while(left <= mid && right <= tail)
        {
            if(nums[left] >= nums[right])
                tmp[i++] = nums[right++];
            else
                tmp[i++] = nums[left++];
        }

        while(left <= mid) tmp[i++] = nums[left++];
        while(right <= tail) tmp[i++] = nums[right++];
        for(int i = prev; i <= tail; i++)
            nums[i] = tmp[i - prev];

        return ret;
    }
};