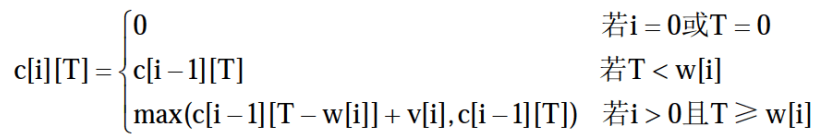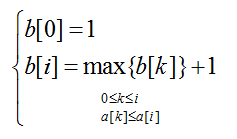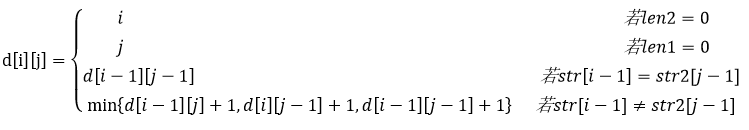软件设计师笔记——(第八章:算法设计与分析)
目录
一、历年真题总结

二、回溯法(???)
1、N皇后(回溯法)(19上)
1.回溯思想(一般用于解决迷宫类的问题)

?此图来自AC中的Hasity作者,万分感谢;(海绵宝宝tql)
- 1.判断是否在同一列上面。
- 2.判断是否在同一斜线上(斜率的绝对值是否相同)。
- 3.依次进行递归+回溯,知道满足判断跳出条件。
- 4.可以借鉴此篇博客了解学习DFS:http://t.csdnimg.cn/moPrF
2.题目描述(19下原题)
皇后问题描述为:在一个的棋盘上摆放个皇后,要求任意两个皇后不能冲突,
即任意两个皇后不在同一行、同一列或者同一斜线上。
算法的基本思想如下:
将第个皇后摆放在第行,从1开始,每个皇后都从第1列开始尝试。尝试时判断在该列摆放皇后是否与前面的皇后有冲突,
如果没有冲突,则在该列摆放皇后,并考虑摆放下一个皇后;
如果有冲突,则考虑下一列。如果该行没有合适的位置,回溯到上一个皇后,
考虑在原来位置的下一个位置上继续尝试摆放皇后……直到找到所有合理摆放方案。
【C代码】常量和变量说明
n:皇后数,棋盘规模为n×n。
queen[]:皇后的摆放位置数组,queen[i]表示第i个皇后的位置。
#include <stdio.h>
#define n 4
int queen[n + 1];
void Show() { /* 输出所有皇后摆放方案 */
int i;
printf("(");
for (i = 1; i <= n; i++) {
printf(" %d", queen[i]);
}
printf(")\n");
}
int Place(int j) {/* 检查当前列能否放置皇后,不能放返回0,能放返回1 */
int i;
for (i = 1; i < j; i++) { /*检查与已摆放的皇后是否在同一列或者同一斜线上*/
if ((1) || abs(queen[i] - queen[j]) == (j - i)) {
return 0;
}
}
return (2);
}
void Nqueen(int j) {
int i;
for (i = 1; i <= n; i++) {
queen[j] = i;
if ((3)) {
if (j == n) { /* 如果所有皇后都摆放好,则输出当前摆放方案 */
Show();
}
else { /* 否则继续摆放下一个皇后 */
(4);
}
}
}
}
int main() {
Nqueen(1);
return 0;
}
#【问题1】(8分)
根据题干说明,填充C代码中的空(1)~(4)。
#【问题2】(3分)
根据题干说明和C代码,算法采用的设计策略为(5) ?
#【问题3】(4分)
当n = 4时,有 ?(6) ?种摆放方式,分别为(7)
2、N皇后(循环法)(15上)
n-皇后问题是在n行n列的棋盘上放置n个皇后,使得皇后彼此之间不受攻击,
其规则是任意两个皇后不在同一行、同一列和相同的对角线上。
算法的基本思想如下:
拟采用以下思路解决n-皇后问题:第i个皇后放在第i行。从第一个皇后开始,对每个皇后,从其对应行(第i个皇后对应第i行)
的第一列开始尝试放置,若可以放置,确定该位置,考虑下一个皇后;
若与之前的皇后冲突,则考虑下一列;
若超出最后一列,则重新确定上一个皇后的位置。
重复该过程,直到找到所有的放置方案。
【C代码】常量和变量说明
pos:一维数组,pos[i]表示第i个皇后放置在第i行的具体位置
count:统计放置方案数
i,j,k:变量
N:皇后数
#include <stdio.h>
#include <math.h>
#define N 10
/* 判断第k个皇后目前放置位置是否与前面的皇后冲突 */
int isplace(int pos[], int k) {
int i;
for(i = 1; i < k; i ++ )
if ((1) || fabs(i - k) == fabs(pos[i] - pos[k]))
return 0;
return 1;
}
int main() {
int i, j, count = 1;
int pos[N + 1];
// 初始化位置
for (i = 1; i <= N; i ++ )
pos[i] = 0;
(2);
while (j >= 1) {
pos[j] = pos[j] + 1;
/* 尝试摆放第 j 个皇后 */
while (pos[j] <= N && (3)) {
pos[j] = pos[j] + 1;
}
/* 得到一个摆放方案 */
if (pos[j] <= N && j == N) {
printf("方案%d:", count ++ );
for (i = 1; i <= N; i ++ )
printf("%d", pos[i]);
printf("\n");
}
/* 考虑下一个皇后 */
if (pos[j] <= N && (4)) {
j = j + 1;
} else { // 返回考虑上一个皇后
pos[j] = 0;
(5);
}
}
return 1;
}
【问题1】(10分)
根据以上说明和C代码,填充C代码中的空(1)?(5)。
【问题2】(2分)
根据以上说明和C代码,算法采用了 (6) 设计策略。
【问题3】(3分)
上述C代码的输出为: (7) 3、深度优先(17下)
一个无向连通图G点上的哈密尔顿(Hamilton)回路是指从图G上的某个顶点出发
经过图上所有其他顶点一次且仅一次,最后回到该顶点的路径。
算法的基本思想如下:
假设图G存在一个从顶点出发的哈密尔顿回路。算法从顶点出发,访问该顶点的一个未被访问的邻接顶点,
接着从顶点出发,访问一个未被访问的邻接顶点,
对顶点,重复进行以下操作:访问的一个未被访问的邻接接点;
若的所有邻接顶点均已被访问,则返回到顶点,
考虑的下一个未被访问的邻接顶点,仍记为;
直到找到一条哈密尔顿回路或者找不到哈密尔顿回路,算法结束。
【C代码】常量和变量说明
n:图G中的顶点数
c[][]:图G的邻接矩阵
k:统计变量,当前已经访问的顶点数为k + 1
x[k]:第k个访问的顶点编号,从0开始
visited[x[k]]:第k个顶点的访问标志,0表示未访问,1表示已访问
#include <stdlib.h>
#define MAX 100
void Hamilton(int n, int x[MAX], int c[MAX][MAX]) {
int i;
int visited[MAX];
int k;
for (i = 0; i < n; i++) {
/
x[i] = 0;
visited[i] = 0;
}/* 访问起始顶点 */
k = 0;
(1);
x[0] = 0;
k = k + 1;
while (k >= 0) {/* 访问其他顶点 */
x[k] = x[k] + 1;
while (x[k] < n) {
/* 邻接顶点x[k]未被访问过 */
if ((2) && c[x[k - 1]][x[k]] == 1) {
break;
}
else {
x[k] = x[k] + 1;
}
}
if (x[k] < n && k == n - 1 && (3)) { /* 找到一条哈密尔顿回路 */
for (k = 0; k < n; k++) {
printf("%d--", x[k]); /* 输出哈密尔顿回路 */
}
printf("%d\n", x[0]);
return;
/* 设置当前顶点的访问标志,继续下一个顶点 */
}
else if (x[k] < n && k < n - 1) {
(4);
k = k + 1;
}
else { /* 没有未被访问过的邻接顶点,回退到上一个顶点 */
x[k] = 0;
visited[x[k]] = 0;
(5);
}
}
}
【问题1】(10分)
根据题干说明。填充C代码中的空(1)~(5)。
【问题2】(5分)
根据题干说明和C代码,算法采用的设计策略为(6),
该方法在遍历图的顶点时,采用的是(7)方法(深度优先或广度优先)。三、分治法(???)
1、归并排序(14上)
1.算法处理
归并排序,它有两大核心操作:
- 一个是将数组一分为二,一个无序的数组成为两个数组。
- 另外一个操作就是,合二为一,将两个有序数组合并成为一个有序数组。
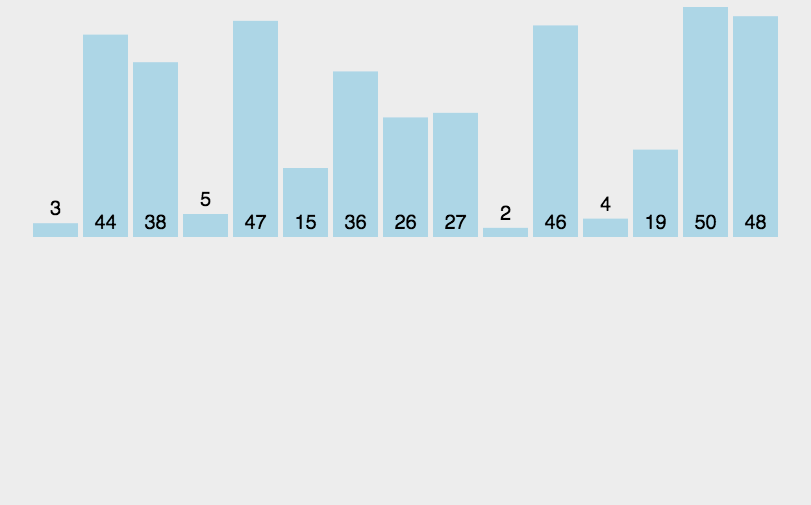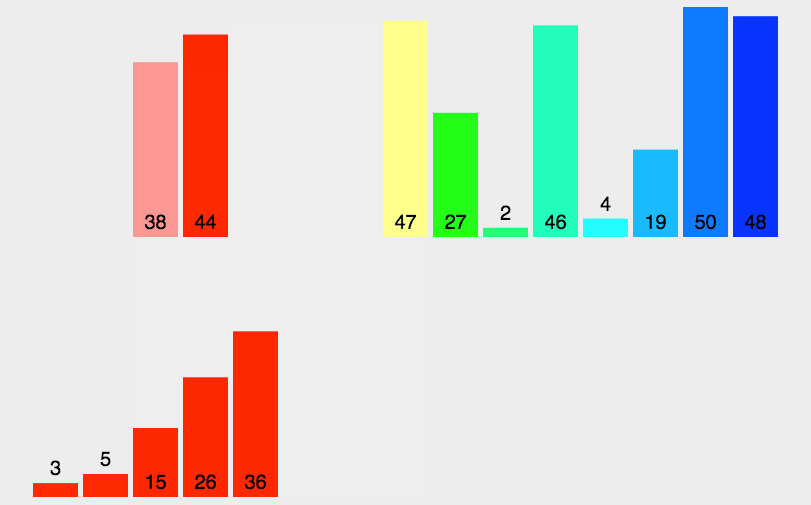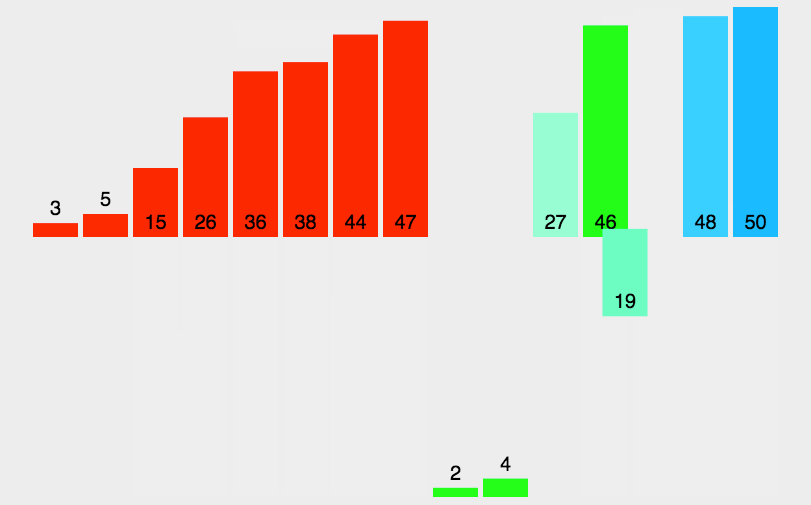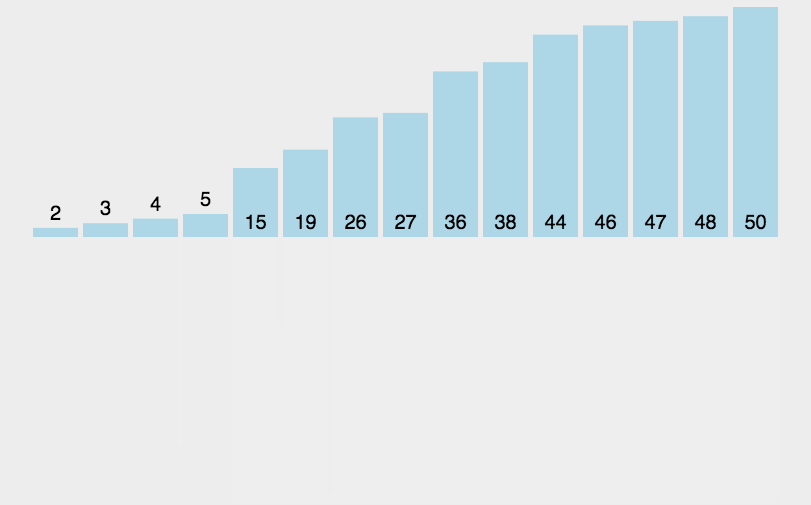
2.题目描述
采用归并排序对n个元素进行递增排序时,
首先将n个元素的数组分成各含n/2个元素的两个子数组,
然后用归并排序对两个子数组进行递归排序,
最后合并两个已经排好序的子数组得到排序结果。
【C代码】常量和变量说明
arr:待排序数组
p,q,r:一个子数组的位置为从p到q,另一个子数组的位置为从q+1到r
begin,end:待排序数组的起止位置
left,right:临时存放待合并的两个子数组
n1,n2:两个子数组的长度
i,j,k:循环变量
mid:临时变量
#include <stdio.h>
#include <stdlib.h>
#define MAX 65536
void merge(int arr[], int p, int q, int r) {
int *left, *right;
int n1, n2, i, j, k;
n1 = q - p + 1;
n2 = r - q;
if ((left = (int*)malloc((n1 + 1)*sizeof(int))) == NULL) {
perror("malloc error");
exit(1);
}
if ((right = (int*)malloc((n2 + 1)*sizeof(int))) == NULL) {
perror("malloc error");
exit(1);
}
for (i = 0; i < n1; i ++ ) {
left[i] = arr[p + i];
}
left[i] = MAX;
for (i = 0; i < n2; i ++ ) {
right[i] = arr[q + i + 1];
}
right[i] = MAX;
i = 0; j = 0;
for (k = p; (1); k ++ ) {
if (left[i] > right[j]) {
(2);
j ++ ;
} else {
arr[k] = left[i];
i ++ ;
}
}
}
void mergeSort(int arr[], int begin, int end) {
int mid;
if ((3)) {
mid = (begin + end) / 2;
mergeSort(arr, begin, mid);
(4);
merge(arr, begin, mid, end);
}
}
【问题1】(8分)
根据以上说明和C代码,填充(1)?(4)。
【问题2】(5分)
根据题干说明和以上C代码,算法采用了(5)算法设计策略。
分析时间复杂度时,列出其递归式为 (6) ,
解得渐进时间复杂度为(7)(用O符号表示)。空间复杂度为(8)(用O符号表示)。
【问题3】(2分)
两个长度分别为n1和n2的已经排好序的子数组进行归并,根据上述C代码,则元素之间比较次数为 (9) 2、快速排序
#include <stdio.h>
#include <stdlib.h>
int partition(int A[], int low, int high);
void Quicksort(int A[], int low, int high);
int main()
{
int A[] = { 32, 24, 89, 17, 4, 12 };
int n = sizeof(A) / sizeof(A[0]);
Quicksort(A, 0, n - 1);
for (int i = 0; i < n; i++)
{
printf("%d ", A[i]);
}
return 0;
}
int partition(int A[], int low, int high)
{
int pivot = A[low];
while (low < high)
{
while (low < high && A[high] >= pivot) high--;
A[low] = A[high];
while (low < high && A[low] <= pivot) low++;
A[high] = A[low];
}
A[low] = pivot;
return low;
}
void Quicksort(int A[], int low, int high)
{
if (low < high)
{
int pointpos = partition(A, low, high);
Quicksort(A, low, pointpos - 1);
Quicksort(A, pointpos + 1, high);
}
}3、分硬币(17上)
假币问题:有n枚硬币,其中有一枚是假币,已知假币的重量较轻。
现只有一个天平,要求用尽量少的比较次数找出这枚假币。
【分析问题】
将n枚硬币分成相等的两部分:
(1)当n为偶数时,将前后两部分,即1…n/2和n/2+1…n,放在天平的两端,
较轻的一端里有假币,继续在较轻的这部分硬币中用同样的方法找出假币;
(2)当n为奇数时,将前后两部分,即1…(n-1)/2和(n+1)/2+1…n,放在天平的两端,
较轻的一端里有假币,继续在较轻的这部分硬币中用同样的方法找出假币;
若两端重量相等,则中间的硬币,即第(n+1)/2枚硬币是假币。
【C代码】
coins[]:硬币数组
first, last:当前考虑的硬币数组中的第一个和最后一个下标。
#include <stdio.h>
int getCounterfeitCoin(int coins[], int first, int last) {
int firstSum = 0, lastSum = 0;
int i;
if (first == last - 1) { /* 只剩两枚硬币 */
if (coins[first] < coins[last])
return first;
return last;
}
if ((last - first + 1) % 2 == 0) { /* 偶数枚硬币 */
for (i = first; i < (1); i++) {
firstSum += coins[i];
}
for (i = first + (last - first) / 2 + 1; i < last + 1; i++) {
lastSum += coins[i];
}
if ((2)) {
return getCounterfeitCoin(coins, first,
first + (last - first) / 2);
}
else {
return getCounterfeitCoin(coins,
first + (last - first) / 2 + 1, last);
}
}
else { /*奇数枚硬币*/
for (i = first; i < first + (last - first) / 2; i++) {
firstSum += coins[i];
}
for (i = first + (last - first) / 2 + 1; i < last + 1; i++) {
lastSum += coins[i];
}
if (firstSum < lastSum) {
return getCounterfeitCoin(coins, first,
first + (last - first) / 2 - 1);
}
else if (firstSum > lastSum) {
return getCounterfeitCoin(coins,
first + (last - first) / 2 + 1, last);
}
else {
return (3);
}
}
}
【问题1】(6分)
根据题干说明,填充C代码中的空(1)?(3)。
【问题2】(6分)
根据题干说明和C代码,算法采用了(4)设计策略。
函数getCounterfeitCoin的时间复杂度为(5)(用O表示)。
【问题3】(3分)
若输入的硬币数为30,则最少的比较次数为(6),最多的比较次数为(7)。四、排序算法(???)
1、大根堆(22下)
1.堆排序思想

- 1.将无序序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆。
- 2.将堆顶元素与末尾元素交换,将最大元素”沉”到数组末端。
- 3.重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
?2.题目描述
排序是将一组无序的数据元素调整为非递减顺序的数据序列的过程,
堆排序是一种常用 的排序算法。用顺序存储结构存储堆中元素。
非递减堆排序的步骤是:
(1)将含 n 个元素的待排序数列构造成一个初始大顶堆,
存储在数组 R(R[1],R[2],..., R[n])中。此时堆的规模为 n,
堆顶元素 R[1]就是序列中最大的元素,R[n]是堆中最后一个 元素。
(2)将堆顶元素和堆中最后一个元素交换,最后一个元素脱离堆结构,
堆的规模减 1, 将堆中剩余的元素调整成大顶堆;
(3)重复步骤(2),直到只剩下最后一个元素在堆结构中,
此时数组 R 是一个非递减 的数据序列。
#define MAXITEM 100
/* 调正堆
* R:待排序数组;
* V:结点编号, 以 v 为根的二叉树, R[v] ≥ R[2v], R[v] ≥ R[2v + 1],
* 且其左子树和右子树都是大顶堆;
* n:堆结构的规模,即堆中的元素数
*/
void Heapify(int R[MAXITEM], int v, int n) {
int i, j;
i = v;
j = 2 * i;
R[0] = R[i];
while (j <= n) {
if (j < n && R[j] < R[j + 1]) {
j++;
}
if ((1)) {
R[i] = R[j];
i = j;
j = 2 * i;
}
else
{
j = n + 1;
}
}
R[i] = R[0];
}
/* 堆排序,R 为待排序数组:n 为数组大小 */
void HeapSort(int R[MAXITEM], int n) {
int i;
for (i = n / 2; i >= 1; i--) {
((2));
}
for (i = n;((3)); i--) {
R[0] = R[i];
R[i] = R[1];
((4));
Heapify(R, 1, i - 1);
}
}
【问题1】(8分)
根据题干说明,填充C代码中的空(1)?(4)。
【问题 2】(2 分)
根据以上说明和 C 代码,算法的时间复杂度为(5) (用 O 符号表示)。
【问题 3】(5 分)
考虑数据序列 R=(7,10,13,15,4,20,19,8),n=8,则构建的初始大顶堆为(6)
第一个元素脱离堆结构,对剩余元素再调整成大顶堆后的数组 R 为 (7) 2、希尔排序(20下)
1.算法思想

- 先将整个待排序的序列划分为若干个子序列,
- 然后分别对子序列排序,逐步缩小划分子序列的间隔,直到划分间隔为1时排序完成。
?2.题目描述
希尔排序算法又称最小增量排序算法,其基本思想是:
步骤1:构造一个步长序列delta1,?delta2,?....,?deltak,?其中delta1?=?n?/?2,后面的每个delta是前一个的1?/?2,deltak?=?1;
步骤2:根据步长序列进行k趟排序;
步骤3:对第i趟排序,根据对应的步长delta,将等步长位置元素分,对同一组内元素在原位置上进行直接插入排序。
【C代码】常量和变量
Data:待排序数组data,长度为n,待排序数据在data[0],?data[1],?data[2]...,?data[n?-?1]中。
N:数组data中的元素个数
delta:步长数组
#include <stdlib.h>
void ShellSort(int data[], int n) {
int* delta, k, i, t, dk, j;
k = n;
delta = (int*)malloc(sizeof(int) * (n / 2));
i = 0;
do {
(1);
delta[i++] = k;
} while (2);
i = 0;
while ((3)) {
for (k = delta[i]; k < n; ++k)
if (data[k] < data[k - dk]) {
t = data[k];
for (j = k - dk; j >= 0 && t < data[j]; j -= dk)
data[j + dk] = data[j];
(4);
}
++i;
}
}
【问题1】(8分)
根据说明和C代码,填充C代码中的空(1)?(4)。
【问题2】(4分)
根据说明和C代码,该算法的时间复杂度(5)(填写小于、等于或大于)。
该算法是否稳定 (6) (是或否)。
【问题3】(3分)
对数组(15, 9, 7, 8, 20, -1, 4)用希尔排序方法进行排序,
经过第一趟排后得到的数组为 (7) 。
五、简单动态规划(???)
1、01背包(19下)
给定i个物品的价值v[1…i]、小重量w[1…i]和背包容量T,每个物品装到背包里或者不装到背包里。求最优的装包方案,使得所得到的价值最大。
0-1背包问题具有最优子结构性质。定义c[i][T]为最优装包方案所获得的最大价值。
【C代码】常量和变量
T:背包容量
v[]:价值数组
w[]:重量数组
c[][]:c[i][j]表示前i个物品在背包容量为j的情况下最优装包方案所能获得的最大价值
#include <stdio.h>
#include <math.h>
#define N 6
#define maxT 1000
int c[N][maxT] = { 0 };
int Memoized_Knapsack(int v[N], int w[N], int T) {
int i;
int j;
for (i = 0; i < N; i++) {
for (j = 0; j <= T; j++) {
c[i][j] = -1;
}
}
return Calculate_Max_Value(v, w, N - 1, T);
}
int Calculate_Max_Value(int v[N], int w[N], int i, int j) {
int temp = 0;
if (c[i][j] != -1) {
return (1);
}
if (i == 0 || j == 0) {
c[i][j] == 0;
}
else {
c[i][j] = Calculate_Max_Value(v, w, i - 1, j);
if ((2)) {
temp = (3);
if (c[i][j] < temp) {
(4);
}
}
}
return c[i][j];
}
【问题1】(8分)
根据说明和C代码,填充C代码中的空(1)?(4)。
【问题2】(4分)
根据说明和C代码,算法采用了(5)设计策略。
在求解过程中,采用了(6)(自底向上或者自顶向下)的方式。
【问题3】(3分)
若5项物品的价值数组和重量数组分别为v[] = { 0, 1, 6, 18, 22, 28 }
和w[] = { 0, 1, 2, 5, 6, 7 }背包容量为T = 11,则获得的最大价值为(7)。2、最长递增子序列(14下)
计算一个整数数组a的最长递增子序列长度的方法描述如下:
假设数组a的长度为n,用数组b的元素b[i]记录以a[i]为结尾元素的最长递增子序列的长度,则数组a的最长递增子序列的长度表示如下,其中b[i]满足最优子结构,可递归定义为:
【C代码】常量和变量
a:长度为n的整数数组,待求其最长递增子序列
b:长度为n的数组,b[i]记录以a[i](0≤i<n)为结尾元素的最长递增子序列的长
度,其中0≤i<n
len:最长递增子序列的长度
i,j:循环变量
temp:临时变量
#include <stdio.h>
int maxL(int*b, int n) {
? int i, temp=0;
? for(i=0; i<n; i++) {
? ? if(b[i]>temp)
? ? ? temp=b[i];
? }
? return temp;
}
int main() {
? int n, a[100], b[100], i, j, len;
? scanf("%d", &n);
? for(i=0; i<n; i++) { ? ? ?
? ? scanf("%d", &a[i]);
? }
? ? ? (1) ? ?;
? for(i=1; i<n; i++) {
? ? for(j=0, len=0;?? ? (2) ? ?; j++) {
? ? ? if(?? ?(3) ? ??&& len<b[j])?
? ? ? ? len=b[j];
? ? }
? ??? ? (4) ? ?;
? }
? Printf("len:%d\n", maxL(b,n));
? printf("\n");
}
【问题1】(8分)
根据说明和C代码,填充C代码中的空(1)~(4)。
【问题2】(4分)??
根据说明和C代码,算法采用了?(5)?设计策略,时间复杂度为?(6)?(用O符号表示)。 ? ?
【问题3】(3分)
已知数组a={3,10,5,15,6,8},根据说明和C代码,给出数组b的元素值。3、最长公共子串(15下)
计算两个字符串和的最长公共子串(Longest Common Substring)。
假设字符串x和字符串y的长度分别为m和n,用数组c的元素c[i][j]记录x中前t个字符和y中前j个字符的最长公共子串的长度。c[i][j]满足最优子结构,其递归定义为:
计算所有c[i][j]的值,值最大的c[i][j]即为字符串x和y的最长公共子串的长度。根据该长度即和,确定一个最长公共子串。
【C代码】常量和变量
x, y:长度分别为m和n的字符串
c[i][j]:记录x中前i个字符和y中前j个字符的最长公共子串的长度
max:x和y的最长公共子串的长度
maxi, maxj:分别表示x和y的某个最长公共子串的最后一个字符在x和y中的位置(序号)
#include <stdio.h>
#include <string.h>
int c[50][50];
int maxi;
int maxj;
int lcs(char* x, int m, char* y, int n) {
int i, j;
int max = 0;
maxi = 0;
maxj = 0;
for (i = 0; i <= m; i++) c[i][0] = 0;
for (i = 1; i <= n; i++) c[0][i] = 0;
for (i = 1; i <= m; i++) {
for (j = 1; j <= n; j++) {
if ((1)) {
c[i][j] = c[i - 1][j - 1] + 1;
if (max < c[i][j]) {
(2);
maxi = i;
maxj = j;
}
}
else (3);
}
}
return max;
}
void printLCS(int max, char* x) {
int i = 0;
if (max == 0) return;
for ((4); i < maxi; i++)
printf("%c", x[i]);
}
void main() {
char* x = "ABCADAB";
char* y = "BDCABA";
int max = 0;
int m = strlen(x);
int n = strlen(y);
max = lcs(x, m, y, n);
printLCS(max, x);
}
【问题1】(8分)
根据以上说明和C代码,填充C代码中的空(1)?(4)。
【问题2】(4分)
根据题干说明和以上C代码,算法采用了 (5) 设计策略。
分析时间复杂度为 (6) (用O符号表示)。
【问题3】(3分)
根据题干说明和以上C代码,输入字符串x = "ABCADAB",
y = "BDCABA",则输出为 (7) 。六、复杂动态规划(???)
1、矩阵相乘(22上)
详细题解(一看就会):http://t.csdnimg.cn/XtVOS
某工程计算中要完成多个矩阵相乘(链乘)的计算任务,对矩阵相乘进行以下说明。
(1)两个矩阵相乘要求第一个矩阵的列数等于第二个矩阵的行数,计算量主要由进行乘法运算的次数决定。假设采用标准的矩阵相乘算法,计算,需要次乘法运算,即时间复杂度为
(2)矩阵相乘满足结合律,多个矩阵相乘时不同的计算顺序会产生不同的计算量。以矩阵三个矩阵相乘为例,若按计算,则需要进行次乘法运算,若按计算,则需要进行次乘法运算。
矩阵连乘问题可描述为:
给定个矩阵,对较大的,可能计算的顺序数量非常庞大,用蛮力法确定计算顺序是不实际的。经过对问题进行分析,发现矩阵连乘问题具有最优子结构,即若的一个最优计算顺序从第个矩阵处断开,即分为和两个子问题,则该最优解应该包含的一个最优计算顺序和的一个最优计算顺序。据此构造递归式:
#define N 100
int cost[N][N];
int trace[N][N];
int cmm(int n, int seq[]) {
int tempCost;
int tempTrace;
int i, j, k, p;
int temp;
for (i = 0; i < n; i++) { cost[i][i] = 0; }
for (p = 1; p < n; p++) {
for (i = 0; i < n - p; i++) {
(1);
tempCost = -1;
for (k = i; (2); k++) {
temp = (3);
if (tempCost == -1 || tempCost > temp) {
tempCost = temp;
tempTrace = k;
}
}
cost[i][j] = tempCost;
(4);
}
}
return cost[0][n - 1];
}
【问题1】(8分)
根据以上说明和C代码,填充C代码中的空(1)?(4)。
【问题2】(4分)
根据以上说明和C代码,该问题采用了 (5) 算法设计策略,
时间复杂度为 (6) 。(用O符号表示)
【问题3】(3分)
考虑实例n = 4,各个矩阵的维数:A1为15 * 5,A2为5 * 10,
A3为10 * 20,A4为20 * 25,即维数序列为15, 5, 10, 20, 25。
则根据上述C代码得到的一个最优计算顺序为(7)(用加括号方式表示计算顺序),
所需要的乘法运算次数为 (8) 。2、最短编辑距离(21下)
详细讲解(一看就会):407 线性DP 编辑距离_哔哩哔哩_bilibili
生物学上通常采用编辑距离来定义两个物种DNA序列的相似性,从而刻画物种之间的进化关系。具体来说,编辑距离是指将一个字符串变换为另一个字符所需要的最小操作次数。
操作有三种,分别为:
插入一个字符、删除一个字符以及将一个字符修改为另一个字符。
用字符数组str1和str2分别表示长度为len1和len2的字符串,
定义二维数组d记录求解编辑距离的子问题最优解,则该二维数组可以递归定义为:
【C代码】常量和变量
A,B:两个字符数组
d[][]:二维数组
i,j:循环变量
temp:临时变量
#include <stdio.h>
#define N 100
char A[N] = "CTGA";
char B[N] = "ACGCTA";
int d[N][N];
int min(int a, int b) {
return a < b ? a : b;
}
int editdistance(char* str1, int len1, char* str2, int len2) {
int i, j;
int diff;
int temp;
for (i = 0; i <= len1; i++) {
d[i][0] = i;
}
for (j = 0; j <= len2; j++) {
(1);
}
for (i = 1; i <= len1; i++) {
for (j = 1; j <= len2; j++) {
if ((2)) {
d[i][j] = d[i - 1][j - 1];
}
else {
temp = min(d[i - 1][j] + 1, d[i][j - 1] + 1);
d[i][j] = min(temp, (3));
}
}
}
return (4);
}
【问题1】(8分)
根据说明和C代码,填充C代码中的空(1)?(4)。
【问题2】(4分)
根据说明和C代码,算法采用了 (5) 设计策略,
时间复杂度为 (6) (用O符合表示,两个字符串的长度分别用m和n表示)。
【问题3】(3分)
已知两个字符串A = “CTGA”和B = “ACGCTA”,根据说明和C代码,
可得出这两个字符串的编辑距离为 (7) 。本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!