序列模型，语言模型，RNN的相关概念

序列模型，语言模型，RNN

循环神经网络（RNN）通过引入状态变量来存储过去的信息和当前的输入，从而确定当前的输出。这种结构使得RNN非常适合处理序列信息，因为它可以捕捉到序列中的时间依赖性。这与卷积神经网络（CNN）的工作方式形成了对比，CNN主要用于处理空间信息，如图像等。

序列模型概念

在序列模型中，预测

$$x_t～P(x_t|x_{t?1},...,x_1)$$

表示在给定前t-1个元素的条件下，第t个元素的概率分布。

自回归模型：这种模型假设当前的观测值只依赖于过去的一定数量（τ）的观测值。这样的好处是模型的参数数量始终是固定的，即使用观测序列$x_{t?1},...,x_{t?\tau }$，这使得我们可以训练一个深度网络。自回归模型的名字来源于它对自身的回归，即当前的观测值是过去观测值的函数。

隐变量自回归模型：这种模型除了考虑过去的观测值，还保留了一个对过去观测的总结（隐状态）。在这个模型中，我们不仅预测当前的观测值，而且还更新隐状态。这个模型被称为"隐变量自回归模型"，因为它包含了未被观测到的隐状态。在这个模型中，当前的观测值是基于隐状态的条件概率，隐状态则是基于过去的隐状态和过去的观测值的函数。

马尔可夫模型是一种统计模型，它假设系统在下一时刻的状态只依赖于它在当前时刻的状态，而与它在过去的所有状态都无关。这种性质被称为马尔可夫性质或马尔可夫条件。

例子：拟合正弦函数

在时间序列分析中，我们通常将序列数据转换为特征-标签对，以便于机器学习模型进行学习。这里的"嵌入维度" $\tau$ 是指我们用来预测当前数据点的历史数据点的数量。我们的特征 $x_t$ 是一个包含了前 $\tau$ 个数据点的向量，这个向量提供了预测 $y_t$ 所需要的上下文信息。

然而，对于序列的前 $\tau$ 个数据点，我们没有足够的历史记录来构建这样的特征向量。因此，如果我们有 $N$ 个数据点，我们只能构建 $N?\tau$ 个特征-标签对。这就是为什么我们的数据样本比原始序列少了 $\tau$ 个的原因。

例如，如果我们有一个时间序列 $[x_1,x_2,x_3,x_4,x_5]$ 并且我们选择嵌入维度 $\tau =2$，我们可以构建的特征-标签对包括：特征 $x_3=[x_1,x_2]$，标签 $y_3=x_3$；特征 $x_4=[x_2,x_3]$，标签 $y_4=x_4$；特征 $x_5=[x_3,x_4]$，标签 $y_5=x_5$。但我们不能为 $x_1$ 和 $x_2$ 构建特征，因为它们前面没有足够的数据点。

# 代码实现：
import torch
from torch import nn
from torch.utils.data import DataLoader, TensorDataset
import matplotlib.pyplot as plt

# 数据生成
T = 1000
time = torch.arange(1, T + 1, dtype=torch.float32)
x = torch.sin(0.01 * time) + torch.normal(0, 0.2, (T,))

# 数据预处理
tau = 4
features = torch.zeros((T - tau, tau))
for i in range(tau):
    features[:, i] = x[i:T - tau + i]
labels = x[tau:].reshape((-1, 1))

# 定义数据加载函数
def load_array(data_arrays, batch_size, is_train=True):
    dataset = TensorDataset(*data_arrays)
    return DataLoader(dataset, batch_size, shuffle=is_train)

# 加载数据
batch_size, n_train = 16, 600
train_iter = load_array((features[:n_train], labels[:n_train]), batch_size)

# 定义模型
def get_net():
    net = nn.Sequential(nn.Linear(4, 10), nn.ReLU(), nn.Linear(10, 1))
    net.apply(init_weights)
    return net

# 初始化网络权重的函数
def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.xavier_uniform_(m.weight)

# 定义损失函数
loss = nn.MSELoss(reduction='none')

# 定义训练函数
def train(net, train_iter, loss, epochs, lr):
    trainer = torch.optim.Adam(net.parameters(), lr)
    for epoch in range(epochs):
        for X, y in train_iter:
            trainer.zero_grad()
            l = loss(net(X), y)
            l.sum().backward()
            trainer.step()
        print(f'epoch {epoch + 1}, loss: {sum(loss(net(X), y)).item() / len(y):f}')

# 训练模型
net = get_net()
train(net, train_iter, loss, 5, 0.01)

# 预测
onestep_preds = net(features)
plt.plot(time, x, label='data')
plt.plot(time[tau:], onestep_preds.detach().numpy(), label='1-step preds')
plt.xlim([1, 1000])
plt.legend()
plt.show()

# k步预测
max_steps = 64
features = torch.zeros((T - tau - max_steps + 1, tau + max_steps))
for i in range(tau):
    features[:, i] = x[i:i + T - tau - max_steps + 1]
for i in range(tau, tau + max_steps):
    features[:, i] = net(features[:, i - tau:i]).reshape(-1)
steps = (1, 4, 16, 64)
for i in steps:
    plt.plot(time[tau + i - 1:T - max_steps + i], features[:, tau + i - 1].detach().numpy(), label=f'{i}-step preds')
plt.xlim([5, 1000])
plt.legend()
plt.show()

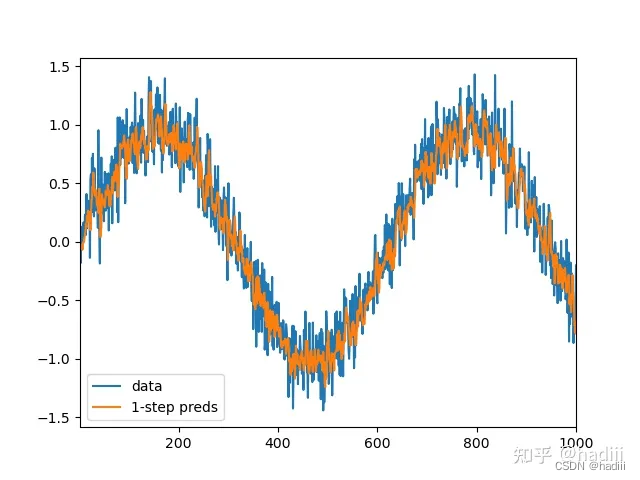
单步预测

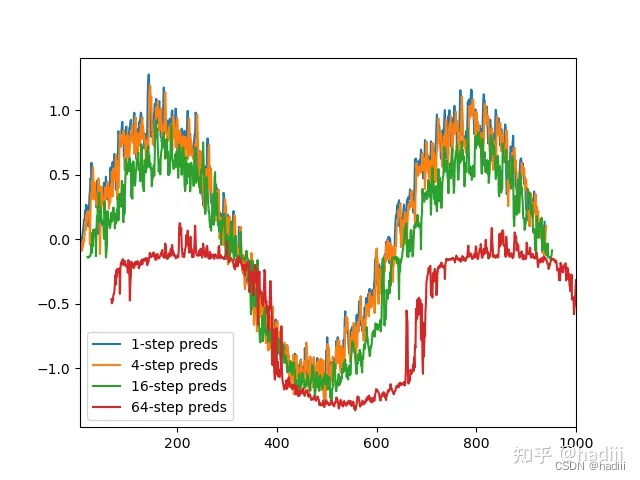
k步预测

对于直到时间步t的观测序列，其在时间步t + k的预测输出是“k步预测”。随着我们对预测时间k值的增加，会造成误差的快速累积和预测质量的极速下降。

语言模型概念

文本预处理：

1. 将文本作为字符串加载到内存中。
2. 将字符串拆分为词元（如单词和字符）。
3. 建立?个词表，将拆分的词元映射到数字索引（神经网络中用one-hot或者embedding）。
4. 将文本转换为数字索引序列，方便模型操作。

在自然语言处理中，我们经常需要对文档或词元序列进行建模。如果我们在单词级别对文本数据进行词元化，我们可以依赖于序列模型的分析。基本的概率规则如下：

$$P(x_1,x_2,...,x_T)=\prod _{t=1}^{T}P(x_t|x_1,...,x_{t?1})$$

例如，一个包含四个单词的文本序列的概率可以表示为：

$$P(\text{deep},\text{learning},\text{is},\text{fun})=P(\text{deep})P(\text{learning}|\text{deep})P(\text{is}|\text{deep},\text{learning})P(\text{fun}|\text{deep},\text{learning},\text{is})$$

为了训练语言模型，我们需要计算单词的概率，以及给定前几个单词后出现某个单词的条件概率。这些概率本质上就是语言模型的参数。

我们通常假设训练数据集是一个大型的文本语料库。训练数据集中词的概率可以根据给定词的相对词频来计算。例如，估计值 $\hat{P}(\text{deep})$ 可以计算为任何以单词“deep”开头的句子的概率。一种方法是统计单词“deep”在数据集中的出现次数，然后将其除以整个语料库中的单词总数。这种方法效果不错，特别是对于频繁出现的单词。然后，我们可以尝试估计：

$$\hat{P}(\text{learning}|\text{deep})=\frac{n(\text{deep},\text{learning})}{n(\text{deep})}$$

其中 $n(x)$ 和 $n(x,x^{\prime })$ 分别是单个单词和连续单词对的出现次数。不幸的是，由于连续单词对“deep learning”的出现频率要低得多，所以估计这类单词正确的概率要困难得多。特别是对于一些不常见的单词组合，要想找到足够的出现次数来获得准确的估计可能都不容易。

如果 $P(x_{t+1}|x_t,...,x_1)=P(x_{t+1}|x_t)$，则序列上的分布满足一阶马尔可夫性质。阶数越高，对应的依赖关系就越长。这种性质推导出了许多可以应用于序列建模的近似公式：

$$P(x_1,x_2,x_3,x_4)=P(x_1)P(x_2)P(x_3)P(x_4)$$

$$P(x_1,x_2,x_3,x_4)=P(x_1)P(x_2|x_1)P(x_3|x_2)P(x_4|x_3)$$

$$P(x_1,x_2,x_3,x_4)=P(x_1)P(x_2|x_1)P(x_3|x_1,x_2)P(x_4|x_2,x_3)$$

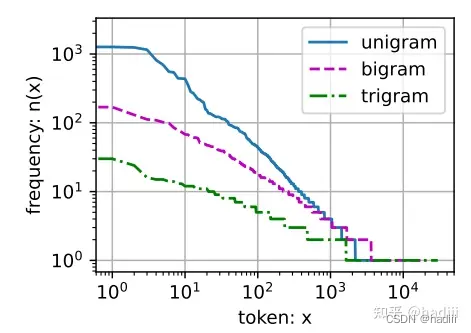
通常，涉及一个、两个和三个变量的概率公式分别被称为一元语法（unigram）、二元语法（bigram）和三元语法（trigram）模型。

齐普夫定律（Zipf’s law）：

语言中单词序列遵循齐普夫定律，同时很多n元组出现次数较少，说明语言中存在相当多的结构。

基于深度学习的模型在语言建模方面具有优势，因为它们能够处理稀疏数据并从中学习有用的特征和模式，而不像拉普拉斯平滑方法那样受限。

RNN概念

n元语法模型的局限性：在n元语法模型中，单词 $x_t$ 在时间步t的条件概率仅取决于前?n ? 1个单词。对于时间步t ? (n ? 1)之前的单词，如果我们想将其可能产?的影响合并到 $x_t$ 上，需要增加n，然而模型参数的数量也会随之呈指数增长，因为词表V需要存储 $|V{|}^3$ 个数字。

注意，RNN的参数是固定的。无论输入序列的长度如何，RNN的参数（包括输入到隐藏层的权重、隐藏层到隐藏层的权重、偏置项以及可能的隐藏层到输出层的权重等）都保持不变。有一些图示是按照时间步展开的，也就是进行了多次输入输出，横轴上的隐藏状态数并不是隐藏单元数。RNN在不同的时间步上使用的是相同的参数（权重和偏置）。

隐状态变量的长度（或者说维度）是由隐藏层的单元数决定的，而与输入序列的长度无关。每个隐藏单元都会有一个对应的隐状态值，因此隐状态变量的维度就等于隐藏层的单元数。这个隐状态变量会在每个时间步被更新，并用于计算下一个时间步的输出和新的隐状态。

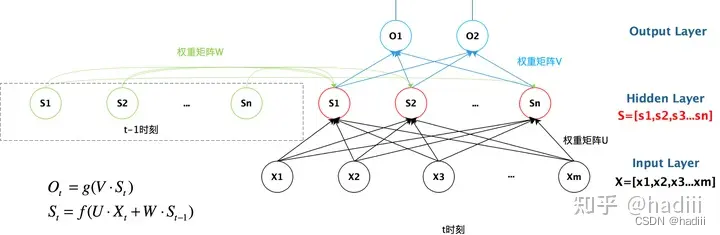
图源：忆臻

注意到，t-1时刻的隐变量是被保存下来的，它在网络中实体和t时刻的隐变量是同一个。

在n元语法模型中，单词 $x_t$ 在时间步 t 的条件概率仅取决于前面 n - 1 个单词。对于时间步 t - (n - 1) 之前的单词，如果我们想将其可能产生的影响合并到 $x_t$ 上，需要增加 n，然而模型参数的数量也会随之呈指数增长，因为词表 V 需要存储 $|V{|}^n$ 个数字。因此，与其将 $P(x_t|x_{t?1},...,x_{t?n+1})$ 建模，不如使用隐变量模型，它可以捕获序列中的长期依赖关系，而不仅仅是前 n - 1 个单词的信息。：

$$P(x_t|x_{t?1},...,x_{t?n+1})$$

其中 $h_{t?1}$ 是隐状态（hidden state），也称为隐藏变量（hidden variable），它存储了到时间步 t - 1 的序列信息。通常，我们可以基于当前输入 $x_t$ 和先前隐状态 $h_{t?1}$ 来计算时间步 t 处的任何时间的隐状态：

$$h_t=f(x_t,h_{t?1})$$

在下方提供的公式 中，新增了一项 $H_{t?1}?W_{hh}$，这一项表示前一个时间步的隐状态与一个权重矩阵 $W_{hh}$ 的乘积，这个乘积结果与当前时间步的输入一起决定了当前时间步的隐状态。这样的设计使得隐状态能够在时间步之间传递信息，实现了序列信息的记忆功能。

$$H_t=?(X_t{W}_{xh}+H_{t?1}{W}_{hh}+b_h)$$

$$O_t=H_t{W}_{hq}+b_q$$

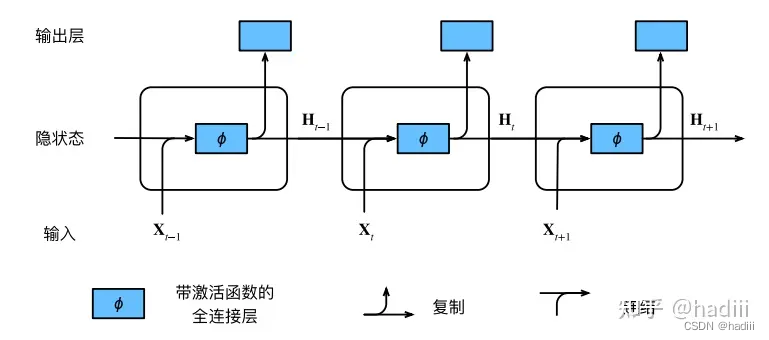
按时间步展开，具有隐状态的循环神经?络

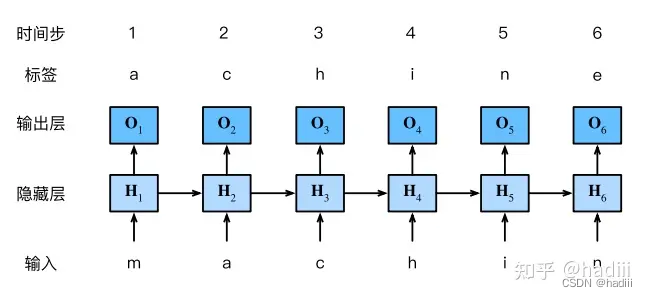
例子：字符级语言模型

交叉熵函数

交叉熵函数是用于衡量两个概率分布之间差异的度量，常用于分类任务中的损失函数。给定真实分布 $y$ 和模型预测分布 $\hat{y}$，交叉熵函数定义为：

$$l(y,\hat{y})=?\sum _{j=1}^q{y}_j\log {\hat{y}}_j$$

其中 $q$ 是类别的总数，$y_j$ 是真实分布的第 $j$ 项，${\hat{y}}_j$ 是模型预测分布的第 $j$ 项。

困惑度 (Perplexity)

困惑度是一个概率模型对给定测试数据集的预测能力的度量，直观上可以理解为模型在预测一个序列时的平均分支数或选择数。一个好的语言模型能够较准确地预测接下来可能出现的单词，因此具有较低的困惑度。困惑度的公式为：

$$\exp \left(?\frac{1}{n}\sum _{t=1}^n\log P(x_t|x_{t?1},\dots ,x_1)\right)$$

其中 $P(x_t|x_{t?1},\dots ,x_1)$ 是在给定前面单词的条件下，模型预测当前单词 $x_t$ 的概率。

梯度剪裁 (Gradient Clipping)

对于长度为 $T$ 的序列，我们在迭代中计算这 $T$ 个时间步上的梯度，将会在反向传播过程中产生长度为 $O(T)$ 的矩阵乘法链。梯度剪裁通过限制梯度的大小来解决梯度爆炸问题，确保梯度在一个合理的范围内，从而避免梯度过大导致的问题。梯度剪裁的公式为：

$$g\leftarrow \min \left(1,\frac{\theta }{\Vert g\Vert }\right)g$$

其中 $g$ 是梯度向量，$\theta$ 是梯度剪裁的阈值，$\Vert g\Vert$ 是梯度向量的范数。