一种可扩展的多属性可控文本生成即插即用方法
《An extensible plug-and-play method for multi-aspect controllable text generation》论文解读
文章的主要工作
(1)提出了一种可扩展的即插即用方法,PROMPT GATING,用于多方面可控文本生成,它能够通过简单地连接插件来控制训练时未见的方面组合。
(2)为相互干扰问题提供了理论下界和实证分析,我这将有助于未来的研究。
(3)实验表明,我们的方法相互干扰较低,在文本质量、约束准确性和可扩展性方面优于强基线。
总体架构

图1:概述我们提出的用于多方面可控文本生成的可扩展即插即用方法。首先,插件分别在单方面标记数据上进行训练(左)。然后,可以通过简单的串联来组合任意插件,并将其插入到预训练模型中以满足相应的约束组合(右)。由于不同插件的单独训练,扩展新约束的成本相对较低。此外,我们的方法抑制了相互干扰的积累,减轻了约束的退化。
背景
一般来说,前缀调整将轻量级连续向量前置到每个 Transformer 层的多头注意力子层:
H
=
Att
(
Q
,
[
P
K
;
K
]
,
[
P
V
;
V
]
)
(1)
H = \text{Att}(Q, [P^K; K], [P^V; V])\tag{1}
H=Att(Q,[PK;K],[PV;V])(1)
Att
(
?
)
\text{Att}(·)
Att(?) 是注意力函数,
Q
Q
Q 是输入查询,
K
K
K 和
V
V
V 是输入的激活值,
P
K
P^K
PK 和
P
V
P^V
PV 是可训练的前缀,
[
;
]
[;]
[;] 表示串联操作,
H
H
H 是注意力子层的输出。我们使用
?
\phi
? 来表示所有 Transformer 层中的前缀集合。
具体而言,对于多方面可控文本生成,我们假设存在 N N N 个方面的约束。
?
^
i
=
arg
?
max
?
?
i
{
P
(
y
∣
x
;
θ
,
?
i
)
}
,
1
≤
i
≤
N
(2)
\hat{\phi}_i = \underset{\phi_i}{\arg\max} \{ P(y|x; \theta, \phi_i) \}, 1 \leq i \leq N\tag{2}
?^?i?=?i?argmax?{P(y∣x;θ,?i?)},1≤i≤N(2)
其中
θ
\theta
θ是预训练模型的固定参数,
y
y
y是受控的目标句子,
x
x
x是输入句子,
P
(
y
∣
x
;
θ
,
?
i
)
P(y|x; \theta, \phi_i)
P(y∣x;θ,?i?)是在给定
x
x
x的条件下
y
y
y的概率,
?
^
i
\hat{\phi}_i
?^?i?是第
i
i
i个方面的前缀的学习参数。
在推理过程中,对于多个方面的组合,相应的前缀被选择并通过连接(Qian et al., 2022; Yang et al., 2022)或找到它们的交集(Gu et al., 2022)来合成,然后生成过程基于这种合成进行。在不失一般性的情况下,我们以两个方面为例。条件概率可以表示为
P ( y ^ ∣ x ; θ , syn ( ? ^ 1 , ? ^ 2 ) ) , ( 3 ) P(\hat{y}|x; \theta, \text{syn}(\hat{\phi}_1, \hat{\phi}_2)),\quad (3) P(y^?∣x;θ,syn(?^?1?,?^?2?)),(3)
其中, syn ( ? ) \text{syn}(\cdot) syn(?) 是一个合成函数, y ^ \hat{y} y^? 是候选句子, ? ^ 1 \hat{\phi}_1 ?^?1? 和 ? ^ 2 \hat{\phi}_2 ?^?2? 是两组对应于两个方面(例如,对于情感是“positive”,对于话题是“sports”)的前缀。
相互干扰的分析
定义
“相互干扰(MI)”是指在推理阶段(即零样本设置)时,多个单独训练但同时指导预训练模型的插件之间的干扰。然而,由于深度神经网络的复杂性,确切的干扰分析是困难的。直观上,如果在训练期间多个插件是同时优化的,这需要多方面标记的数据,它们的干扰将被最小化,因为它们已经学会在监督下合作地工作(即在监督设置中)。因此,我们使用在监督和零样本设置下隐藏状态的差异来近似估计多个插件的相互干扰。具体来说,让
?
^
i
\hat{\phi}_i
?^?i? 和
?
~
i
\tilde{\phi}_i
?~?i? 分别是从单方面和多方面标记数据中学习的插件的参数。以双方面控制为例,Transformer层的输出由
H
(
x
,
?
^
1
,
?
^
2
)
H(x, \hat{\phi}_1, \hat{\phi}_2)
H(x,?^?1?,?^?2?)给出,其中 x 是层输入,那么相互干扰可以定义为:
M
I
≈
∥
H
(
x
,
?
^
1
,
?
^
2
)
?
H
(
x
,
?
~
1
,
?
~
2
)
∥
.
(4)
MI \approx \left\| H(x, \hat{\phi}_1, \hat{\phi}_2) - H(x, \tilde{\phi}_1, \tilde{\phi}_2) \right\|.\tag{4}
MI≈
?H(x,?^?1?,?^?2?)?H(x,?~?1?,?~?2?)
?.(4)
实证分析
由于互相干扰已被定义为零样本和有监督设置中隐藏状态间差距的范数,我们可以在真实数据集上对其进行实证估计。通过计算Yelp数据集(Lample et al., 2019)上的平均范数,我们在图2中绘制了Prompt-tuning(Lester et al., 2021)和Prefix-tuning(Li and Liang, 2021)中互相干扰随Transformer层数变化的趋势。我们发现,随着可训练参数的插入,干扰逐渐累积。此外,最后一个Transformer层(即图2中的第12层)的互相干扰幅度与性能差距一致,性能差距是单一方面和多方面设置中约束满足度之间的差异(见表1)。同时,过少的可训练参数无法有效指导预训练模型。总结来说,为了在零样本设置中保持有效,关键是在提供足够的可训练参数以提高有监督性能的同时,限制互相干扰的增长(以降低性能差距)。
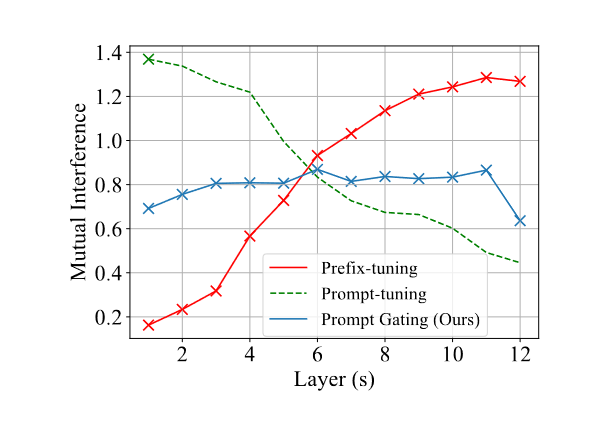
图2:互干扰随Transformer层数的变化。注意,“×”表示连续向量的插入。 Prompt-tuning 仅在嵌入层之后将向量插入到模型中,而其他两种方法将向量插入到每个 Transformer 层中。我们的方法(Prompt Gating)抑制相互干扰的增长,同时插入足够的可训练参数。
理论分析
为了找到减轻相互干扰的方法,我们进行了理论分析。
由于前馈和 Layernorm 子层是位置操作,不会引入插件的干扰,因此我们重点分析多头注意力(MHA)子层。
根据之前的研究,具有前缀的单个注意力头的输出,即第i个插件的输出,可以表示为:
h i = λ ( x i ) h ˉ i + ( 1 ? λ ( x i ) ) Δ h i = s i h ˉ i + t i Δ h i , ( 8 ) h_i = \lambda(x_i)\bar{h}_i + (1 - \lambda(x_i))\Delta h_i \\ = s_i\bar{h}_i + t_i\Delta h_i, \quad (8) hi?=λ(xi?)hˉi?+(1?λ(xi?))Δhi?=si?hˉi?+ti?Δhi?,(8)
其中, h ˉ i \bar{h}_i hˉi? 表示预训练的生成模型以 x i x_i xi?作为输入的原始输出。 λ ( x i ) \lambda(x_i) λ(xi?) 是与注意力权重相关的标量,其中 λ ( x i ) = s i \lambda(x_i) = s_i λ(xi?)=si?, 1 ? λ ( x i ) = t i 1 - \lambda(x_i) = t_i 1?λ(xi?)=ti?, t i ∈ ( 0 , 1 ) t_i \in (0, 1) ti?∈(0,1)。此外, Δ h i \Delta h_i Δhi? 是由第i个插件确定的偏移量,其大小与参数集 ? i \phi_i ?i?的大小成正比,其中 ? i \phi_i ?i?是第i个插件的参数集。
依据上述模式,当同时插入第i个和第j个插件时,头部的输出(即 h i , j h_{i,j} hi,j? )变为:
h i , j = γ h ^ i , j + α Δ h i + β Δ h j , ( 9 ) h_{i,j} = \gamma \hat{h}_{i,j} + \alpha \Delta h_i + \beta \Delta h_j, \quad (9) hi,j?=γh^i,j?+αΔhi?+βΔhj?,(9)
其中, h ^ i , j \hat{h}_{i,j} h^i,j? 是预训练的生成模型的输出,而 α \alpha α, β \beta β, γ \gamma γ 均属于 ( 0 , 1 ) (0, 1) (0,1) 区间,且满足 α < t i \alpha < t_i α<ti?, β < t j \beta < t_j β<tj?, γ < s i \gamma < s_i γ<si?, γ < s j \gamma < s_j γ<sj?。类似地, Δ h i \Delta h_i Δhi? 和 Δ h j \Delta h_j Δhj? 分别由第i个和第j个插件确定。
根据方程(4)中的定义,让 h ^ i , j \hat{h}_{i,j} h^i,j? 和 h ~ i , j \tilde{h}_{i,j} h~i,j? 分别为在多方面和单方面标签数据训练后的输出,类似于 h i , j h_{i,j} hi,j?。单个头部中两个插件的相互干扰(即, M I s MI_s MIs?)可以通过监督和零次推断下输出间差距的范数来衡量:
M I s = ∥ h ^ i , j ? h ~ i , j ∥ = ∥ h ^ i , j ? ( γ h ^ i , j + α Δ h i + β Δ h j ) ∥ ≥ ∥ h ^ i , j ? γ h ^ i , j ∥ ? ∥ α Δ h i + β Δ h j ∥ , ( 10 ) MI_s = \| \hat{h}_{i,j} - \tilde{h}_{i,j} \| \\ = \| \hat{h}_{i,j} - (\gamma \hat{h}_{i,j} + \alpha \Delta h_i + \beta \Delta h_j) \| \\ \geq \| \hat{h}_{i,j} - \gamma \hat{h}_{i,j} \| - \| \alpha \Delta h_i + \beta \Delta h_j \|, \quad (10) MIs?=∥h^i,j??h~i,j?∥=∥h^i,j??(γh^i,j?+αΔhi?+βΔhj?)∥≥∥h^i,j??γh^i,j?∥?∥αΔhi?+βΔhj?∥,(10)
其中, Δ h ^ i \Delta \hat{h}_i Δh^i? 和 Δ h ^ j \Delta \hat{h}_j Δh^j? 对应于插件在单方面标签数据训练时的偏移量。
考虑到由两个插件同时引起的干预应大于两个单独干预的总和,因为两个插件之间的相互作用,我们假设:
∥ h ^ i , j ? h ~ i , j ∥ > ∥ h ^ i ? h ~ i ∥ + ∥ h ^ j ? h ~ j ∥ . ( 11 ) \| \hat{h}_{i,j} - \tilde{h}_{i,j} \| > \| \hat{h}_i - \tilde{h}_i \| + \| \hat{h}_j - \tilde{h}_j \|. \quad (11) ∥h^i,j??h~i,j?∥>∥h^i??h~i?∥+∥h^j??h~j?∥.(11)
基于此,我们可以推导出:
M I s > ∥ h ^ i ? γ h ^ i ∥ + ∥ h ^ j ? γ h ^ j ∥ ? ∥ α Δ h ^ i + β Δ h ^ j ∥ . ( 12 ) MI_s > \| \hat{h}_i - \gamma \hat{h}_i \| + \| \hat{h}_j - \gamma \hat{h}_j \| - \| \alpha \Delta \hat{h}_i + \beta \Delta \hat{h}_j \|. \quad (12) MIs?>∥h^i??γh^i?∥+∥h^j??γh^j?∥?∥αΔh^i?+βΔh^j?∥.(12)
鉴于 s i > γ s_i > \gamma si?>γ, s j > γ s_j > \gamma sj?>γ, 并且 h ^ i = s i h ^ i + t i Δ h ^ i \hat{h}_{i} = s_i\hat{h}_i + t_i\Delta \hat{h}_i h^i?=si?h^i?+ti?Δh^i? (方程(8)), M I s MI_s MIs? 满足:
M I s > ∥ h ^ i ? s i h ^ i ∥ + ∥ h ^ j ? s j h ^ j ∥ ? ∥ α Δ h ^ i + β Δ h ^ j ∥ = ∥ t i Δ h ^ i ∥ + ∥ t j Δ h ^ j ∥ ? ∥ α Δ h ^ i + β Δ h ^ j ∥ ≥ ( t i ? α ) ∥ Δ h ^ i ∥ + ( t j ? β ) ∥ Δ h ^ j ∥ , ( 13 ) MI_s > \| \hat{h}_i - s_i\hat{h}_i \| + \| \hat{h}_j - s_j\hat{h}_j \| - \| \alpha \Delta \hat{h}_i + \beta \Delta \hat{h}_j \| \\ = \| t_i\Delta \hat{h}_i \| + \| t_j\Delta \hat{h}_j \| - \| \alpha \Delta \hat{h}_i + \beta \Delta \hat{h}_j \| \\ \geq (t_i - \alpha) \| \Delta \hat{h}_i \| + (t_j - \beta) \| \Delta \hat{h}_j \|, \quad (13) MIs?>∥h^i??si?h^i?∥+∥h^j??sj?h^j?∥?∥αΔh^i?+βΔh^j?∥=∥ti?Δh^i?∥+∥tj?Δh^j?∥?∥αΔh^i?+βΔh^j?∥≥(ti??α)∥Δh^i?∥+(tj??β)∥Δh^j?∥,(13)
其中 1 > t i ? α > 0 1 > t_i - \alpha > 0 1>ti??α>0 和 1 > t j ? β > 0 1 > t_j - \beta > 0 1>tj??β>0。因此,单个头部中两个插件的相互干扰有一个正的下界,并且与 ? i \phi_i ?i? 和 ? j \phi_j ?j? 的大小成正相关。
进一步,我们在多头场景中推导了MI的下界。假设 K K K 表示头部的数量, W W W 表示MHA中固定的输出投影矩阵, W o = Q o R o W_o = Q_oR_o Wo?=Qo?Ro? 是 W o W_o Wo? 的QR分解格式, λ o \lambda_o λo? 是平均绝对特征值。具体来说, h ^ i , j k \hat{h}^k_{i,j} h^i,jk? 和 h ~ i , j k \tilde{h}^k_{i,j} h~i,jk? 分别表示在第k个头部的 h ^ i , j \hat{h}_{i,j} h^i,j? 和 h ~ i , j \tilde{h}_{i,j} h~i,j?。然后,MHA中MI的下界(即, M I m MI_m MIm?)可以推导为(简单地将 R o R_o Ro? 视为对角矩阵):
M I m = ∥ c o n c a t ( h ^ i , j k ? h ~ i , j k ) K W o ∥ = ∥ c o n c a t ( h ^ i , j k ? h ~ i , j k ) K Q o R o ∥ ≈ λ o ∥ c o n c a t ( h ^ i , j k ? h ~ i , j k ) K Q o ∥ = λ o ∑ k = 1 K ∥ h ^ i , j k ? h ~ i , j k ∥ 2 ≥ λ o n ∑ k = 1 K ( ( t i k ? α k ) ∥ Δ h ^ i k ∥ + ( t j k ? β k ) ∥ Δ h ^ j k ∥ ) , ( 14 ) MI_m = \| concat(\hat{h}^k_{i,j} - \tilde{h}^k_{i,j})^K W_o \| \\ = \| concat(\hat{h}^k_{i,j} - \tilde{h}^k_{i,j})^K Q_oR_o \| \\ \approx \lambda_o \| concat(\hat{h}^k_{i,j} - \tilde{h}^k_{i,j})^K Q_o \| \\ = \lambda_o \sqrt{\sum_{k=1}^K \| \hat{h}^k_{i,j} - \tilde{h}^k_{i,j} \|^2} \\ \geq \frac{\lambda_o}{\sqrt{n}} \sum_{k=1}^K \left( (t^k_i - \alpha^k) \| \Delta \hat{h}^k_i \| + (t^k_j - \beta^k) \| \Delta \hat{h}^k_j \| \right), \quad (14) MIm?=∥concat(h^i,jk??h~i,jk?)KWo?∥=∥concat(h^i,jk??h~i,jk?)KQo?Ro?∥≈λo?∥concat(h^i,jk??h~i,jk?)KQo?∥=λo?k=1∑K?∥h^i,jk??h~i,jk?∥2?≥n?λo??k=1∑K?((tik??αk)∥Δh^ik?∥+(tjk??βk)∥Δh^jk?∥),(14)
其中 1 > t i k ? α k > 0 1 > t^k_i - \alpha^k > 0 1>tik??αk>0 和 1 > t j k ? β k > 0 1 > t^k_j - \beta^k > 0 1>tjk??βk>0,
Δ h ^ i k \Delta \hat{h}^k_i Δh^ik? 和 Δ h ^ j k \Delta \hat{h}^k_j Δh^jk? 也与 ? i \phi_i ?i? 和 ? j \phi_j ?j? 的大小正相关。
因此,多个插件之间的相互干扰具有理论上的正向下限,这意味着将分别训练的前缀串联起来与受监督训练的前缀相比存在不可修复的差距。结果,像图2中所示,相互干扰可能会随着模型深度的增加而累积。直观地说,引入含有可训练系数(这些系数在0到1之间)的门控到 ? ^ i \hat{\phi}_i ?^?i?中,对于减少方程(14)中的偏差以及因此产生的相互干扰是有帮助的。
结果发现,由于注意力子层之间的相互作用而引起的相互干扰有一个理论上的下界:
M
I
>
α
∥
Δ
h
1
(
x
,
?
^
1
)
∥
+
β
∥
Δ
h
2
(
x
,
?
^
2
)
∥
,
(
5
)
MI > \alpha \lVert \Delta h_1(x, \hat{\phi}_1) \rVert + \beta \lVert \Delta h_2(x, \hat{\phi}_2) \rVert, \quad (5)
MI>α∥Δh1?(x,?^?1?)∥+β∥Δh2?(x,?^?2?)∥,(5)
其中
0
<
α
,
β
<
1
0 < \alpha, \beta < 1
0<α,β<1,并且
∥
Δ
h
i
(
x
,
?
^
i
)
∥
\lVert \Delta h_i(x, \hat{\phi}_i) \rVert
∥Δhi?(x,?^?i?)∥ 是一个与
?
^
i
\hat{\phi}_i
?^?i? 的幅度正相关的范数。此外,下界可能会随着Transformer层的增加(如图2中所示)而增加。直观上来说,应用规范化(例如,门控)到第i个插件的参数以减少其幅度,将会减少互相干扰的下界。
PROMPT GATING
总体架构
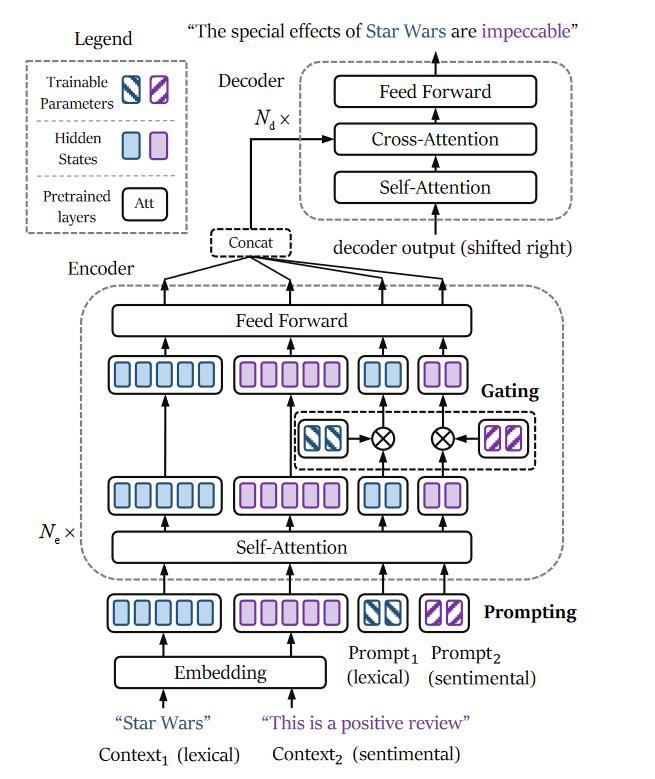
图 3:我们方法的架构。它展示了双向控制文本生成的推理阶段的情况。蓝色和紫色分别代表词汇和情感约束。连续的提示和上下文被输入到模型中,并应用可训练的门来引导预训练的模型并减轻插件的相互干扰。
尽管前缀调整(prefix-tuning)通过在每个注意力子层中插入连续向量,提供了足够的干预并避免了长范围依赖性,但它却受到这些插件相互干扰累积的影响。一方面,这些向量被插入到注意力子层中,在那里它们相互作用,这直接增强了它们之间的相互干扰。另一方面,这些向量没有被标准化,这导致了相互干扰的较大下界(参见方程式(5))。直观上,以逐位置(position-wise)的方式注入这些向量将避免它们之间的直接交互。此外,对这些向量进行标准化可以限制下界的幅度,这可能会减少相互干扰。因此,我们首先提出在注意力子层之外附加向量,这可以通过在嵌入层的输出上追加可训练的向量,并在每个Transformer层中的隐藏状态上添加可训练向量来实现(见图3)。然后,应用可训练的门控机制(trainable gates)到这些隐藏状态上,以进一步减轻相互干扰。通过这种方式,我们希望我们的方法能在提供足够的干预的同时,限制相互干扰的增长。
方法
Prompting
我们按照前向传播的顺序展示我们的模型。为了改变可训练参数注入模型的方式,我们首先遵循提示调整(Lester et al., 2021),将可训练提示附加到嵌入层的输出。此外,为了使我们的模型不仅适用于分类方面(例如,情感),而且适用于自由形式方面(例如,词汇约束),我们以文本形式呈现方面的约束并将其输入模型。当推理过程中需要两个方面的约束时,模型输入由下式给出
H
(
0
)
=
[
E
(
x
)
;
E
(
c
1
)
;
E
(
c
2
)
;
P
1
(
0
)
;
P
2
(
0
)
]
,
(
6
)
H^{(0)} = \left[ E(x); E(c_1); E(c_2); P_1^{(0)}; P_2^{(0)} \right], \quad (6)
H(0)=[E(x);E(c1?);E(c2?);P1(0)?;P2(0)?],(6)
在文中直接使用的翻译和LaTeX公式如下:
其中 E ( ? ) E(\cdot) E(?) 是嵌入函数,而 x x x 是用于序列到序列生成,如机器翻译的源句子,可以被省略。 c 1 c_1 c1? 和 c 2 c_2 c2? 是文本生成的约束条件(例如,“This is a positive review”用于生成积极评论,而“New York”用于词汇约束)。 P 1 ( 0 ) , P 2 ( 0 ) P_1^{(0)}, P_2^{(0)} P1(0)?,P2(0)? 是属于 R p × d \mathbb{R}^{p \times d} Rp×d 的连续提示,其中右上角的 ( j ) (j) (j) 表示第 j j j 层, p p p 是连续向量的数量, d d d 是隐藏状态的维度。为了避免训练和推理中位置上的差异,每个文本序列有自己从1开始的位置索引和它自己的段落嵌入(Devlin et al., 2019)。注意,在训练期间,只有一个文本约束和一组可训练参数被注入。
Gating
门控机制。模型输入 H ( 0 ) H^{(0)} H(0) 被送入编码器,其中可训练的门以逐位置的方式附加到隐藏状态上,这不仅减轻了相互干扰,也引导了模型的方向。具体来说, A ^ ( j ) = Self-Att ( H ( j ? 1 ) ) \hat{A}^{(j)} = \text{Self-Att}(H^{(j-1)}) A^(j)=Self-Att(H(j?1)) 是第 j j j 个注意力子层的输出,并且通过门进行了标准化:
A ^ ( j ) = [ A X ( j ) ; σ ( G 1 ( j ) ) ⊙ ( A 1 ( j ) + P 1 ( j ) ) ; σ ( G 2 ( j ) ) ⊙ ( A 2 ( j ) + P 2 ( j ) ) ] , ( 7 ) \hat{A}^{(j)} = \left[ \begin{array}{c} A_X^{(j)} ; \sigma(G_1^{(j)}) \odot (A_1^{(j)} + P_1^{(j)}); \sigma(G_2^{(j)}) \odot (A_2^{(j)} + P_2^{(j)}) \end{array} \right], \quad (7) A^(j)=[AX(j)?;σ(G1(j)?)⊙(A1(j)?+P1(j)?);σ(G2(j)?)⊙(A2(j)?+P2(j)?)?],(7)
其中, A X ( j ) ∈ R ( ∣ x ∣ + ∣ c 1 ∣ + ∣ c 2 ∣ ) × d A_X^{(j)} \in \mathbb{R}^{(|x|+|c_1|+|c_2|) \times d} AX(j)?∈R(∣x∣+∣c1?∣+∣c2?∣)×d 和 A i ( j ) ∈ R p × d A_i^{(j)} \in \mathbb{R}^{p \times d} Ai(j)?∈Rp×d 是从 A ^ ( j ) \hat{A}^{(j)} A^(j) 分离出的隐藏状态, P i ( j ) ∈ R p × d P_i^{(j)} \in \mathbb{R}^{p \times d} Pi(j)?∈Rp×d 是添加到隐藏状态中的可训练向量, σ \sigma σ 是 sigmoid 函数, G i ( j ) ∈ R p × d G_i^{(j)} \in \mathbb{R}^{p \times d} Gi(j)?∈Rp×d 是可训练向量。 ⊙ \odot ⊙ 表示哈达玛积(Hadamard product),标准化的向量 σ ( G i ( j ) ) \sigma(G_i^{(j)}) σ(Gi(j)?) 作为门来选择性地重新缩放注意力子层的输出,并以逐位置的方式进行。 A ^ ( j ) ∈ R ( ∣ x ∣ + ∣ c 1 ∣ + ∣ c 2 ∣ + 2 p ) × d \hat{A}^{(j)} \in \mathbb{R}^{(|x|+|c_1|+|c_2|+2p) \times d} A^(j)∈R(∣x∣+∣c1?∣+∣c2?∣+2p)×d 是标准化的结果。接下来,标准化的输出被送入前向子层: H ( j ) = FFN ( A ^ ( j ) ) H^{(j)} = \text{FFN}(\hat{A}^{(j)}) H(j)=FFN(A^(j))。最后,最后一个编码器层的输出被送入标准的 Transformer 解码器以引导文本生成。
训练与推理
如图1所示,在训练过程中,每个插件(包括提示和门)针对单一约束方面与预训练生成模型相结合,并通过相应的单一方面标记数据独立优化(参见方程(2))。相反,在推理过程中,可以通过简单地连接相应的插件来实现任意组合方面的控制(参见方程(3))。
此外,我们的方法对于已存在和新引入的约束的训练和推理过程进行了相同的处理。 N N N 个已存在方面和 M M M 个新添加方面的总训练成本是 O ( ( N + M ) C ) O((N + M)C) O((N+M)C),其中 C C C 表示单一方面上的训练成本。通过这种方式,引入新约束的成本相对较低。
实验
多属性受控文本生成
数据集
继之前的工作(Yang 等人,2022)之后,我们采用了广泛使用的 Yelp 数据集(Lample 等人,2019),其中包含带有情绪(正面和负面)和主题(美国、墨西哥和墨西哥)的餐厅评论。亚洲)标签。为了评估方法的可扩展性,我们添加了两个额外的约束方面:关键字(He,2021)和时态(过去和现在)(Ficler 和 Goldberg,2017),其中它们的标签是从评论中自动提取的。
评估
继之前的工作之后,我们采用自动和人工评估约束准确性和文本质量(Lyu et al., 2021;Dathathri et al., 2019;Gu et al., 2022)。具体来说,我们微调了两个基于 RoBERTa(Liu et al., 2019)的分类器来评估情绪和主题。时态准确性通过训练集中采用的相同工具进行评估,我们使用单词级复制成功率(CSR)(Chen et al., 2020)来评估词汇约束。此外,我们使用 GPT-2medium (Radford et al., 2019) 给出的困惑度 (PPL) 和平均清晰度 (Li et al., 2016) 分别评估生成文本的流畅性和多样性。对于人工评估,每个句子在情感、主题相关性以及流畅性方面均获得 1 至 5 分的评分,由三位评估者给出。最终分数是三个评分的平均分。
BaseLine
我们将我们的方法与多方面可控文本生成的几种代表性方法进行了比较:
- GEDI(Krause等人,2021年):这是一种在解码时期使用轻量级条件生成判别器来引导预训练模型的调节方法。通过多个判别器给出的分布经过归一化处理,以控制目标句子的多个方面。
- DIST. LENS(Gu等人,2022年):这是一种基于前缀调整的方法,它引入了自动编码器和额外的目标来将多个属性的约束映射到一个潜在空间(即前缀的联合训练)。在推理过程中,它找到多个约束的前缀的交集。
- PROMPT-TUNING(Lester等人,2021年):这是一种参数高效的方法,它在模型输入时附加连续的提示。多个提示分别进行训练,并在推理过程中简单地连接起来。
- PREFIX-TUNING(Li和Liang,2021年):这是一种参数高效的方法,它在注意力子层的激活上附加连续的前缀。多个前缀分别进行训练,并在推理过程中简单地连接起来。
- TAILOR(Yang等人,2022年):这是一种基于提示调整的方法,在推理过程中进一步修改注意力掩码和位置索引,以缩小训练和推理之间的差距。
结果
表1展示了双重方面可控文本生成的自动评估结果。我们展示了平均准确率以代表在满足多个约束方面的整体性能。此外,我们提供了双重方面和单一方面设置之间的性能差距,以表示以零样本方式结合多个插件的能力。尽管GEDI在情感准确率和独特性上获得了最高分,但其困惑度激增,且时态准确率显著下降,这可以归因于多个判别器的插值作用。由于PROMPT-TUNING没有足够的可训练参数,因此在约束准确率上表现不佳。然而,由于只插入一次向量,它的性能差距相对较小。PREFIX-TUNING由于在所有Transformer层中插入,受到严重的相互干扰,导致在约束准确率或困惑度上表现不佳。与PREFIX-TUNING相比,DIST. LENS由于前缀的联合训练,具有更好的约束准确性和较低的性能差距。我们发现DIST. LENS对训练集中的约束分布敏感,因为它试图找到多个约束的交集。我们的方法(PROMPT GATING)在插件分别训练的同时,实现了最高的约束准确率、最低的困惑度和相对较小的性能差距。
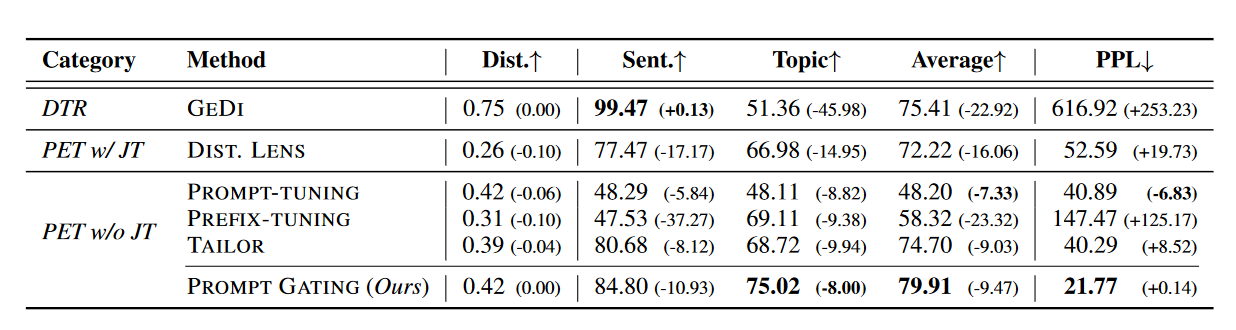
表1:双面可控文本生成的自动评估。 “DTR”和“PET”分别表示解码时间调节和参数有效调整方法。 “w/ JT”和“w/o JT”分别表示有和没有联合训练的方法。有两个方面:“发送”。 (情绪)和“主题”。 “平均”表示情绪和主题准确性的平均分数。 “PPL”和“Dist”。分别表示困惑度和平均清晰度。括号中的分数表示双方面和单方面设置之间的性能差距。
表2展示了方法的可扩展性。当从双方面扩展到三方面时,DIST. LENS由于其联合训练策略需要重新训练。相比之下,我们的方法和PREFIX-TUNING只需要训练一个插件,然后将插件组合起来并插入到预训练模型中。不幸的是,当从三方面扩展到四方面时,由于PREFIX-TUNING的插件之间严重干扰,其控制多个方面的能力显著退化。然而,我们的方法在相对较小的训练成本下只有轻微的性能差距,显示出其高度的可扩展性。

表 2:对三方面和四方面可控文本生成的自动评估,其中模型是从双方面设置扩展的。 “# Aspects”表示方面的数量(N)。 “大道。”表示 N 个方面的平均准确率。 “已发送”、“主题”和“时态”分别表示情感、主题和时间约束的准确性。 “莱克斯。”表示词法约束的 CSR。 “ΔTime”表示从(N-1)方面设置延伸到N方面设置的训练时间。括号中的分数表示四方面和三方面设置之间的性能差距。请注意,专门用于基于属性的控制的方法(例如 DIST)。 LENS 无法处理像词法约束这样的自由形式约束。
表3显示了跨评注者一致性为0.31(Fleiss’ κ)。实验表明,我们的方法在所有三个方面的性能上都显著优于两个基线,p值小于0.01,这是通过使用一个流行的开源工具(Dror等人,2018)进行成对的自助法和t检验确定的。与自动评估不同,GEDI在情感相关性方面表现最差。这可能是因为GEDI经常生成情绪模棱两可和非流畅的句子,而人类评注者倾向于给这些句子较低的评分。其他结果与自动评估结果一致。
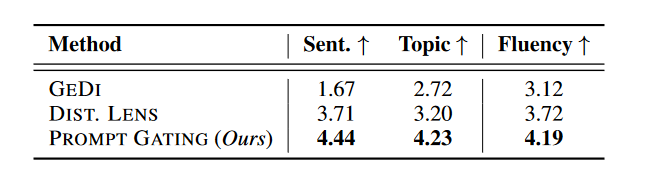
表 3:对双向可控文本生成的人类评估。每个句子根据情感和主题的相关性和流畅性评分为 1 到 5 分。
多属性受控文本翻译
数据集
为了将我们的方法与基线进行彻底比较,我们还采用了序列到序列生成任务(即机器翻译(Bahdanau et al., 2015))。实验是在 WMT14 德语 → 英语基准上进行的。我们在机器翻译中采用了三个方面的约束,标签都是从目标句子中自动获得的。我们使用关键字(Post 和 Vilar,2018)和时态(Ficler 和 Goldberg,2017)来控制翻译,就像在文本生成任务中一样。具体来说,我们采用与德语源含义相同的法语句子,这可以看作是提高翻译质量的外部知识(Zoph and Knight,2016),作为第三个约束。
评估
我们采用了SACREBLEU(Post, 2018)来计算BLEU分数(Papineni等人,2002),以评估翻译质量。类似于文本生成(§5.1),我们使用CSR(Chen等人,2020)和时态准确度分别评估词汇和时间约束。
基线
除了PROMPT-TUNING(Lester等人,2021)和PREFIX-TUNING(Li和Liang,2021)(§5.1),我们还采用了另外两种有代表性的参数高效方法作为基线:
- LORA(Hu等人,2021):这种方法在注意力子层中加入了可训练的秩分解矩阵。
- PARALLEL ADAPTER(Houlsby等人,2019):这种方法在预训练子层之间并行插入前馈子层。
与PREFIX-TUNING相似,对于LORA和PARALLEL ADAPTER,每个插件都是单独训练的,并且在推理过程中,多个插件简单地连接在一起,以适应多方面设置。
结果
表4展示了在可控机器翻译上的结果。不同于文本生成,机器翻译中的约束不仅仅包含基于属性的约束。因此,专门为基于属性的约束设计的方法无法应用于这项任务。令人惊讶的是,PROMPT-TUNING在基线中实现了最高的约束准确率和翻译质量,因为它在很大程度上保留了插件满足约束的能力。PREFIX-TUNING面临着约束准确率和BLEU分数的严重退化,这可能归因于机器翻译比文本生成具有更复杂的模型结构。我们的方法在机器翻译方面胜过所有基线,且在两项任务上的一致优势展现了其普适性。
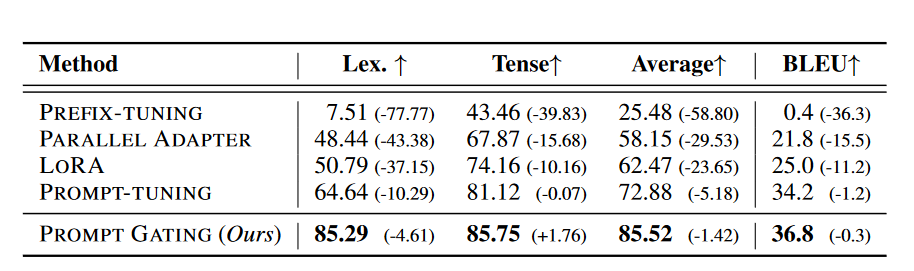
表 4:可控机器翻译结果。实验是在 WMT14 德语→英语基准上进行的。约束有三个方面:词汇约束、时态、外部知识(法语同义句)。 “Lex.”和“Tense”分别表示词汇和时间约束的 CSR 和准确性。“Average”表示它们的平均准确度。括号中的分数表示双方面和单方面设置之间的性能差距。
分析
相互干扰
类似于对PREFIX-TUNING和PROMPT-TUNING的相互干扰进行的实证分析(见§3),我们也在图2中绘制了我们方法中注入次数与相互干扰变化的关系。通过门控机制来选择性地重新缩放插件的干预,干扰的增长得到了控制。
消融实验
表5展示了剥离研究以及我们方法的变体比较。根据与变化相对应的性能差距,我们可以发现约束的文本背景略微影响约束准确率,而可训练门控的标准化是良好性能的关键点。此外,可训练门控应放置在交互刚发生的位置(即在注意力子层之后)。请参阅附录C和D了解更多结果、分析和案例。
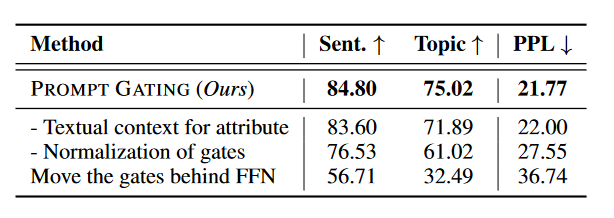
表 5:消融研究以及与我们方法的变体的比较。 “- Textual context for attribute”表示消除基于属性的约束的文本上下文(参见等式(6))。 “- Normalization of gates”表示消除对门进行归一化的 sigmoid(·) 函数(参见等式(7))。 “Move the gates behind FFN”表示可训练门应用位置的变化。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!