Python实现的二叉树的先序、中序、后序遍历示例
2023-12-14 23:18:37
一、先序、中序、后序遍历的次序:
创建好一棵二叉树后,可以按照一定的顺序对树中所有的元素进行遍历。按照先左后右,树
的遍历方法有三种:先序遍历、中序遍历和后序遍历。
其中,先序遍历的次序是:如果二叉树不为空,则访问根节点,然后访问左子树,最后访问右
子树;否则,程序退出。
中序遍历的次序是:如果二叉树不为空,则先访问左子树,然后访问根节点,最后访问右子树;
否则,程序退出。
后序遍历的次序是:如果二叉树不为空,则先访问左子树,然后访问右子树,最后访问根节点。
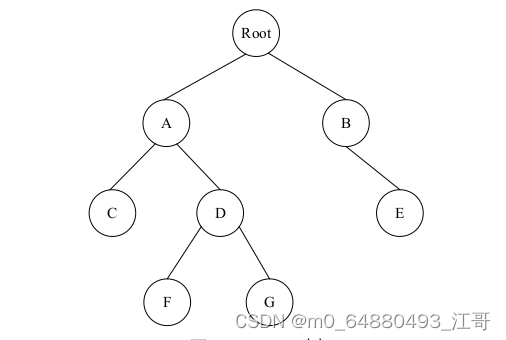
二、示例所用的二叉树图:
三、示例代码:
class BinaryTree: # 创建一个二叉树节点的类,节点中定义三个属性,
def __init__(self, elem): # 分别为 elem 本身的值,还有 lchild 左孩子和rchild 右孩子
self.elem = elem
self.lchild = None
self.rchild = None
def insert_left(self, elem): # 向左子树插入节点
self.lchild = BinaryTree(elem)
return self.lchild
def insert_right(self, elem): # 向右子树插入节点
self.rchild = BinaryTree(elem)
return self.rchild
def show(self): # 输出节点数据
print(self.elem)
def preorder(node): # 先序遍历函数
if node.elem:
node.show()
if node.lchild:
preorder(node.lchild)
if node.rchild:
preorder(node.rchild)
def inorder(node): # 中序遍历函数
if node.elem:
if node.lchild:
inorder(node.lchild)
node.show()
if node.rchild:
inorder(node.rchild)
def postorder(node): # 后序遍历函数
if node.elem:
if node.lchild:
postorder(node.lchild)
if node.rchild:
postorder(node.rchild)
node.show()
if __name__ == '__main__':
Root = BinaryTree('Root')
a = Root.insert_left('A')
c = a.insert_left('C')
d = a.insert_right('D')
f = d.insert_left('F')
g = d.insert_right('G')
b = Root.insert_right('B')
e = b.insert_right('E')
print('binary tree Pre-traversal:')
preorder(Root)
print('binary tree In-traversal:')
inorder(Root)
print('binary tree Post-traversal:')
postorder(Root)
文章来源:https://blog.csdn.net/m0_64880493/article/details/134864085
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!