4.5 A TILED MATRIX MULTIPLICATION KERNEL
我们现在准备展示一个tiled矩阵乘法内核,该内核使用共享内存来减少对全局内存的流量。图中4.16显示的内核。实施图4.15.中所示的阶段。在图4.16中,第1行和第2行声明Mds和Nds为共享内存变量。回想一下,共享内存变量的范围是一个块。因此,将为每个块创建一对Mds和Nds,并且一个块的所有线程都可以访问相同的Mds和Nds。这很重要,因为块中的所有线程都必须能够访问加载的M和N元素由同行进入Mds和Nds,以便他们可以使用这些值来满足他们的输入需求。
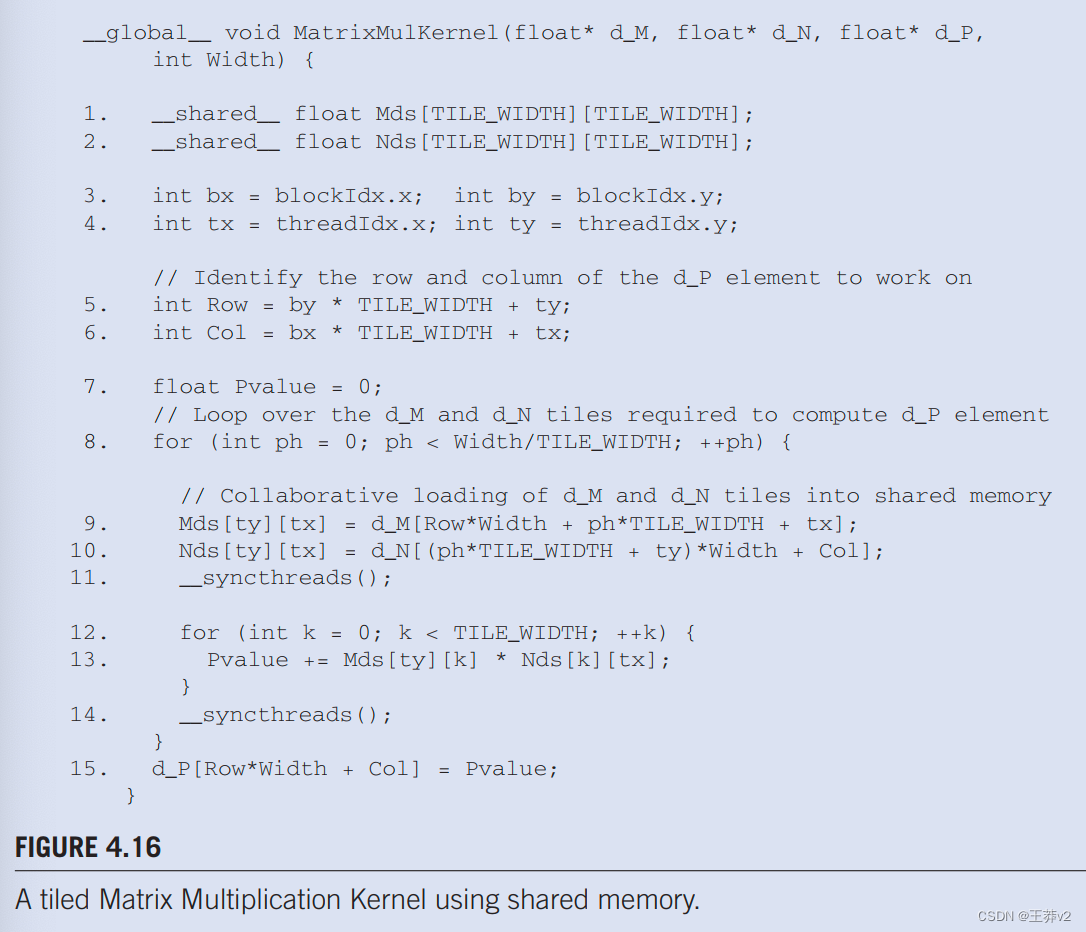
第3行和第4行将threadIdx和blockIdx值保存到自动变量中,从而保存到寄存器中,以便快速访问。回想一下,自动标量变量被放置在寄存器中。它们的范围在每个线程中;即一个tx、ty、bx和by的私有版本由运行时系统为每个线程创建,并将驻留在线程可访问的寄存器中。它们使用threadIdx和blockIdx值初始化,并在线程生命周期内多次使用。一旦线程结束,这些变量的值将不复存在。
第5行和第6行确定了线程要生成的P元素的行和列索引。该代码假设每个线程负责计算一个P元素。如第6行所示,水平(x)位置或由线程生成的P元素的列索引可以计算为bxTILE_WIDTH+ tx,因为每个块都涵盖了水平维度中的TILE_WIDTH元素。块bx中的线程在它之前会有bx线程块,或(bxTILE_WIDTH)线程;它们涵盖了P的bxTILE_WIDTH元素。同一块中的另一个tx线程将覆盖另一个tx元素。因此,带有bx和tx的线程应该负责计算x索引为bxTILE_WIDTH+ tx的P元素。这个水平索引保存在线程的变量Col中,图4.17.中也说明了。
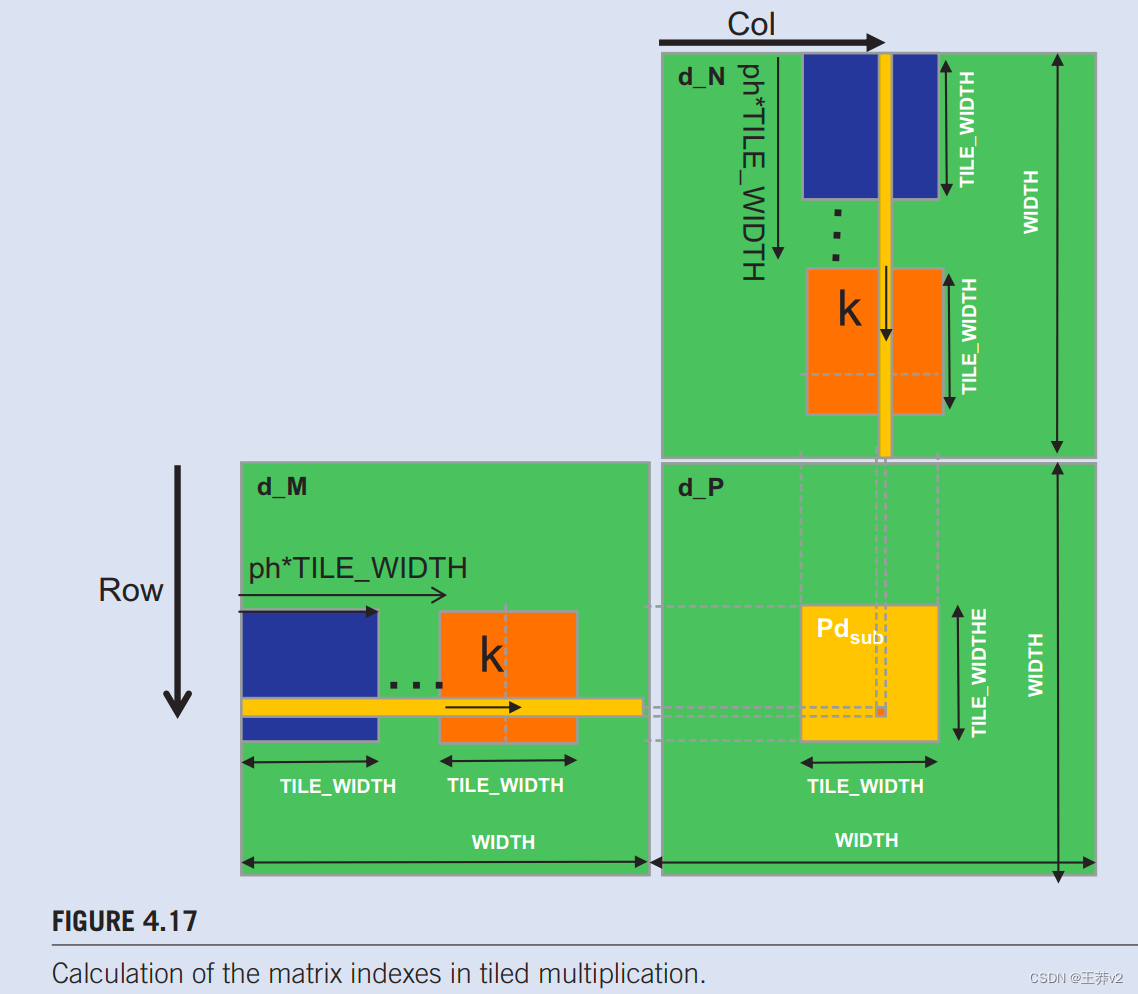
在图4.14中,由block1,0的thread0,1计算的P元素的x索引为02+ 1= 1。同样,y索引可以通过byTILE_WIDTH+ ty计算。此垂直索引保存在线程的变量行中。因此,每个线程计算Col列和Row行的P元素,如图4.17所示。.回顾图4.14中的例子,由block1,0的线程1.0计算的P元素的y索引,”为1*2+ 0=2。因此,由此线程计算的P元素是P2.1。
图4.16中的第8行。标志着循环的开始,循环贯穿计算P元素的所有阶段。循环的每个迭代都对应于图4.15.中所示计算的一个阶段。Ph变量表示点积已经完成的阶段数。每个阶段使用一个M的图块和一个N个元素的图块。因此,在每个阶段开始时,前几个阶段都处理了M和N元素的ph*TILE_WIDTH对。
在每个阶段,第9行将适当的M元素加载到共享内存中。由于我们已经知道要由线程处理的M行和N列,我们现在讨论M的列索引和N的行索引。如图4.17所示。每个区块都有TILE_WIDTH 线程将协作将TILE_ WIDTH M元素加载到共享内存中。因此,我们只需要分配每个线程来加载一个M元素,这可以使用blockldx和threadIdx方便地完成。要加载的M元素部分的起始列索引是ph*TILE_WIDTH。因此,一个简单的方法是让每个线程加载一个tx(threadldx.x值)位置远离该起点的元素。
这种情况由第9行表示,其中每个线程加载M[Rowwidth + phTILE_WIDTH + txJ,其中线性化索引与行索引行和列索引ph*TILE_WIDTH + tx形成。由于Row的值是ty的线性函数,每个TILE_WIDTH2线程都会将一个唯一的M元素加载到共享内存中。这些线程将一起加载图4.17.中M的暗方子集。读者应该使用图4.14中的示例。和图4.15验证单个线程的地址计算是否正确。
第11行中的屏障_syncthreads()确保所有线程在任何线程向前移动之前都已完成将M和N的tile加载到Mds和Nds中。然后,第12行的循环在这些tile元素的基础上执行点积的一个阶段。Thready.tx的循环进度如图4.17所示,M和N元素沿箭头的访问方向,箭头标有k,第12行的循环变量。这些元素将从Mds和Nds访问**,Mds和Nds是包含这些M和N元素的共享内存阵列**。第14行中的屏障__syncthreads()确保所有线程在进入下一个迭代并从下一个tile加载元素之前,所有线程都已完成使用共享内存中的M和N元素。通过这种方式,没有一个线程会过早地加载元素并破坏其他线程的输入值。
从8行到14行的嵌套环路说明了一种称为 strip-mining 的技术,该技术需要一个长期运行的环路并将其分阶段。每个阶段都由一个内部循环组成,该循环执行原始循环的多次连续迭代。原始循环成为一个外部循环,其作用是迭代调用内部循环,以便原始循环的所有迭代都按照原始顺序执行。通过在内部循环之前和之后添加屏障同步,我们强制同一块中的所有线程将其工作完全集中在其输入数据的一部分上。Strip mining可以通过在数据并行程序中tile来创建所需的阶段。
点积的所有阶段完成后,执行将退出第8行的循环。所有线程都通过使用线性化索引计算的 Row和Col写入其P元素。
tile算法提供了巨大的好处。对于矩阵乘法,全局内存访问减少了TILE_WIDTH的倍数。如果使用16 x 16的tile,我们可以将全局内存访问量减少16倍。这将计算与全局内存的访问率从1提高到16。这种改进允许CUDA设备的内存带宽支持接近其峰值性能的计算速率;例如,具有150 GB/s全局内存带宽的设备可以接近((150/4)*16)=600 GFLOPS!
虽然tile矩阵乘法内核的性能改进令人印象深刻,但它包括一些简化的假设。首先,假设矩阵的宽度是线程块宽度的倍数。这种假设阻止了内核正确处理任意大小的矩阵。第二个假设是矩阵是平方矩阵,这在现实生活中并不总是正确的。在下一节中,我们将介绍一个带有边界检查的内核,以消除这些假设。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!