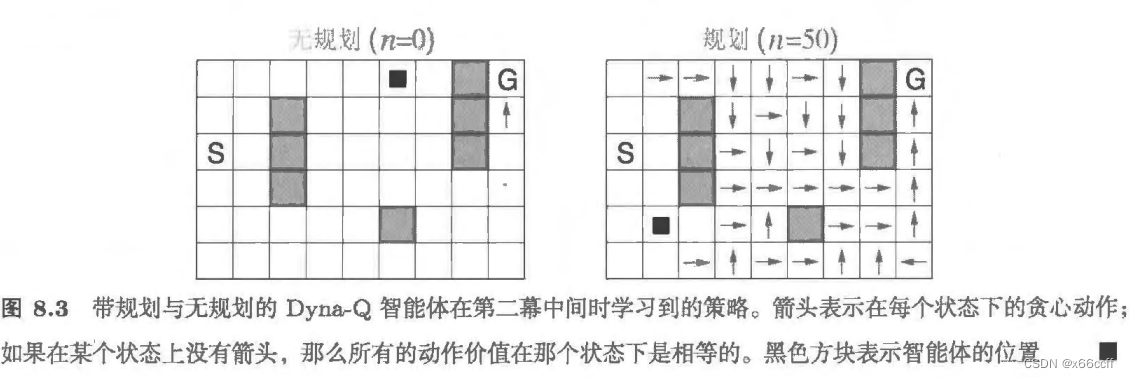
【强化学习-读书笔记】表格型有模型和无模型的结合、Dyna-Q、Dyna-Q+、表格型方法的总结

参考 
Reinforcement Learning, Second Edition  
An Introduction 
By Richard S. Sutton and Andrew G. Barto

前面的方法要么是单纯的 model-based ** 方法，要么是 model-free。基于模型的方法将规划作为其主要组成部分，而无模型的方法则主要依赖于学习**。
实际上我们可以是将基于模型的方法和无模型的方法整合起来，推广得到一个广义的学习方式。

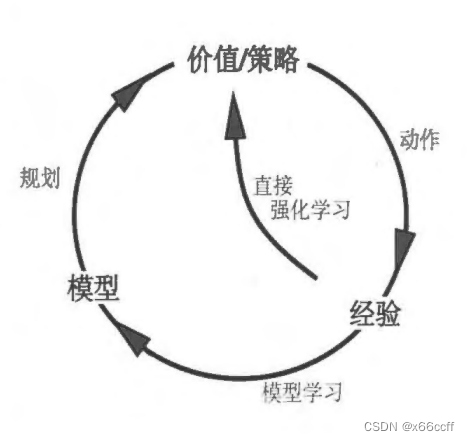
模型选择动作，从环境中得到的经验，一方面用于直接强化学习（无模型思路），另一方面这些经验同时用于环境模型的训练（有模型），然后环境模型用于规划/训练/更新价值或者策略，经验被间接的用于更新价值/策略函数 $V,Q$

间接方法往往能更充分地利用有限的经验，从而获得更好的策略，减少与环境的相互作用（例：RLHF）。
另一方面，直接方法则简单得多，它不受模型的设计偏差的影响。

Model-based : “原理认知”、“主动的预谋性规划”
Model-free：“试错学习”、“被动的反应式决策”

Dyna

一般的 Dyna 架构

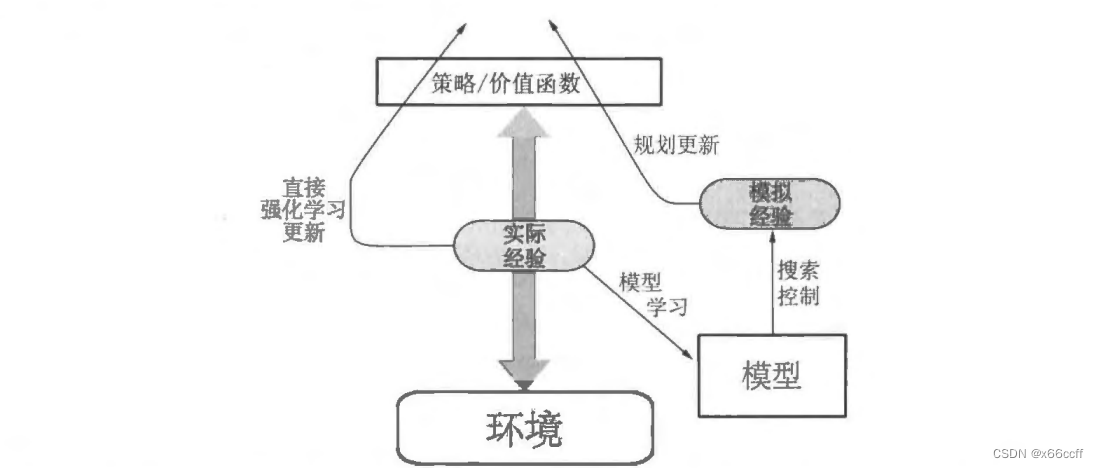
真正的经验在环境和策略之间来回传递，影响策略和价值函数，就像环境模型产生的模拟经验一样。

表格型 Dyna-Q

注意是每一步都重复$n$次，而不是每一幕，每走一步就开始（类似于）经验回放。

所以将规划和动作融合起来是很简单的，两者都以尽可能快的速度进行。智能体既是反应式的也是预谋式的，它总是立即对最新的传感信息给予反馈回应，但也同时总是在后台不断地进行规划。

考虑到很多情况下，环境的响应也是需要时间的，因此算法如果有多余的计算能力，就可以用于规划部分进行更新。Dyna-Q 里面的这个 Model 有一点像经验回放，在下棋这个场景里面，就是在下了一步棋之后，等对手下的过程中，开始通过随机回放之前自己的动作$(s,a,r,s^{\prime })$，不断更新自己的Q，等下一步开始的时候（对手行棋完毕），Q实际上已经更新了很多次了。

从走迷宫的例子分析 Dyna-Q 为什么更好

在书中的例子中， Dyna-Q 进行了 2 幕就找到了一个很不错的策略。我们从这里例子入手，分析为什么 Dyna-Q 能够这么快。

第一幕开始，
	绝大多数动作收益都是0，因此 Q <- 0，算法处于近似随机游走的状态
		每走完一步，算法进行规划更新，for 1:50 随机采样 s,a
			Q(s,a) <- 0
	直到智能体走到 G 点， Q <- 1
		for 1:50 随机采样 s,a
			Q(s,a) <- 大于0的数，if 采样到了靠近 G 点的为位置，
			这个采样概率随着更新为大于0的位置的数量增多，概率也逐渐增大，
			于是表现为箭头开始从 G 点逐渐往起点扩展，从而形成一个较优的策略
第二幕开始，
	同理，在第二幕中间就已经可以得到一个不错的策略了。

Dyna-Q+ ：用探索奖励鼓励很久没有探索过的位置

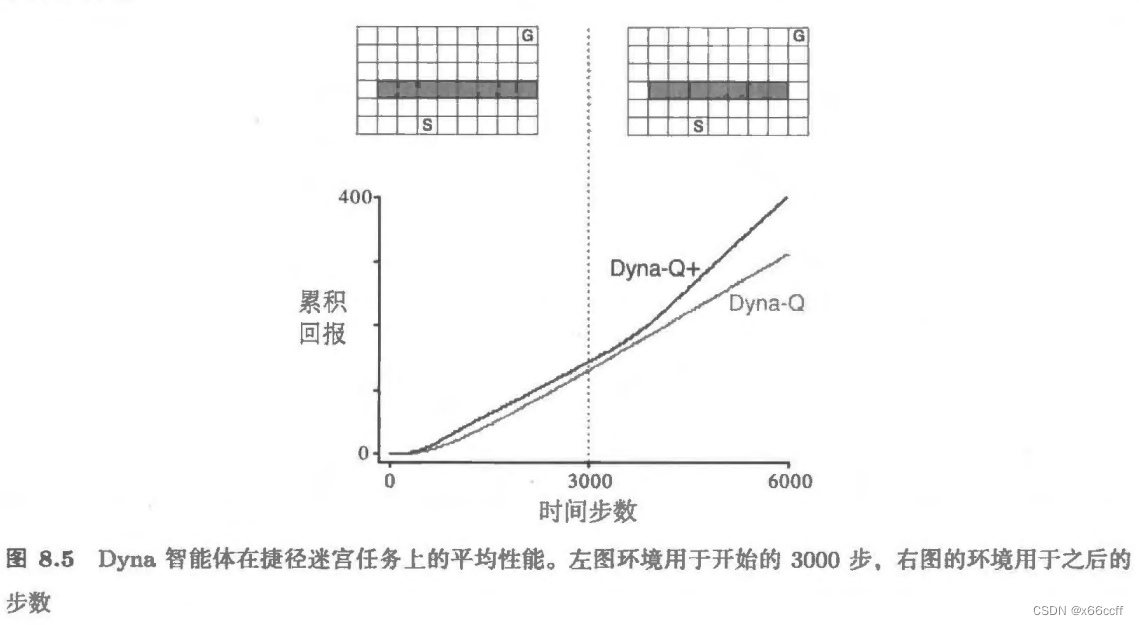
最初，最优路径绕过屏障 （左上） 然而，在 3000 步之后，沿着右侧打开一条较短路径，而它不会影响较长的路径（右上角） 图表显示，普通 Dyna-Q 不会切换到捷径。事实上，它从未意识到新路径的存在它的模型说没有捷径，所以它规划得越多，就越不可能走到右边发现它 即使使用了一个 $?$－贪心策略，智能体也不太可能采取足够大量的试探动作来发现捷径.

Dyna-Q+ 在环境不平稳的时候表现更好，因为鼓励了智能体探索很久没有探索过的地方。

Dyna-Q+为动作相关的模拟经验设置的“额外收益”将会提供给智能体。如果模型对单步转移的收益是 $r$，而这个转移在$\tau$时刻内没有被尝试，那么在更新时就会采用$r+\kappa \sqrt{r}$的收益，其中$\kappa$是一个比较小的数字。

类似于UCB，太长时间没有访问了就给额外的奖励，让模型去探索这个位置（探索路径的形成是由于一连串的需要探索的位置奖励都增加了）

总结表格型学习

其他分类标准

回报的定义 任务是分幕式还是持续性的，带折扣的还是不带折扣的？
动作价值 、状态价值还是后位状态价值 需要估计哪种价值？如果是状态价值 则在进行动作选择时，要么有一个模型 要么有个独立的策略（如“行动器－评判器”方法）
动作选择/试探 怎样进行动作选择来确保在试探和开发之间做一个合理的平衡？我们已经讨论了一些很简单的方法： $?$－贪心、价值的乐观初始化、柔性最大化、置信上界
同步还是异步 对于所有状态来说，更新是同时进行的还是按照某种顺序一个接着一个更新？
真实还是模拟仿真 更新基于真实的经验还是模拟的经验？如果两者都有，它们的比例是怎样的？
更新的位置 哪个状态或“状态－动作“ 二元组应该被更新？无模型的方法只能从真实遇到的状态和“状态 动作“二元组中进行选择，但是基于模型的方法就可以任意选择这里有很多种可能的情况
更新的时机 更新是动作选择的一部分，还是在动作选择之后进行？
更新的记忆 更新的价值应该被保存多久？它们应该被永久保存，还是像在启发式搜索中那样仅仅在动作选择期间保存？