数据结构学习 Leetcode1143最长公共子序列
2023-12-21 12:29:09
动态规划 最长公共子序列LCS
这是我在看动态规划学习的时候做的。
这是一篇LCS。LCS是两个数组进行比较。
题目:
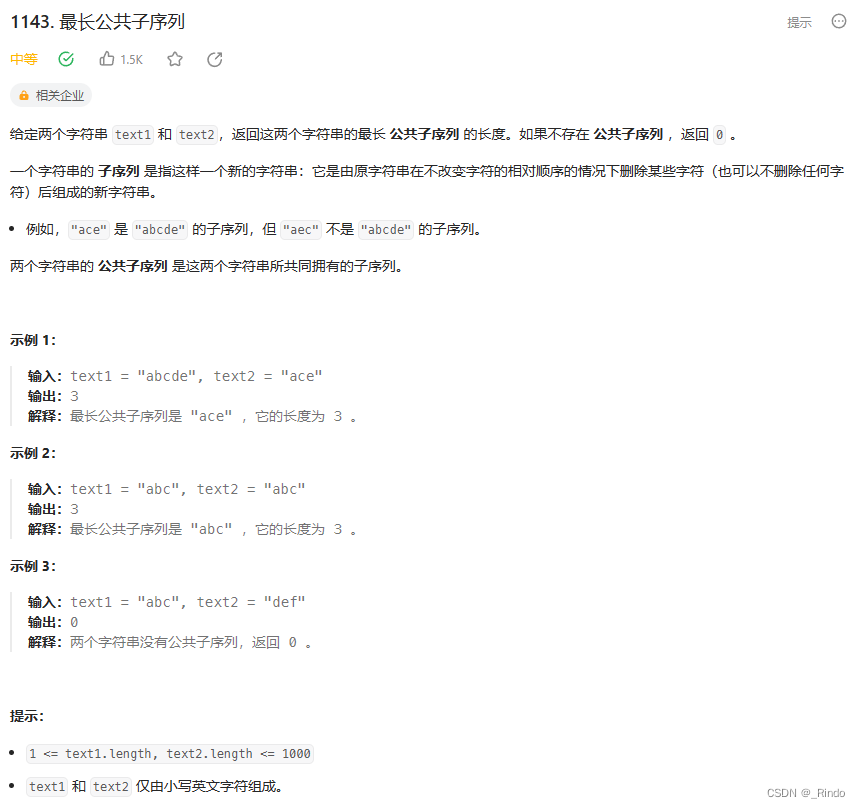
思路:
?我觉得这个总结挺好的:
求两个数组或者字符串的最长公共子序列问题,肯定是要用动态规划的。
首先,区分两个概念:子序列可以是不连续的;子数组(子字符串)需要是连续的;
另外,动态规划也是有套路的:单个数组或者字符串要用动态规划时,可以把动态规划 dp[i] 定义为 nums[0:i] 中想要求的结果;当两个数组或者字符串要用动态规划时,可以把动态规划定义成两维的?dp[i][j]?,其含义是在?A[0:i]?与?B[0:j]?之间匹配得到的想要的结果。
状态:dp[i][j]:第一个串的前i位和第二个串的前j位中的最长公共子序列
转移方程:
复杂度计算:
时间复杂度:O(nm)
空间复杂度:O(nm)
?代码:
#include <string>
#include <vector>
#include <iostream>
//动态规划
// 最长公共子序列
//时间复杂度:O(n×m)
//空间复杂度:O(n×m)
class Solution {
public:
int longestCommonSubsequence(std::string text1, std::string text2) {
std::vector<std::vector<int>> dp(text1.size(), std::vector<int>(text2.size(), 0));
for (int i = 0; i < text1.size(); ++i)
{
for (int j = 0; j < text2.size(); ++j)
{
if (text1[i] == text2[j])
dp[i][j] = (i > 0 && j > 0) ? dp[i - 1][j - 1] + 1 : 1;
else
{
int a_tmp = i > 0 ? dp[i - 1][j] : 0;
int b_tmp = j > 0 ? dp[i][j - 1] : 0;
dp[i][j] = std::max(a_tmp, b_tmp);
}
}
}
return dp[text1.size() - 1][text2.size() - 1];
}
};
void Test_solution1()
{
std::string text1{ "abceda" };
std::string text2{ "acea" };
Solution solution;
std::cout<<solution.longestCommonSubsequence(text1, text2);
}
文章来源:https://blog.csdn.net/rainssssss/article/details/135125999
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!