三次 Bezier 曲线 bern 基函数的形式

Bezier 曲线的控制多边形有 4 个控制点， $P_0$、$P_1$、$P_2$ 和 $P_3$, Bezier 曲线是三次多项式，称为三次 Bezier 曲线，

$$\begin{array}{c}P(t)=\sum _{i=0}^3{P}_i{B}_{i,3}(t)=(1?t{)}^3{P}_0+3t(1?t{)}^2{P}_1+3t^2(1?t)P_2+t^3{P}_3\end{array}\text{\hspace{1em}?}$$
$$\begin{gathered} B_{0,3}(t)=(1?t{)}^3 \\ {B}_{1,3}(t)=3t(1?t{)}^2 \\ {B}_{2,3}(t)=3t^2(1?t) \\ {B}_{3,3}(t)=t^3 \end{gathered}$$

double step = 0.01;
for (double t = 0.0; t < 1.0; t += step)
{	

	// 计算 基函数
	p.x = 0;
	p.y = 0;

	double B03 = (1 - t) * (1 - t) * (1 - t);
	double B13 = 3 * t * (1 - t) * (1 - t);
	double B23 = 3 * t * t * (1 - t);
	double B33 = t * t * t;

	p.x += B03 * P[0].x + B13 * P[1].x + B23 * P[2].x + B33 * P[3].x;
	p.y += B03 * P[0].y + B13 * P[1].y + B23 * P[2].y + B33 * P[3].y;

	//pDC->LineTo(ROUND(p.x), ROUND(p.y));
}

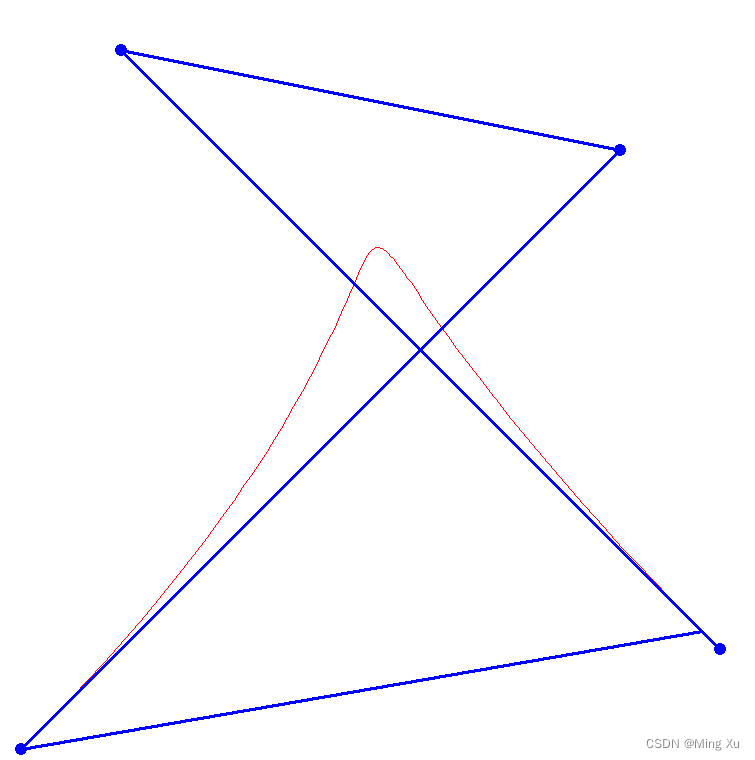
参考 《计算几何算法与实现》孔令德