吴恩达深度学习l2week2编程作业—Optimization Methods(最新中文跑通版)
到目前为止,您一直使用渐变下降来更新参数并将成本降至最低。在本笔记本中,您将获得一些更先进的优化方法的技能,这些方法可以加快学习速度,甚至可能使您获得更好的成本函数最终值。拥有一个好的优化算法可能是等待几天与只需几个小时就能获得好结果的区别。
到此笔记本结束时,您将能够:
- 运用优化算法例如Gradient Descent,Momentum,RMSprop,Adam
- 使用随机迷你批次加速收敛并改进优化
梯度下降在成本函数𝐽上“走下坡路”。可以将其视为尝试这样做:

在训练的每一步,你都会按照特定的方向更新你的参数,试图达到尽可能低的点。
![]()
让我们跟着吴恩达大佬的步伐开始吧!
1.导入packages
import numpy as np
import matplotlib.pyplot as plt
import scipy.io
import math
import sklearn
import sklearn.datasets
from opt_utils_v1a import load_params_and_grads, initialize_parameters, forward_propagation, backward_propagation
from opt_utils_v1a import compute_cost, predict, predict_dec, plot_decision_boundary, load_dataset
from copy import deepcopy
from testCases import *
from public_tests import *
%matplotlib inline
plt.rcParams['figure.figsize'] = (7.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
%load_ext autoreload
%autoreload 22.梯度下降Gradient Descent
机器学习中一种简单的优化方法是梯度下降(GD)。我们每一次循环都是对整个训练集进行学习,这叫做批量梯度下降(Batch Gradient Descent),我们之前说过了最核心的参数更新的公式,这里我们再来看一下:

L是层数 ;𝛼是学习率
Exercise 1 - update_parameters_with_gd
def update_parameters_with_gd(parameters, grads, learning_rate):
"""
parameters——包含要更新的参数的python字典:
parameters['W'+str(l)]=Wl
parameters['b'+str(l)]=bl
grades——包含梯度的python字典,用于更新每个参数:
梯度['dW'+str(l)]=dWl
梯度['db'+str(l)]=dbl
learning_rate——学习速率,标量。
返回parameters——包含更新参数的python字典
"""
for l in range(L):
parameters["W" + str(l +1)] = parameters["W" + str(l + 1)] - learning_rate * grads["dW" + str(l + 1)]
parameters["b" + str(l +1)] = parameters["b" + str(l + 1)] - learning_rate * grads["db" + str(l + 1)]
return parameters
parameters, grads, learning_rate = update_parameters_with_gd_test_case()
learning_rate = 0.01
parameters = update_parameters_with_gd(parameters, grads, learning_rate)
print("W1 =\n" + str(parameters["W1"]))
print("b1 =\n" + str(parameters["b1"]))
print("W2 =\n" + str(parameters["W2"]))
print("b2 =\n" + str(parameters["b2"]))
update_parameters_with_gd_test(update_parameters_with_gd)
其中的一个变体是随机梯度下降(SGD),它相当于小批量梯度下降,其中每个小批量只有一个例子。您刚刚实现的更新规则不会更改。改变的是,一次只计算一个训练示例的梯度,而不是整个训练集的梯度。下面的代码示例说明了随机梯度下降和批量梯度下降之间的区别。
- 批量梯度下降
X = data_input
Y = labels
m = X.shape[1] # Number of training examples
parameters = initialize_parameters(layers_dims)
for i in range(0, num_iterations):
# Forward propagation
a, caches = forward_propagation(X, parameters)
# Compute cost
cost_total = compute_cost(a, Y) # Cost for m training examples
# Backward propagation
grads = backward_propagation(a, caches, parameters)
# Update parameters
parameters = update_parameters(parameters, grads)
# Compute average cost
cost_avg = cost_total / m- 随机梯度下降
X = data_input
Y = labels
m = X.shape[1] # Number of training examples
parameters = initialize_parameters(layers_dims)
for i in range(0, num_iterations):
cost_total = 0
for j in range(0, m):
# Forward propagation
a, caches = forward_propagation(X[:,j], parameters)
# Compute cost
cost_total += compute_cost(a, Y[:,j]) # Cost for one training example
# Backward propagation
grads = backward_propagation(a, caches, parameters)
# Update parameters
parameters = update_parameters(parameters, grads)
# Compute average cost
cost_avg = cost_total / m在随机梯度下降算法中,每次迭代中仅使用其中一个样本,当训练集很大时,使用随机梯度下降算法的运行速度会很快,但是会存在一定的波动。
在随机梯度下降中,在更新梯度之前,只使用1个训练样本。 当训练集较大时,随机梯度下降可以更快,但是参数会向最小值摆动,而不是平稳地收敛,我们来看一下比较图:
还要注意,实现SGD总共需要3个for循环:
- 遍历迭代次数
- 遍历m个训练样本
- 遍历层数
在实际中,更好的方法是使用小批量(mini-batch)梯度下降法,小批量梯度下降法是一种综合了梯度下降法和随机梯度下降法的方法,在它的每次迭代中,既不是选择全部的数据来学习,也不是选择一个样本来学习,而是把所有的数据集分割为一小块一小块的来学习,它会随机选择一小块(mini-batch),块大小一般为。一方面,充分利用的GPU的并行性,更一方面,不会让计算时间特别长,来看一下比较图:

3.Mini-Batch梯度下降
使用mini-batch要经过两个步骤:
- 把训练集打乱,但是X和Y依旧是一一对应的,之后,X的第i列是与Y中的第i个标签对应的样本。乱序步骤确保将样本被随机分成不同的小批次。如下图,X和Y的每一列代表一个样本
- 切分,我们把训练集打乱之后,我们就可以对它进行切分了。这里切分的大小是64,如下图:


Exercise 2 - random_mini_batches
实施random_mini_batches
#经历完打乱,分割后
#第一个mini-batch
first_mini_batch_X = shuffled_X[:, 0 : mini_batch_size]
#第二个mini-batch
second_mini_batch_X = shuffled_X[:, mini_batch_size : 2 * mini_batch_size]
...
...
请注意,最后一个小批量最终可能小于mini_batch_size=64。
让?𝑠? 表示s向下取整到最接近的整数(这是Python中的math.floor(s))。如果示例的总数不是mini_batch_size=64的倍数,则将存在??
完整64个实例的小批量,最终小批量中的实例数量为?m? -? mini_batch_size* ???

使用for循环变量k可以帮助以mini_batch_size的倍数递增i和j。
例如,如果要以3的倍数递增,可以执行以下操作:
n = 3
for k in (0 , 5):
print(k * n)# GRADED FUNCTION: random_mini_batches
def random_mini_batches(X, Y, mini_batch_size = 64, seed = 0):
"""
从(X,Y)中创建一个随机的mini-batch列表
X - 输入数据,维度为(输入节点数量,样本的数量)
Y - 对应的是X的标签(1对应蓝点|0对应红点),维度为(1,样本的数量)
mini_batch_size - 每个mini-batch的样本数量
返回
mini-bacthes - 一个同步列表,维度为(mini_batch_X,mini_batch_Y)
"""
np.random.seed(seed)
m = X.shape[1] # 训练样本数
mini_batches = []
#第一步:打乱顺序
permutation = list(np.random.permutation(m)) #它会返回一个长度为m的随机数组,且里面的数是0到m-1
shuffled_X = X[:,permutation] #将每一列的数据按permutation的顺序来重新排列。
shuffled_Y = Y[:,permutation].reshape((1,m))
inc = mini_batch_size
#第二步,分割
#仅具有完整小批量大小的案例,即64个实例中的每一个。
num_complete_minibatches = math.floor(m / mini_batch_size) #把你的训练集分割成多少份,请注意,如果值是99.99,那么返回值是99,剩下的0.99会被舍弃
for k in range(0,num_complete_minibatches):
mini_batch_X = shuffled_X[:,k * mini_batch_size:(k+1)*mini_batch_size]
mini_batch_Y = shuffled_Y[:,k * mini_batch_size:(k+1)*mini_batch_size]
mini_batch = (mini_batch_X, mini_batch_Y)
mini_batches.append(mini_batch)
#如果训练集的大小刚好是mini_batch_size的整数倍,那么这里已经处理完了
#如果训练集的大小不是mini_batch_size的整数倍,那么最后肯定会剩下一些,我们要把它处理了
if m % mini_batch_size != 0:
#获取最后剩余的部分
mini_batch_X = shuffled_X[:,mini_batch_size * num_complete_minibatches:]
mini_batch_Y = shuffled_Y[:,mini_batch_size * num_complete_minibatches:]
mini_batch = (mini_batch_X,mini_batch_Y)
mini_batches.append(mini_batch)
return mini_batchesnp.random.seed(1)
mini_batch_size = 64
nx = 12288
m = 148
X = np.array([x for x in range(nx * m)]).reshape((m, nx)).T
Y = np.random.randn(1, m) < 0.5
mini_batches = random_mini_batches(X, Y, mini_batch_size)
n_batches = len(mini_batches)
assert n_batches == math.ceil(m / mini_batch_size), f"Wrong number of mini batches. {n_batches} != {math.ceil(m / mini_batch_size)}"
for k in range(n_batches - 1):
assert mini_batches[k][0].shape == (nx, mini_batch_size), f"Wrong shape in {k} mini batch for X"
assert mini_batches[k][1].shape == (1, mini_batch_size), f"Wrong shape in {k} mini batch for Y"
assert np.sum(np.sum(mini_batches[k][0] - mini_batches[k][0][0], axis=0)) == ((nx * (nx - 1) / 2 ) * mini_batch_size), "Wrong values. It happens if the order of X rows(features) changes"
if ( m % mini_batch_size > 0):
assert mini_batches[n_batches - 1][0].shape == (nx, m % mini_batch_size), f"Wrong shape in the last minibatch. {mini_batches[n_batches - 1][0].shape} != {(nx, m % mini_batch_size)}"
assert np.allclose(mini_batches[0][0][0][0:3], [294912, 86016, 454656]), "Wrong values. Check the indexes used to form the mini batches"
assert np.allclose(mini_batches[-1][0][-1][0:3], [1425407, 1769471, 897023]), "Wrong values. Check the indexes used to form the mini batches"
print("\033[92mAll tests passed!")t_X, t_Y, mini_batch_size = random_mini_batches_test_case()
mini_batches = random_mini_batches(t_X, t_Y, mini_batch_size)
print ("shape of the 1st mini_batch_X: " + str(mini_batches[0][0].shape))
print ("shape of the 2nd mini_batch_X: " + str(mini_batches[1][0].shape))
print ("shape of the 3rd mini_batch_X: " + str(mini_batches[2][0].shape))
print ("shape of the 1st mini_batch_Y: " + str(mini_batches[0][1].shape))
print ("shape of the 2nd mini_batch_Y: " + str(mini_batches[1][1].shape))
print ("shape of the 3rd mini_batch_Y: " + str(mini_batches[2][1].shape))
print ("mini batch sanity check: " + str(mini_batches[0][0][0][0:3]))
random_mini_batches_test(random_mini_batches)shape of the 1st mini_batch_X: (12288, 64)
shape of the 2nd mini_batch_X: (12288, 64)
shape of the 3rd mini_batch_X: (12288, 20)
shape of the 1st mini_batch_Y: (1, 64)
shape of the 2nd mini_batch_Y: (1, 64)
shape of the 3rd mini_batch_Y: (1, 20)
mini batch sanity check: [ 0.90085595 -0.7612069 0.2344157 ]
All tests passed.
- Shuffling和Partitioning是构建小批量所需的两个步骤
- 二的幂常常被选择为小批量大小,例如16、32、64、128。
4.Momentum
由于小批量梯度下降只看到了一个子集的参数更新,更新的方向有一定的差异,所以小批量梯度下降的路径将“振荡地”走向收敛,使用动量可以减少这些振荡,动量考虑了过去的梯度以平滑更新, 我们将把以前梯度的方向存储在变量v中,从形式上讲,这将是前面的梯度的指数加权平均值。我们也可以把V看作是滚下坡的速度,根据山坡的坡度建立动量。我们来看一下下面的图:
Exercise 3 - initialize_velocity
初始化速度。速度,𝑣, 是一个python字典,需要使用零数组进行初始化。它的关键字与grads字典中的关键字相同,即:

既然我们要影响梯度的方向,而梯度需要使用到dW和db
# GRADED FUNCTION: initialize_velocity
def initialize_velocity(parameters):
"""
初始化速度,velocity是一个字典:
- keys: "dW1", "db1", ..., "dWL", "dbL"
- values:与相应的梯度/参数维度相同的值为零的矩阵。
参数:
parameters - 一个字典,包含了以下参数:
parameters["W" + str(l)] = Wl
parameters["b" + str(l)] = bl
返回:
v - 一个字典变量,包含了以下参数:
v["dW" + str(l)] = dWl的速度
v["db" + str(l)] = dbl的速度
"""
L = len(parameters) // 2 #神经网络的层数
v = {}
for l in range(L):
v["dW" + str(l + 1)] = np.zeros_like(parameters["W" + str(l + 1)])
v["db" + str(l + 1)] = np.zeros_like(parameters["b" + str(l + 1)])
return vparameters = initialize_velocity_test_case()
v = initialize_velocity(parameters)
print("v[\"dW1\"] =\n" + str(v["dW1"]))
print("v[\"db1\"] =\n" + str(v["db1"]))
print("v[\"dW2\"] =\n" + str(v["dW2"]))
print("v[\"db2\"] =\n" + str(v["db2"]))
initialize_velocity_test(initialize_velocity)
Exercise 4 - update_parameters_with_momentum

l:当前神经网络的层数
β:动量,是一个实数
α:学习率
def update_parameters_with_momentun(parameters,grads,v,beta,learning_rate):
"""
使用动量更新参数
参数:
parameters - 一个字典类型的变量,包含了以下字段:
parameters["W" + str(l)] = Wl
parameters["b" + str(l)] = bl
grads - 一个包含梯度值的字典变量,具有以下字段:
grads["dW" + str(l)] = dWl
grads["db" + str(l)] = dbl
v - 包含当前速度的字典变量,具有以下字段:
v["dW" + str(l)] = ...
v["db" + str(l)] = ...
beta - 超参数,动量,实数
learning_rate - 学习率,实数
返回:
parameters - 更新后的参数字典
v - 包含了更新后的速度变量
"""
L = len(parameters) // 2
# Momentum update for each parameter
for l in range(1, L + 1):
v["dW" + str(l)] = beta * v["dW" + str(l)] + (1 - beta) * grads["dW" + str(l)]
v["db" + str(l)] = beta * v["db" + str(l)] + (1 - beta) * grads["db" + str(l)]
# update parameters
parameters["W" + str(l)] = parameters["W" + str(l)] - learning_rate * v["dW" + str(l)]
parameters["b" + str(l)] = parameters["b" + str(l)] - learning_rate * v["db" + str(l)]
return parameters, vparameters, grads, v = update_parameters_with_momentum_test_case()
parameters, v = update_parameters_with_momentum(parameters, grads, v, beta = 0.9, learning_rate = 0.01)
print("W1 = \n" + str(parameters["W1"]))
print("b1 = \n" + str(parameters["b1"]))
print("W2 = \n" + str(parameters["W2"]))
print("b2 = \n" + str(parameters["b2"]))
print("v[\"dW1\"] = \n" + str(v["dW1"]))
print("v[\"db1\"] = \n" + str(v["db1"]))
print("v[\"dW2\"] = \n" + str(v["dW2"]))
print("v[\"db2\"] = v" + str(v["db2"]))
update_parameters_with_momentum_test(update_parameters_with_momentum)
需要注意的是速度v 是用0来初始化的,因此,该算法需要经过几次迭代才能把速度提升上来并开始跨越更大步伐。当beta=0时,该算法相当于是没有使用momentum算法的标准的梯度下降算法。当beta越大的时候,说明平滑的作用越明显。0.8-0.99是对于beta正常的范围,通常0.9是比较合适的值。那如何才能在开始的时候就保持很快的速度向最小误差那里前进呢?我们来看看下面的Adam算法。
5.Adam
Adam算法是训练神经网络中最有效的算法之一,它是RMSProp算法与Momentum算法的结合体。我们来看看它都干了些什么吧~
- 计算以前的梯度的指数加权平均值,并将其存储在变量v(偏差校正前)和
(偏差校正后)中。
- 计算以前梯度的平方的指数加权平均值,并将其存储在变量s(偏差校正前)和
(偏差校正后)中。
- 根据1和2更新参数。
for l = 1...L:

t?:当前迭代的次数
l:当前神经网络的层数
beta1 和 beta2:控制两个指数加权平均值的超参数
α?:学习率
ε:一个非常小的数,用于避免除零操作,一般为
Exercise 5 - initialize_adam

def initialize_adam(parameters):
"""
初始化v和s,它们都是字典类型的变量,都包含了以下字段:
- keys: "dW1", "db1", ..., "dWL", "dbL"
- values:与对应的梯度/参数相同维度的值为零的numpy矩阵
参数:
parameters - 包含了以下参数的字典变量:
parameters["W" + str(l)] = Wl
parameters["b" + str(l)] = bl
返回:
v - 包含梯度的指数加权平均值,字段如下:
v["dW" + str(l)] = ...
v["db" + str(l)] = ...
s - 包含平方梯度的指数加权平均值,字段如下:
s["dW" + str(l)] = ...
s["db" + str(l)] = ...
"""
L = len(parameters) // 2 # number of layers in the neural networks
v = {}
s = {}
for l in range(1, L + 1):
v["dW" + str(l)] = np.zeros_like(parameters["W" + str(l)])
v["db" + str(l)] = np.zeros_like(parameters["b" + str(l)])
s["dW" + str(l)] = np.zeros_like(parameters["W" + str(l)])
s["db" + str(l)] = np.zeros_like(parameters["b" + str(l)])
return v, sparameters = initialize_adam_test_case()
v, s = initialize_adam(parameters)
print("v[\"dW1\"] = \n" + str(v["dW1"]))
print("v[\"db1\"] = \n" + str(v["db1"]))
print("v[\"dW2\"] = \n" + str(v["dW2"]))
print("v[\"db2\"] = \n" + str(v["db2"]))
print("s[\"dW1\"] = \n" + str(s["dW1"]))
print("s[\"db1\"] = \n" + str(s["db1"]))
print("s[\"dW2\"] = \n" + str(s["dW2"]))
print("s[\"db2\"] = \n" + str(s["db2"]))
initialize_adam_test(initialize_adam)
Exercise 6 - update_parameters_with_adam

def update_parameters_with_adam(parameters,grads,v,s,t,learning_rate=0.01,beta1=0.9,beta2=0.999,epsilon=1e-8):
"""
使用Adam更新参数
参数:
parameters - 包含了以下字段的字典:
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
grads - 包含了梯度值的字典,有以下key值:
grads['dW' + str(l)] = dWl
grads['db' + str(l)] = dbl
v - Adam的变量,第一个梯度的移动平均值,是一个字典类型的变量
s - Adam的变量,平方梯度的移动平均值,是一个字典类型的变量
t - 当前迭代的次数
learning_rate - 学习率
beta1 - 动量,超参数,用于第一阶段,使得曲线的Y值不从0开始(参见天气数据的那个图)
beta2 - RMSprop的一个参数,超参数
epsilon - 防止除零操作(分母为0)
返回:
parameters - 更新后的参数
v - 第一个梯度的移动平均值,是一个字典类型的变量
s - 平方梯度的移动平均值,是一个字典类型的变量
"""
L = len(parameters) // 2
v_corrected = {} #偏差修正后的值
s_corrected = {} #偏差修正后的值
for l in range(1, L + 1):
v["dW" + str(l)] = beta1 * v["dW" + str(l)] + (1 - beta1) * grads["dW" + str(l)]
v["db" + str(l)] = beta1 * v["db" + str(l)] + (1 - beta1) * grads["db" + str(l)]
v_corrected["dW" + str(l)] = v["dW" + str(l)] / (1 - np.power(beta1, t))
v_corrected["db" + str(l)] = v["db" + str(l)] / (1 - np.power(beta1, t))
s["dW" + str(l)] = beta2 * s["dW" + str(l)] + (1 - beta2) * np.square(grads["dW" + str(l)])
s["db" + str(l)] = beta2 * s["db" + str(l)] + (1 - beta2) * np.square(grads["db" + str(l)])
s_corrected["dW" + str(l)] = s["dW" + str(l)] / (1 - np.power(beta2, t))
s_corrected["db" + str(l)] = s["db" + str(l)] / (1 - np.power(beta2, t))
parameters["W" + str(l)] = parameters["W" + str(l)] - learning_rate * (v_corrected["dW" + str(l)] / (np.sqrt(s_corrected["dW" + str(l)]) + epsilon))
parameters["b" + str(l)] = parameters["b" + str(l)] - learning_rate * (v_corrected["db" + str(l)] / (np.sqrt(s_corrected["db" + str(l)]) + epsilon))
return parameters, v, s, v_corrected, s_correctedparametersi, grads, vi, si, t, learning_rate, beta1, beta2, epsilon = update_parameters_with_adam_test_case()
parameters, v, s, vc, sc = update_parameters_with_adam(parametersi, grads, vi, si, t, learning_rate, beta1, beta2, epsilon)
print(f"W1 = \n{parameters['W1']}")
print(f"W2 = \n{parameters['W2']}")
print(f"b1 = \n{parameters['b1']}")
print(f"b2 = \n{parameters['b2']}")
update_parameters_with_adam_test(update_parameters_with_adam)
6.具有不同优化算法的模型
下面,您将使用以下“moons”数据集来测试不同的优化方法。(该数据集被命名为“月亮”,因为这两个类别的数据看起来都有点像新月。)
train_X, train_Y = load_dataset()

def model(X,Y,layers_dims,optimizer,learning_rate=0.0007,
mini_batch_size=64,beta=0.9,beta1=0.9,beta2=0.999,
epsilon=1e-8,num_epochs=10000,print_cost=True,is_plot=True):
"""
可以运行在不同优化器模式下的3层神经网络模型。
参数:
X - 输入数据,维度为(2,输入的数据集里面样本数量)
Y - 与X对应的标签
layers_dims - 包含层数和节点数量的列表
optimizer - 字符串类型的参数,用于选择优化类型,【 "gd" | "momentum" | "adam" 】
learning_rate - 学习率
mini_batch_size - 每个小批量数据集的大小
beta - 用于动量优化的一个超参数
beta1 - 用于计算梯度后的指数衰减的估计的超参数
beta1 - 用于计算平方梯度后的指数衰减的估计的超参数
epsilon - 用于在Adam中避免除零操作的超参数,一般不更改
num_epochs - 整个训练集的遍历次数,(视频2.9学习率衰减,1分55秒处,视频中称作“代”),相当于之前的num_iteration
print_cost - 是否打印误差值,每遍历1000次数据集打印一次,但是每100次记录一个误差值,又称每1000代打印一次
is_plot - 是否绘制出曲线图
返回:
parameters - 包含了学习后的参数
"""
L = len(layers_dims)
costs = []
t = 0 #每学习完一个minibatch就增加1
seed = 10 #随机种子
#初始化参数
parameters = opt_utils.initialize_parameters(layers_dims)
#选择优化器
if optimizer == "gd":
pass #不使用任何优化器,直接使用梯度下降法
elif optimizer == "momentum":
v = initialize_velocity(parameters) #使用动量
elif optimizer == "adam":
v, s = initialize_adam(parameters)#使用Adam优化
else:
print("optimizer参数错误,程序退出。")
exit(1)
#开始学习
for i in range(num_epochs):
#定义随机 minibatches,我们在每次遍历数据集之后增加种子以重新排列数据集,使每次数据的顺序都不同
seed = seed + 1
minibatches = random_mini_batches(X,Y,mini_batch_size,seed)
for minibatch in minibatches:
#选择一个minibatch
(minibatch_X,minibatch_Y) = minibatch
#前向传播
A3 , cache = opt_utils.forward_propagation(minibatch_X,parameters)
#计算误差
cost = opt_utils.compute_cost(A3 , minibatch_Y)
#反向传播
grads = opt_utils.backward_propagation(minibatch_X,minibatch_Y,cache)
#更新参数
if optimizer == "gd":
parameters = update_parameters_with_gd(parameters,grads,learning_rate)
elif optimizer == "momentum":
parameters, v = update_parameters_with_momentun(parameters,grads,v,beta,learning_rate)
elif optimizer == "adam":
t = t + 1
parameters , v , s = update_parameters_with_adam(parameters,grads,v,s,t,learning_rate,beta1,beta2,epsilon)
#记录误差值
if i % 100 == 0:
costs.append(cost)
#是否打印误差值
if print_cost and i % 1000 == 0:
print("第" + str(i) + "次遍历整个数据集,当前误差值:" + str(cost))
#是否绘制曲线图
if is_plot:
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('epochs (per 100)')
plt.title("Learning rate = " + str(learning_rate))
plt.show()
return parameters6.1Mini-Batch梯度下降
# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, optimizer = "gd")
# Predict
predictions = predict(train_X, train_Y, parameters)
# Plot decision boundary
plt.title("Model with Gradient Descent optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
6.2带有Momentum的Mini-Batch梯度下降
接下来,运行以下代码来查看模型如何处理动量。因为这个例子相对简单,所以使用动量的gains很小,但对于更复杂的问题,你可能会看到更大的gains。
# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, beta = 0.9, optimizer = "momentum")
# Predict
predictions = predict(train_X, train_Y, parameters)
# Plot decision boundary
plt.title("Model with Momentum optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)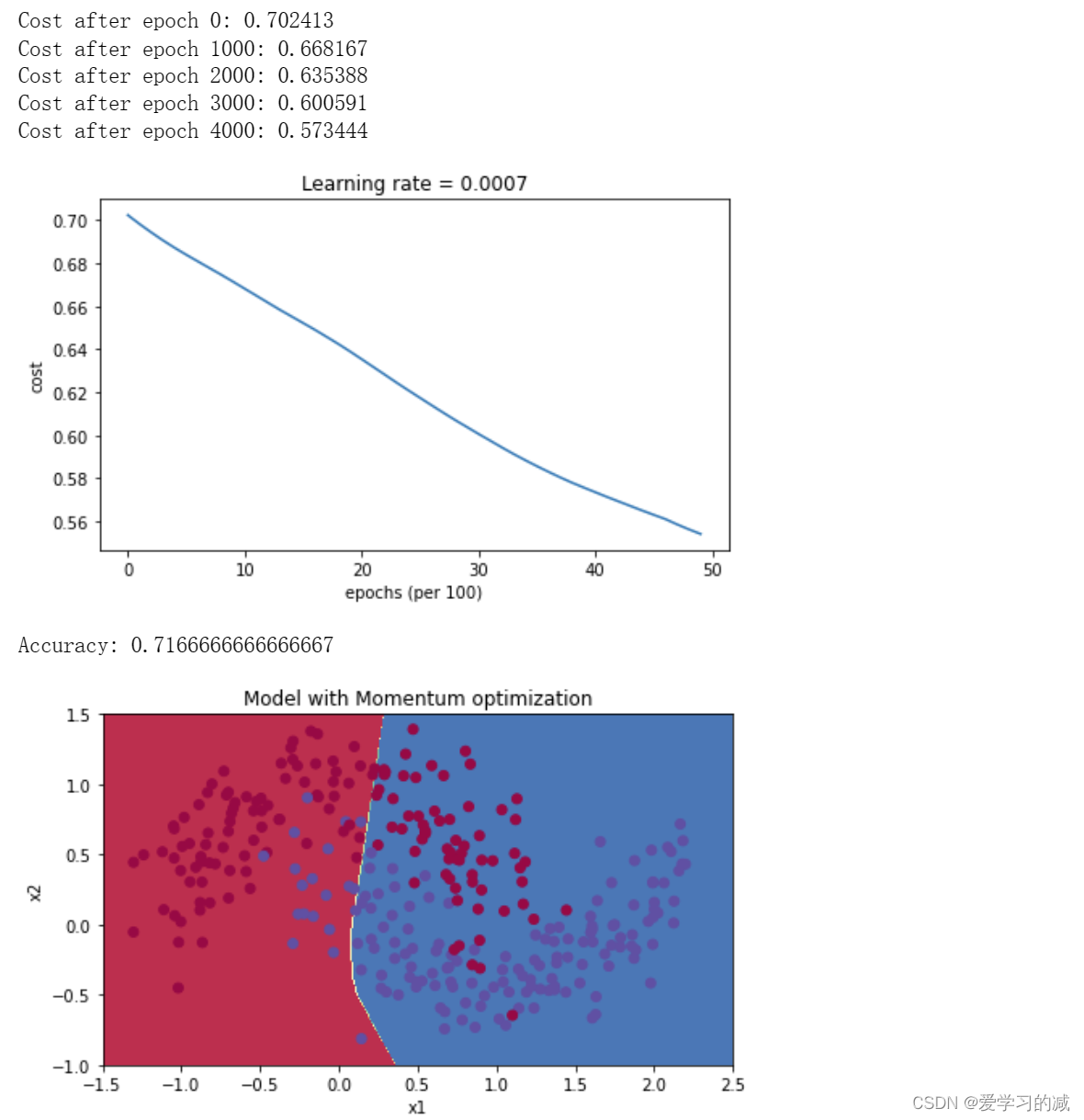
6.3用Adam的Mini-Batch梯度下降
# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, optimizer = "adam")
# Predict
predictions = predict(train_X, train_Y, parameters)
# Plot decision boundary
plt.title("Model with Adam optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
6.4总结

具有动量的梯度下降通常可以有很好的效果,但由于小的学习速率和简单的数据集所以它的影响几乎是轻微的。另一方面,Adam明显优于小批量梯度下降和具有动量的梯度下降,如果在这个简单的模型上运行更多时间的数据集,这三种方法都会产生非常好的结果,然而,我们已经看到Adam收敛得更快。Adam的一些优点包括相对较低的内存要求(虽然比梯度下降和动量下降更高)和通常运作良好,即使对参数进行微调(除了学习率α)
7.学习率衰退与进度安排
最后,学习率是另一个可以帮助你加快学习速度的超参数。
在训练的第一部分,你的模型可以大踏步前进,但随着时间的推移,使用固定的学习率α值可能会导致你的模型陷入一个永远不会完全收敛的大范围振荡中。但是,如果你要随着时间的推移慢慢降低你的学习率α,那么你可以采取更小、更慢的步骤,使你更接近最低水平。这就是学习率衰减背后的思想。
学习率衰减可以通过使用自适应方法或预定义的学习率时间表来实现。
现在,您将以三种不同的优化器模式将计划学习率衰减应用于三层神经网络,并了解每种模式的不同之处,以及不同时期的调度效果。
这个模型与你之前使用的模型基本相同,只是在这个模型中你可以包括学习率衰减。它包括两个新的参数,衰变和衰变率。
def model(X, Y, layers_dims, optimizer, learning_rate = 0.0007, mini_batch_size = 64, beta = 0.9,
beta1 = 0.9, beta2 = 0.999, epsilon = 1e-8, num_epochs = 5000, print_cost = True, decay=None, decay_rate=1):
L = len(layers_dims) # number of layers in the neural networks
costs = [] # to keep track of the cost
t = 0 # initializing the counter required for Adam update
seed = 10 # For grading purposes, so that your "random" minibatches are the same as ours
m = X.shape[1] # number of training examples
lr_rates = []
learning_rate0 = learning_rate # the original learning rate
# Initialize parameters
parameters = initialize_parameters(layers_dims)
# Initialize the optimizer
if optimizer == "gd":
pass # no initialization required for gradient descent
elif optimizer == "momentum":
v = initialize_velocity(parameters)
elif optimizer == "adam":
v, s = initialize_adam(parameters)
# Optimization loop
for i in range(num_epochs):
# Define the random minibatches. We increment the seed to reshuffle differently the dataset after each epoch
seed = seed + 1
minibatches = random_mini_batches(X, Y, mini_batch_size, seed)
cost_total = 0
for minibatch in minibatches:
# Select a minibatch
(minibatch_X, minibatch_Y) = minibatch
# Forward propagation
a3, caches = forward_propagation(minibatch_X, parameters)
# Compute cost and add to the cost total
cost_total += compute_cost(a3, minibatch_Y)
# Backward propagation
grads = backward_propagation(minibatch_X, minibatch_Y, caches)
# Update parameters
if optimizer == "gd":
parameters = update_parameters_with_gd(parameters, grads, learning_rate)
elif optimizer == "momentum":
parameters, v = update_parameters_with_momentum(parameters, grads, v, beta, learning_rate)
elif optimizer == "adam":
t = t + 1 # Adam counter
parameters, v, s, _, _ = update_parameters_with_adam(parameters, grads, v, s,
t, learning_rate, beta1, beta2, epsilon)
cost_avg = cost_total / m
if decay:
learning_rate = decay(learning_rate0, i, decay_rate)
# Print the cost every 1000 epoch
if print_cost and i % 1000 == 0:
print ("Cost after epoch %i: %f" %(i, cost_avg))
if decay:
print("learning rate after epoch %i: %f"%(i, learning_rate))
if print_cost and i % 100 == 0:
costs.append(cost_avg)
# plot the cost
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('epochs (per 100)')
plt.title("Learning rate = " + str(learning_rate))
plt.show()
return parameters7.1每次迭代时衰减

Exercise 7 - update_lr
使用指数权重衰减计算新的学习率。
def update_lr(learning_rate0, epoch_num, decay_rate):
"""
使用指数权重衰减计算更新的学习率。
参数:
learning_rate0——原始学习率。标量
epoch_num——epoch数。整数
decay_rate——衰变率。标量
返回:
learning_rate——更新的学习率。标量
"""
learning_rate = learning_rate0 / (1 + decay_rate * epoch_num)
return learning_ratelearning_rate = 0.5
print("Original learning rate: ", learning_rate)
epoch_num = 2
decay_rate = 1
learning_rate_2 = update_lr(learning_rate, epoch_num, decay_rate)
print("Updated learning rate: ", learning_rate_2)
update_lr_test(update_lr)Original learning rate: 0.5
Updated learning rate: 0.16666666666666666
All tests passed
# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, optimizer = "gd", learning_rate = 0.1, num_epochs=5000, decay=update_lr)
# Predict
predictions = predict(train_X, train_Y, parameters)
# Plot decision boundary
plt.title("Model with Gradient Descent optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)
请注意,如果您将衰减设置为在每次迭代时发生,则学习率会过快变为零——即使您从更高的学习率开始。

当你训练几个epoch时,这不会引起很多麻烦,但当epoch的数量很大时,优化算法会停止更新。解决这个问题的一个常见方法是每隔几步就降低学习率。这被称为固定间隔调度。
7.2固定间隔调度
通过将指数学习率衰减安排在固定的时间间隔(例如1000),可以帮助防止学习率过快地变为零。您可以对时间间隔进行编号,也可以将epoch除以时间间隔,时间间隔是具有恒定学习率的窗口大小。

Exercise 8 - schedule_lr_decay
使用具有固定间隔调度的指数权重衰减来计算新的学习率。

def schedule_lr_decay(learning_rate0, epoch_num, decay_rate, time_interval=1000):
learning_rate = learning_rate0 / (1 + decay_rate * (epoch_num // time_interval))
return learning_ratelearning_rate = 0.5
print("Original learning rate: ", learning_rate)
epoch_num_1 = 10
epoch_num_2 = 100
decay_rate = 0.3
time_interval = 100
learning_rate_1 = schedule_lr_decay(learning_rate, epoch_num_1, decay_rate, time_interval)
learning_rate_2 = schedule_lr_decay(learning_rate, epoch_num_2, decay_rate, time_interval)
print("Updated learning rate after {} epochs: ".format(epoch_num_1), learning_rate_1)
print("Updated learning rate after {} epochs: ".format(epoch_num_2), learning_rate_2)
schedule_lr_decay_test(schedule_lr_decay)Original learning rate: 0.5
Updated learning rate after 10 epochs: 0.5
Updated learning rate after 100 epochs: 0.3846153846153846
All tests passed
7.3对每种优化方法使用学习率衰减
7.3.1Gradient Descent with Learning Rate Decay
# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, optimizer = "gd", learning_rate = 0.1, num_epochs=5000, decay=schedule_lr_decay)
# Predict
predictions = predict(train_X, train_Y, parameters)
# Plot decision boundary
plt.title("Model with Gradient Descent optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)

7.3.2??Gradient Descent with Momentum and Learning Rate Decay
# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, optimizer = "momentum", learning_rate = 0.1, num_epochs=5000, decay=schedule_lr_decay)
# Predict
predictions = predict(train_X, train_Y, parameters)
# Plot decision boundary
plt.title("Model with Gradient Descent with momentum optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)

7.3.3Adam with Learning Rate Decay
# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, optimizer = "adam", learning_rate = 0.01, num_epochs=5000, decay=schedule_lr_decay)
# Predict
predictions = predict(train_X, train_Y, parameters)
# Plot decision boundary
plt.title("Model with Adam optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)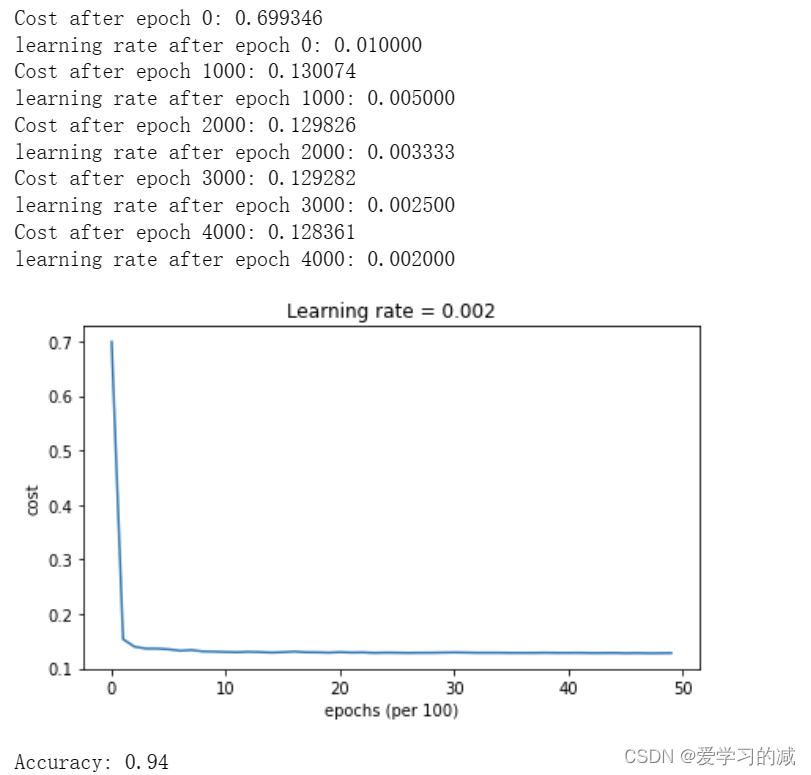

7.4用不同的方法实现相似的性能
使用Mini batch GD或Mini batch-GD With Momentum,精度明显低于Adam,但当在顶部添加学习率衰减时,两者都可以以与Adam相似的速度和精度得分实现性能。
在Adam的情况下,请注意,学习曲线达到了类似的精度,但速度更快。

本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!