基于物理的AlGaN/GaN HEMT器件2DEG电荷密度分析模型(文献阅读)
标题:A Physics-Based Analytical Model for 2DEG Charge Density in AlGaN/GaN HEMT Devices (IEEE TRANSACTIONS ON ELECTRON DEVICES)
重要公式
2DEG电荷密度建模的困难源于量子阱中Ef随ns的复杂变化。此关系由给出
n
s
=
D
V
t
h
[
l
n
(
l
+
e
E
f
?
E
0
V
t
h
)
+
l
n
(
l
+
e
E
f
?
E
1
V
t
h
)
]
(
1
)
n_s=DV_{th}\left[ln\Bigg(l+e^{\frac{E_f-E_0}{V_{th}}}\Bigg)+ln\Bigg(l+e^{\frac{E_f-E_1}{V_{th}}}\Bigg)\Bigg]\right. (1)
ns?=DVth?[ln(l+eVth?Ef??E0??)+ln(l+eVth?Ef??E1??)](1)
其中
E
0
=
γ
0
n
s
2
/
3
E_0=\gamma_0n_s^{2/3}
E0?=γ0?ns2/3?和
E
1
=
γ
1
n
s
2
/
3
\begin{aligned}E_1=\gamma_1n_s^{2/3}\end{aligned}
E1?=γ1?ns2/3??是两个最低子带的能级,Ef 是以伏特表示的费米能级,Vth=kT/q 是热电压。假设AlGaN层完全电离,我们可以写
n
s
=
ε
q
d
(
V
g
o
?
E
f
)
(
2
)
n_s=\frac\varepsilon{qd}(V_{\mathrm{go}}-E_f) (2)
ns?=qdε?(Vgo??Ef?)(2)其中Vgo=Vg?Voff,并且Voff是截止电压。本简式中的计算是针对Al0.15Ga0.85/GaN结构和?3 V的典型Voff进行的。从(1)和(2)可以明显看出,ns相对于Vg的变化是一个复杂的超越函数。
n
s
=
C
g
V
g
o
q
V
g
o
+
V
t
h
[
1
?
ln
?
(
β
V
g
o
n
)
]
?
γ
0
3
(
C
g
V
g
o
q
)
2
/
3
V
g
o
(
1
+
V
t
h
V
g
o
d
)
+
2
γ
0
3
(
C
g
V
g
o
q
)
2
/
3
(
9
)
n_s=\frac{C_gV_\mathrm{go}}q\frac{V_\mathrm{go}+V_\mathrm{th}\left[1-\ln(\beta V_\mathrm{gon})\right]-\frac{\gamma_0}3\left(\frac{C_gV_\mathrm{go}}q\right)^{2/3}}{V_\mathrm{go}\left(1+\frac{V_\mathrm{th}}{V_\mathrm{god}}\right)+\frac{2\gamma_0}3\left(\frac{C_gV_\mathrm{go}}q\right)^{2/3}} (9)
ns?=qCg?Vgo??Vgo?(1+Vgod?Vth??)+32γ0??(qCg?Vgo??)2/3Vgo?+Vth?[1?ln(βVgon?)]?3γ0??(qCg?Vgo??)2/3?(9)
这里,Vgon和Vgod是由插值表达式给出的Vgo的函数
V
g
o
x
=
V
g
o
α
x
V
g
o
2
+
α
x
2
(
10
)
V_\mathrm{gox}=\frac{V_\mathrm{go}\alpha_x}{\sqrt{V_\mathrm{go}^2+\alpha_x^2}}(10)
Vgox?=Vgo2?+αx2??Vgo?αx??(10)
其中 αn = e/β 且 αd = 1/β。我们观察到,(9) 具有正确的极限形式,对应于区域 I 的 (5) 和区域 II 的 (8)。通过在 (2) 中应用 (9),也可以很容易地建立类似的 Ef 统一表达式。
摘要
摘要—在本文中,我们提出了一个基于物理的解析模型,用于描述AlGaN/GaN高电子迁移率晶体管中的二维电子气密度ns。所提出的模型考虑了费米能级Ef和ns之间的相互依赖关系。该模型通过考虑Ef、第一能带E0、第二能带E1以及ns随着栅极电压Vg的变化而进行了建模。所提出的模型与数值计算非常吻合。
关键词—AlGaN/GaN高电子迁移率晶体管(HEMT),解析模型,二维电子气(2DEG)电荷密度。
文章研究了什么
本文研究了 GaN 高电子迁移率晶体管 (HEMT) 器件中二维电子气密度 (2DEG) 对栅压的依赖性。以下是几个重点细节:
- 该研究提出了一种基于物理的完全解析模型,用于描述 GaN HEMT 器件中 2DEG 密度对栅压的依赖性。该模型通过简化不同操作区域的基本器件方程并将其组合起来而开发。
- 所提出的模型没有任何经验参数或拟合参数,并且与广泛温度下的数值计算显示出优异的一致性。
- 该模型可用于开发基于物理的紧凑型 GaN HEMT 器件模型,这有利于器件设计和优化。
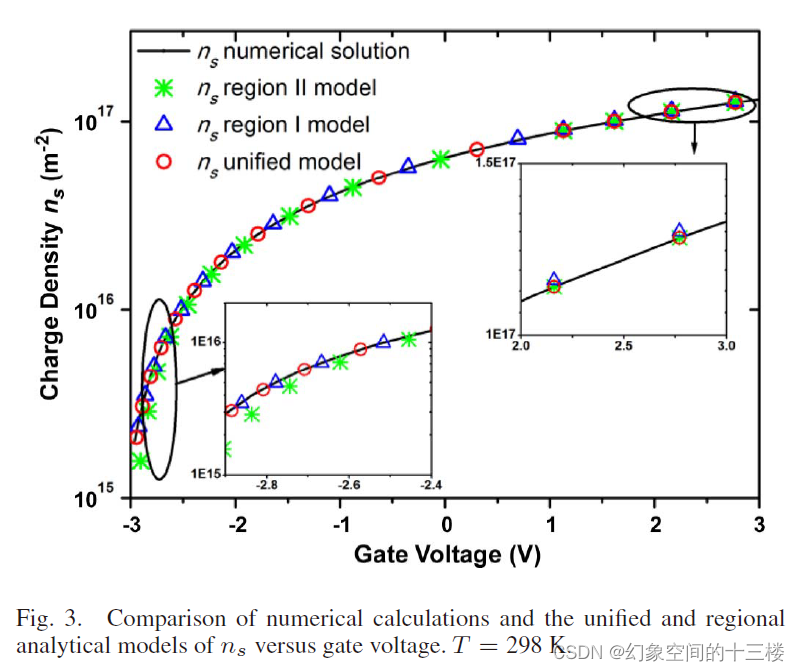
- 将该模型与数值计算进行了比较,结果发现,与区域模型相比,统一模型具有更高的精度,在某些栅极电压范围内,误差通常低于 1%。
- 然而,值得注意的是,假设 EI fVgo 1 不适用于接近截止点的区域,导致该区域的误差增加。
本研究侧重于开发一种解析模型,用于描述 GaN HEMT 器件中 2DEG 密度对栅压的依赖性,并评估其与数值计算的准确性。
文章的创新点
- 本文提出了一种基于物理的完全解析模型,用于描述 GaN HEMT 器件中 2DEG 密度对栅压的依赖性。该模型是通过简化不同操作区域的基本器件方程并将其组合而开发的。
- 所提出的模型没有任何经验参数或拟合参数,使其成为一种更可靠、更准确的器件行为表示。
- 该模型与各种温度下的数值计算显示出极好的一致性,表明其准确性和适用性。
- 该模型可用于开发基于物理的紧凑型 GaN HEMT 器件模型,这有利于器件设计和优化。
- 该研究强调了对 2DEG 密度进行基于物理的解析表达式的必要性,因为目前可用的模型依赖于数值计算、半经验模型或简化近似。
- 所提出的模型为 2DEG 密度提供了一个基于物理的解析表达式,并具有最少的经验参数,为基于 GaN HEMT 器件的电路仿真提供了一种更具洞察力和效率的方法。
本文引入了一种创新的基于物理的解析模型,用于描述 GaN HEMT 器件中 2DEG 密度对栅压的依赖性,与现有模型相比,该模型提供了更高的准确性、可靠性和对器件操作的洞察力。
文章的研究方法
- 文章提出了一种基于物理的完全解析模型,用于描述 GaN HEMT 器件中 2DEG 密度对栅压的依赖性。
- 该模型是通过简化不同操作区域下的基本器件方程并将其组合而开发的。
- 所提出的模型没有任何经验参数或拟合参数。
- 将建模结果与各种温度下的数值计算进行比较,以验证模型的准确性。
- 研究还将所提出的模型与区域模型和统一模型进行了比较,以评估它们的精度和性能。
- 研究方法包括分析器件方程,简化它们,并推导出 2DEG 密度的解析表达式。
- 然后通过与数值计算的比较和与其他模型的性能评估来验证模型。
- 研究方法基于物理分析和数学建模,以开发对器件行为进行全面准确描述的模型。
文章的结论
- 本文提出了一种基于物理的完全解析模型,用于描述GaN HEMT器件中2DEG密度对栅极偏压的依赖性。
- 该模型是通过简化不同操作区域的基本器件方程并将其结合起来开发的,没有任何经验参数或拟合参数。
- 建模结果与各种温度下的数值计算显示出极佳的一致性,表明该模型的准确性和可靠性。
- 该模型可用于开发基于物理的紧凑型GaN HEMT器件模型,这有利于器件设计和优化。
本文提出了一种用于描述GaN HEMT器件中2DEG密度对栅极偏压依赖性的创新型基于物理的解析模型。该模型无需任何经验参数或拟合参数,并且与数值计算结果非常吻合。该模型可用于开发GaN HEMT器件的紧凑型模型,从而辅助器件设计和优化。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!