代码随想录算法训练营 ---第六十天

今天是最后一天，也是最后一题了，单调栈的应用，是昨天单调栈的变形题。

第一题：

简介：

本题和昨天的接雨水题可以说是很相似的一题。我们知道做单调栈问题，我们要先明确我们的单调栈是递增还是递减。由题意知，我们要求最大矩形面积，所以我们需要找左右两边的第一个小的短柱子作为高，所以，我们使用单调递减栈从栈顶到栈底由大到小。面积我们可以看出就是栈顶和栈顶的下一个元素以及要入栈的三个元素组成了我们要求最大面积的高度和宽度。

然后就是分析三种情况

• 情况一：当前遍历的元素heights[i]大于栈顶元素heights[st.top()]的情况
• 情况二：当前遍历的元素heights[i]等于栈顶元素heights[st.top()]的情况
• 情况三：当前遍历的元素heights[i]小于栈顶元素heights[st.top()]的情况

还是建议去跑一遍过程，跑一边过程就明白了，比我在这说好很多。但是要注意几点，本题的特殊点，?我们在目标数组的前后加入了0.

首先来说末尾为什么要加元素0？

如果数组本身就是升序的，例如[2,4,6,8]，那么入栈之后 都是单调递减，一直都没有走 情况三 计算结果的哪一步，所以最后输出的就是0了。 如图：

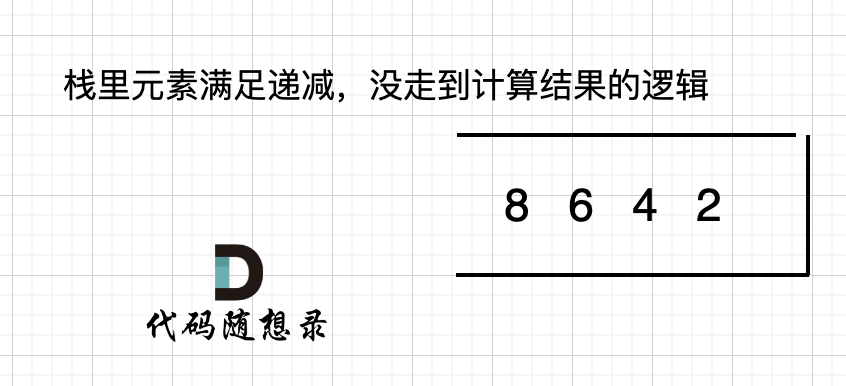
那么结尾加一个0，就会让栈里的所有元素，走到情况三的逻辑。

开头为什么要加元素0？

如果数组本身是降序的，例如 [8,6,4,2]，在 8 入栈后，6 开始与8 进行比较，此时我们得到 mid（8），rigt（6），但是得不到 left。因为 将 8 弹出之后，栈里没有元素了，那么为了避免空栈取值，直接跳过了计算结果的逻辑。之后又将6 加入栈（此时8已经弹出了），然后 就是 4 与 栈口元素 8 进行比较，周而复始，那么计算的最后结果resutl就是0。 如图所示：

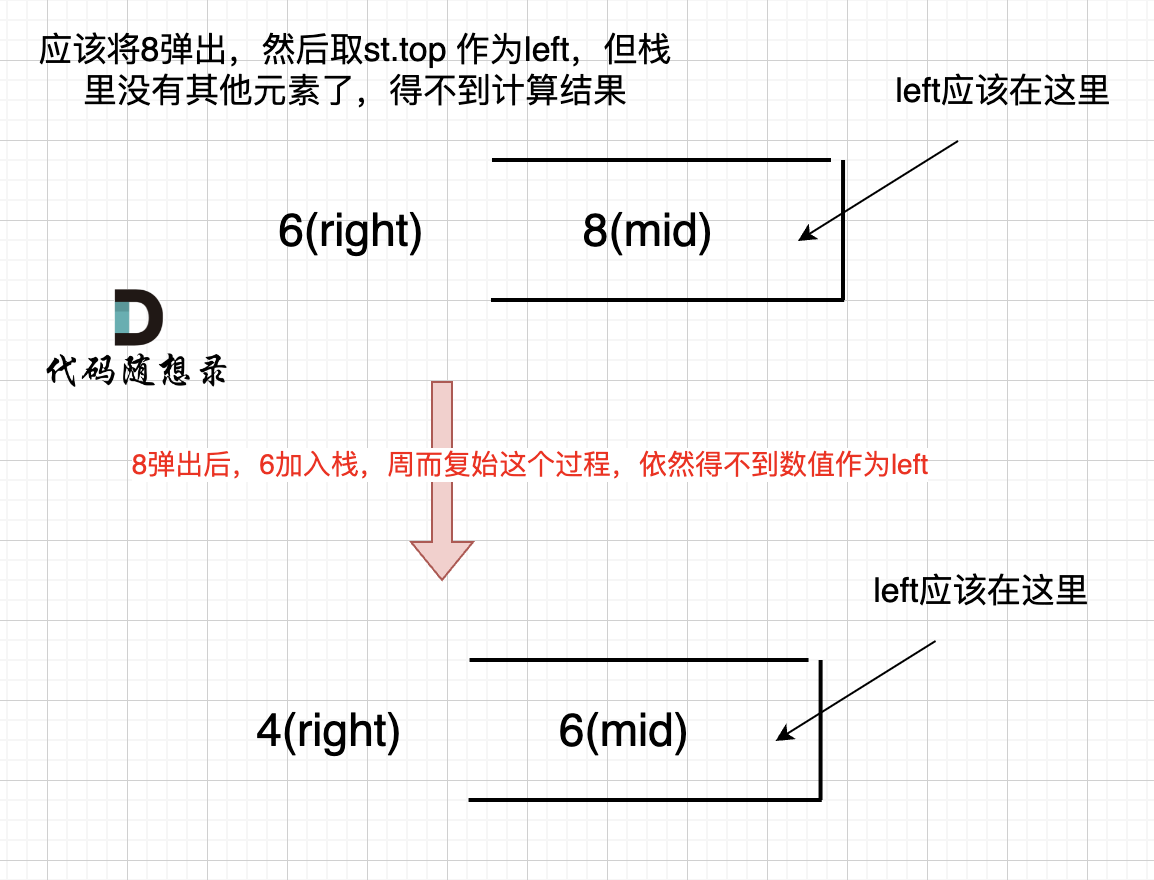
所以我们需要在 height数组前后各加一个元素0。

重要一点：自己跟着程序去DEBUG一遍，很重要。

代码实现：

 int largestRectangleArea(vector<int>& heights) {
        int  result=0;
        stack<int> st;
        heights.insert(heights.begin(), 0); // 数组头部加入元素0
        heights.push_back(0); // 数组尾部加入元素0
        st.push(0);
        for(int i=1;i<heights.size();i++){
            if(heights[i]<heights[st.top()]){
                while (!st.empty() && heights[i] < heights[st.top()]) { // 注意是while
                    int mid = st.top();
                    st.pop();
                    if (!st.empty()) {
                        int left = st.top();
                        int right = i;
                        int w = right - left - 1;
                        int h = heights[mid];
                        result = max(result, w * h);
                    }
                }
                st.push(i);                                 
            }else if(heights[i] == heights[st.top()]){
                st.pop();
                st.push(i);
            }else{
                st.push(i);
            }
        }return result;
    }

总结：?

感觉还不是很得心应手，写的时候总是有地方想不通。还是需要多多练习。