动手学习深度学习学习-循环神经网络

循环神经网络

序列模型

自回归模型

自回归模型（AR模型）和隐变量自回归模型是时间序列分析中的两种重要模型。它们都用于预测和分析时间序列数据，但各有特点和应用场景。

• 定义:自回归模型是一种时间序列模型，它使用先前时间点的观测值来预测未来的值。它基于这样的假设：当前值是之前多个时刻值的线性组合加上一个误差项。
• 数学表示:

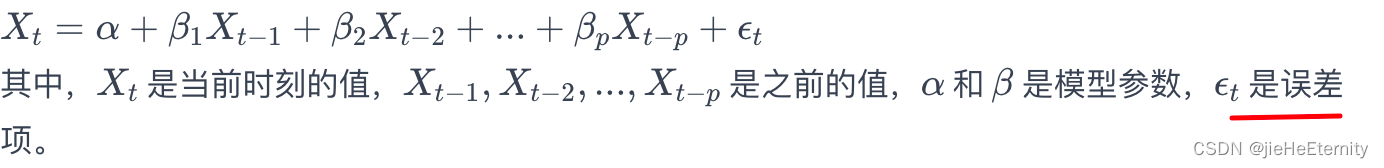
隐变量自回归模型

• 定义
  • 隐变量自回归模型是一种在自回归模型的基础上发展的模型，它在模型中引入了隐变量（latent variables）。这些隐变量可能代表了无法直接观测到的内在因素，它们影响着观测到的时间序列。
• 数学表示

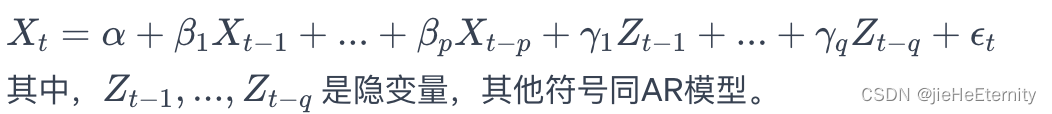
马尔可夫模型

马尔可夫模型是一种统计模型，用于描述一个系统随时间变化的状态，并假设未来的状态只依赖于当前状态，而与之前的历史状态无关。这种特性被称为“无记忆性”或“马尔可夫性质”。马尔可夫模型广泛应用于各种领域，如经济学、物理学、生物信息学、语言处理等。

马尔可夫模型的基本要素:

• 状态集合：系统在任意时刻可能处于的一组不同的状态。
• 转移概率：从一个状态转移到另一个状态的概率。在马尔可夫模型中，这些概率通常用一个转移概率矩阵来表示。
• 初始状态分布：系统在开始时处于各个状态的概率。
  马尔可夫条件:
  马尔可夫条件是马尔可夫模型的一个核心特性，它描述了系统状态转换的“无记忆性”特点。具体来说，马尔可夫条件表明，一个过程中的下一个状态只依赖于当前状态，而与之前的历史状态无关。这个条件简化了对复杂随机过程的建模和分析。
  
  马尔可夫条件的意义:
  

序列模型中的k步预测

在序列模型中的k步预测（或称为k步向前预测）是指使用当前和/或过去的信息来预测序列中未来第k个时间点的值。这种预测方法在时间序列分析和其他序列建模应用中非常常见，尤其是在金融、经济、气象学和各种工程应用中。
k步预测的基本概念
预测步数（k):

• k表示从当前时间点起向前看的步数。例如，如果今天是周一，3步预测意味着预测周四的值。 基于历史数据:
• 使用过去的序列数据（如过去几天的股价、温度等）作为输入。
• 模型的作用:
  依据序列模型（如ARIMA、LSTM等）对未来第k个时间点的值进行估计或预测。

k步预测的应用：

• 金融市场：预测未来几天或几周的股票价格、汇率等。
• 气象学：预测未来几天的天气情况。
• 销售和库存管理：预测产品的未来销量，以便进行库存规划。
• 能源领域：预测未来电力需求，以便进行能源调配和规划。

k步预测的挑战

• 准确性随k值增加而降低：通常，随着预测步数的增加，预测的不确定性和误差可能会增加。
• 模型复杂性：需要选择合适的模型并进行准确的参数调整，以有效捕捉数据中的趋势和季节性变化。
• 对新信息的反应：在实际应用中，模型可能需要定期更新，以包含最新的观测数据，从而提高
• 预测的准确性：在进行k步预测时，理解和处理这些挑战是至关重要的，以确保预测结果的可靠性和有效性。

随着k的增加，k步预测的准确率一般会降低:
，主要有以下的原因。

文本预处理

文本预处理常见步骤包括下面几个步骤：

• 将文本作为字符串加载到内存中。
• 将字符串拆分为词元（如单词和字符）。
• 建立一个词表，将拆分的词元映射到数字索引。
• 将文本转换为数字索引序列，方便模型操作。

词元和词表的定义：
词元（Token）

• 定义：
  词元通常指的是文本中的一个基本单位。在不同的上下文中，一个词元可以是一个词、一个字符、或者更复杂的语言元素（如子词或n-gram）。
• 作用：
  在文本处理中，将文本分割成词元是第一步。这个过程称为词元化（Tokenization），它将原始文本转换为一系列词元，便于后续的处理和分析。
• 示例：
  在英语中，一个句子 “Natural language processing is fun” 可以被词定义：

词表:
词表是一组在特定语料库、数据集或应用中所有唯一词元的集合。换句话说，词表是该语料库中所有独特词元的列表。

• 作用：
  词表在文本处理和模型训练中起到关键作用。它定义了模型可以理解的词汇范围，并用于将词元转换为数值形式（如索引或one-hot编码），这是大多数NLP模型处理文本的基础。
• 示例：
  对于上述句子的词表可能是 [“Natural”, “language”, “processing”, “is”, “fun”, …]，其中包括其他所有独特的词元。元化为 [“Natural”, “language”, “processing”, “is”, “fun”]。

一个例子来介绍词元和词表:
词表是所有唯一词元的集合。

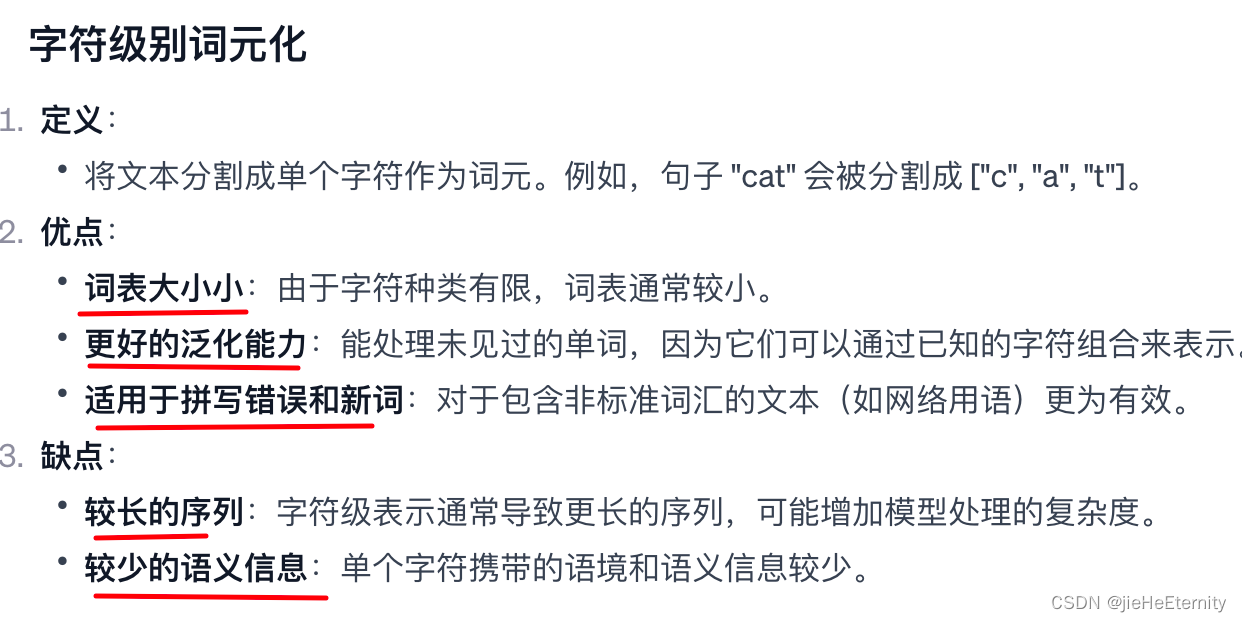
建立单词级别词表和字符级别词表的区别？


总结
字符级别词元化适用于需要高度灵活性和泛化能力的场景，如处理新词、缩写或特殊字符，但它可能捕捉到的语义信息较少。
单词级别词元化则适用于标准语言处理任务，能够有效捕捉单词的丰富语义，但它对未知单词的处理可能是一个挑战。

语言模型和数据集

拉普莱斯平滑
当我们在训练数据中计算某个事件的概率时，如果该事件在训练集中没有出现过，那么按照常规的概率计算方法，这个事件的概率会是0。这在很多应用中是不合理的，因为一个事件在训练集中没有出现，并不意味着它在现实中就完全不可能发生。

引入拉普拉斯平滑的作用就是解决上面的问题:
拉普拉斯平滑（Laplace Smoothing），也被称为加一平滑（Add-One Smoothing），是一种用于处理分类问题中的概率估计的技术，尤其在自然语言处理（NLP）中的文本数据处理领域中应用广泛。它的主要目的是解决数据稀疏问题，即在训练集中没有或很少出现某些项的情况。

基本原理

拉普拉斯平滑通过在所有可能的类别的计数上加一个小的正数（通常是1）来解决这个问题。这样即使对于那些在训练集中没有出现过的事件，也会分配一个小的非零概率。

自然语言处理中读取长序列的两种方式:

随机采样和顺序分区

随机采样
随机采样是一种将长序列随机切分成一系列短序列的方法。在这种采样方式中，每个小批量数据可能包含原始序列中随机位置的子序列。

操作流程:

• 随机选择序列的起始位置。
• 从该位置开始，根据预定的序列长度切分序列，生成一个小批量的训练样本。
• 重复这个过程，直到覆盖整个数据集。

特点:

• 优点: 由于采样是随机的，模型在每次迭代中学习到的是不连续的、独立的序列片段，这有助于模型学习到更泛化的特征。
• 缺点: 随机性可能导致相同的序列片段在一个训练周期中被重复采样，而其他片段可能被忽略。

顺序分区

• 顺序分区是一种顺序地将长序列切分成短序列的方法。这种方法保持了原始序列中的顺序，使得连续的小批量之间存在一定的关联。

操作流程:

• 将整个序列按顺序分成若干个固定长度的子序列。
• 每个子序列作为一个小批量进行处理。
• 小批量之间的顺序和原始序列保持一致。

特点:

• 优点: 保持了序列之间的时间连续性和上下文关系，对于需要理解序列内长距离依赖的模型来说很有帮助。
• 缺点: 模型可能对序列中的特定模式过度适应，影响其泛化能力。

循环神经网络

对隐状态使用循环计算的神经网络称为循环神经网络（RNN）。

循环神经网络的隐状态可以捕获直到当前时间步序列的历史信息。

循环神经网络模型的参数数量不会随着时间步的增加而增加。

我们可以使用循环神经网络创建字符级语言模型。

我们可以使用困惑度来评价语言模型的质量。

• 语言模型的困惑度（Perplexity）是衡量语言模型性能的一个重要指标。它基本上是评估语言模型预测一个文本序列的能力有多好的一个度量。困惑度是对语言模型在处理自然语言处理任务时不确定性的量化，困惑度越低，模型的预测性能越好。
• 困惑度是模型在预测样本中每个词的平均不确定性或惊讶度。一个较低的困惑度表示模型对文本的预测更加精准。
• 直观理解
  • 可以将困惑度理解为模型在每个词上做出选择时的平均分支数量。例如，困惑度为10意味着每次预测下一个词时，模型在平均意义上有10个等概率的选择。

循环神经网络的从零开始实现

读取数据集

%matplotlib inline
import math
import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l

batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)

独热编码

F.one_hot(torch.tensor([0, 2]), len(vocab))

X = torch.arange(10).reshape((2, 5))
F.one_hot(X.T, 28).shape

初始化模型参数

def get_params(vocab_size, num_hiddens, device):
    num_inputs = num_outputs = vocab_size

    def normal(shape):
        return torch.randn(size=shape, device=device) * 0.01

    # 隐藏层参数
    W_xh = normal((num_inputs, num_hiddens))
    W_hh = normal((num_hiddens, num_hiddens))
    b_h = torch.zeros(num_hiddens, device=device)
    # 输出层参数
    W_hq = normal((num_hiddens, num_outputs))
    b_q = torch.zeros(num_outputs, device=device)
    # 附加梯度
    params = [W_xh, W_hh, b_h, W_hq, b_q]
    for param in params:
        param.requires_grad_(True)
    return params

循环神经网络模型

def init_rnn_state(batch_size, num_hiddens, device):
    return (torch.zeros((batch_size, num_hiddens), device=device), )

def rnn(inputs, state, params):
    # inputs的形状：(时间步数量，批量大小，词表大小)
    W_xh, W_hh, b_h, W_hq, b_q = params
    H, = state
    outputs = []
    # X的形状：(批量大小，词表大小)
    for X in inputs:
        H = torch.tanh(torch.mm(X, W_xh) + torch.mm(H, W_hh) + b_h)
        Y = torch.mm(H, W_hq) + b_q
        outputs.append(Y)
    return torch.cat(outputs, dim=0), (H,)

创建一个类来包装这些函数

class RNNModelScratch: #@save
    """从零开始实现的循环神经网络模型"""
    def __init__(self, vocab_size, num_hiddens, device,
                 get_params, init_state, forward_fn):
        self.vocab_size, self.num_hiddens = vocab_size, num_hiddens
        self.params = get_params(vocab_size, num_hiddens, device)
        self.init_state, self.forward_fn = init_state, forward_fn

    def __call__(self, X, state):
        X = F.one_hot(X.T, self.vocab_size).type(torch.float32)
        return self.forward_fn(X, state, self.params)

    def begin_state(self, batch_size, device):
        return self.init_state(batch_size, self.num_hiddens, device)

num_hiddens = 512
net = RNNModelScratch(len(vocab), num_hiddens, d2l.try_gpu(), get_params,
                      init_rnn_state, rnn)
state = net.begin_state(X.shape[0], d2l.try_gpu())
Y, new_state = net(X.to(d2l.try_gpu()), state)
Y.shape, len(new_state), new_state[0].shape

预测

def predict_ch8(prefix, num_preds, net, vocab, device):  #@save
    """在prefix后面生成新字符"""
    state = net.begin_state(batch_size=1, device=device)
    outputs = [vocab[prefix[0]]]
    get_input = lambda: torch.tensor([outputs[-1]], device=device).reshape((1, 1))
    for y in prefix[1:]:  # 预热期
        _, state = net(get_input(), state)
        outputs.append(vocab[y])
    for _ in range(num_preds):  # 预测num_preds步
        y, state = net(get_input(), state)
        outputs.append(int(y.argmax(dim=1).reshape(1)))
    return ''.join([vocab.idx_to_token[i] for i in outputs])

梯度裁剪

def grad_clipping(net, theta):  #@save
    """裁剪梯度"""
    if isinstance(net, nn.Module):
        params = [p for p in net.parameters() if p.requires_grad]
    else:
        params = net.params
    norm = torch.sqrt(sum(torch.sum((p.grad ** 2)) for p in params))
    if norm > theta:
        for param in params:
            param.grad[:] *= theta / norm

训练

#@save
def train_epoch_ch8(net, train_iter, loss, updater, device, use_random_iter):
    """训练网络一个迭代周期（定义见第8章）"""
    state, timer = None, d2l.Timer()
    metric = d2l.Accumulator(2)  # 训练损失之和,词元数量
    for X, Y in train_iter:
        if state is None or use_random_iter:
            # 在第一次迭代或使用随机抽样时初始化state
            state = net.begin_state(batch_size=X.shape[0], device=device)
        else:
            if isinstance(net, nn.Module) and not isinstance(state, tuple):
                # state对于nn.GRU是个张量
                state.detach_()
            else:
                # state对于nn.LSTM或对于我们从零开始实现的模型是个张量
                for s in state:
                    s.detach_()
        y = Y.T.reshape(-1)
        X, y = X.to(device), y.to(device)
        y_hat, state = net(X, state)
        l = loss(y_hat, y.long()).mean()
        if isinstance(updater, torch.optim.Optimizer):
            updater.zero_grad()
            l.backward()
            grad_clipping(net, 1)
            updater.step()
        else:
            l.backward()
            grad_clipping(net, 1)
            # 因为已经调用了mean函数
            updater(batch_size=1)
        metric.add(l * y.numel(), y.numel())
    return math.exp(metric[0] / metric[1]), metric[1] / timer.stop()

循环神经网络模型的训练函数既支持从零开始实现， 也可以使用高级API来实现。

#@save
def train_ch8(net, train_iter, vocab, lr, num_epochs, device,
              use_random_iter=False):
    """训练模型（定义见第8章）"""
    loss = nn.CrossEntropyLoss()
    animator = d2l.Animator(xlabel='epoch', ylabel='perplexity',
                            legend=['train'], xlim=[10, num_epochs])
    # 初始化
    if isinstance(net, nn.Module):
        updater = torch.optim.SGD(net.parameters(), lr)
    else:
        updater = lambda batch_size: d2l.sgd(net.params, lr, batch_size)
    predict = lambda prefix: predict_ch8(prefix, 50, net, vocab, device)
    # 训练和预测
    for epoch in range(num_epochs):
        ppl, speed = train_epoch_ch8(
            net, train_iter, loss, updater, device, use_random_iter)
        if (epoch + 1) % 10 == 0:
            print(predict('time traveller'))
            animator.add(epoch + 1, [ppl])
    print(f'困惑度 {ppl:.1f}, {speed:.1f} 词元/秒 {str(device)}')
    print(predict('time traveller'))
    print(predict('traveller'))

num_epochs, lr = 500, 1
train_ch8(net, train_iter, vocab, lr, num_epochs, d2l.try_gpu())

net = RNNModelScratch(len(vocab), num_hiddens, d2l.try_gpu(), get_params,
                      init_rnn_state, rnn)
train_ch8(net, train_iter, vocab, lr, num_epochs, d2l.try_gpu(),
          use_random_iter=True)

循环神经网络的简洁实现

读取数据集

import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l

batch_size, num_steps = 32, 35
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)

定义模型

num_hiddens = 256
rnn_layer = nn.RNN(len(vocab), num_hiddens)

state = torch.zeros((1, batch_size, num_hiddens))
state.shape

X = torch.rand(size=(num_steps, batch_size, len(vocab)))
Y, state_new = rnn_layer(X, state)
Y.shape, state_new.shape

定义一个RNNModel类，只包含隐藏的循环层，我们还需要创建一个单独的输出层。

#@save
class RNNModel(nn.Module):
    """循环神经网络模型"""
    def __init__(self, rnn_layer, vocab_size, **kwargs):
        super(RNNModel, self).__init__(**kwargs)
        self.rnn = rnn_layer
        self.vocab_size = vocab_size
        self.num_hiddens = self.rnn.hidden_size
        # 如果RNN是双向的（之后将介绍），num_directions应该是2，否则应该是1
        if not self.rnn.bidirectional:
            self.num_directions = 1
            self.linear = nn.Linear(self.num_hiddens, self.vocab_size)
        else:
            self.num_directions = 2
            self.linear = nn.Linear(self.num_hiddens * 2, self.vocab_size)

    def forward(self, inputs, state):
        X = F.one_hot(inputs.T.long(), self.vocab_size)
        X = X.to(torch.float32)
        Y, state = self.rnn(X, state)
        # 全连接层首先将Y的形状改为(时间步数*批量大小,隐藏单元数)
        # 它的输出形状是(时间步数*批量大小,词表大小)。
        output = self.linear(Y.reshape((-1, Y.shape[-1])))
        return output, state

    def begin_state(self, device, batch_size=1):
        if not isinstance(self.rnn, nn.LSTM):
            # nn.GRU以张量作为隐状态
            return  torch.zeros((self.num_directions * self.rnn.num_layers,
                                 batch_size, self.num_hiddens),
                                device=device)
        else:
            # nn.LSTM以元组作为隐状态
            return (torch.zeros((
                self.num_directions * self.rnn.num_layers,
                batch_size, self.num_hiddens), device=device),
                    torch.zeros((
                        self.num_directions * self.rnn.num_layers,
                        batch_size, self.num_hiddens), device=device))

训练与预测

device = d2l.try_gpu()
net = RNNModel(rnn_layer, vocab_size=len(vocab))
net = net.to(device)
d2l.predict_ch8('time traveller', 10, net, vocab, device)

num_epochs, lr = 500, 1
d2l.train_ch8(net, train_iter, vocab, lr, num_epochs, device)

num_epochs, lr = 500, 1
d2l.train_ch8(net, train_iter, vocab, lr, num_epochs, device)

通过时间反向传播

在循环神经网络（RNN）中，梯度更新确实涉及两个方面：一是沿着网络层的反向传播，二是沿着时间维度的逆向反向传播。这两部分共同工作以确保RNN能够学习序列数据中的时序依赖性。让我们详细探讨一下这两部分。