INT201 形式语言与自动机笔记（下）

L6 Context-Free Languages?上下文无关语言

Context-Free Grammar (CFG)

是一组用于生成字符串模式的递归规则。上下文无关的语法可以描述所有的常规语言，但它们不能描述所有可能的语言。

e.g

遵循这些规则，我们可以生成一种语言:

上下文无关文法 Context Free Grammar

上下文无关的语法是一个4元组G = (V， Σ， R, S)，其中

1. V是一个有限集合，它的元素叫做 Variable，
2. Σ是一个有限集合，它的元素称为 Terminal，
3. V∩Σ =?，
4. S是V的一个元素;它被称为start variable，
5. R是一个有限集合，它的元素称为rules。每条rule 的形式是A→w，其中A∈V, w∈(V∪Σ)*

e.g1

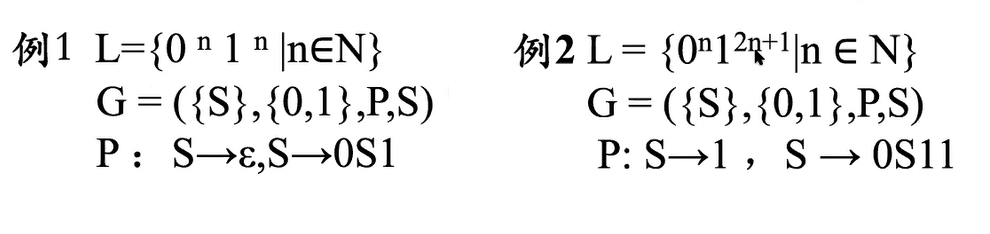
e.g2

e.g3

e.g4

?正则语言属于上下文无关语言

?语法分析树

e.g1

边缘/结果

Derivation派生/推导

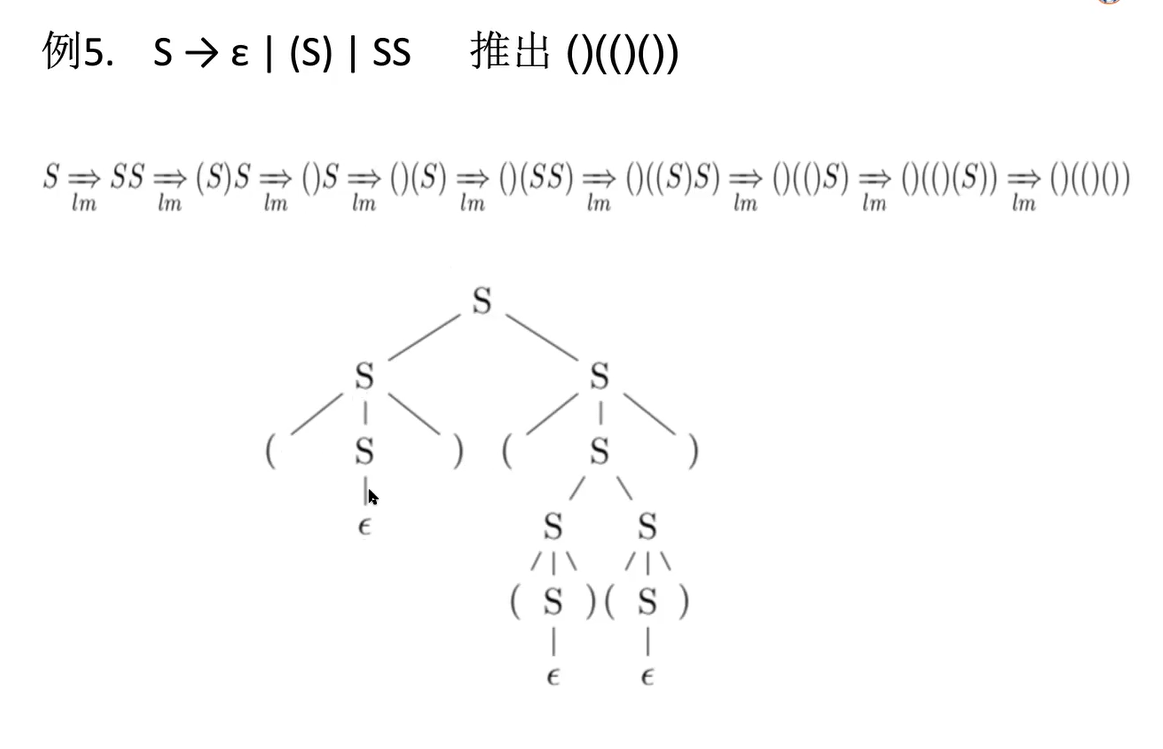
?e.g1

e.g2

e.g3

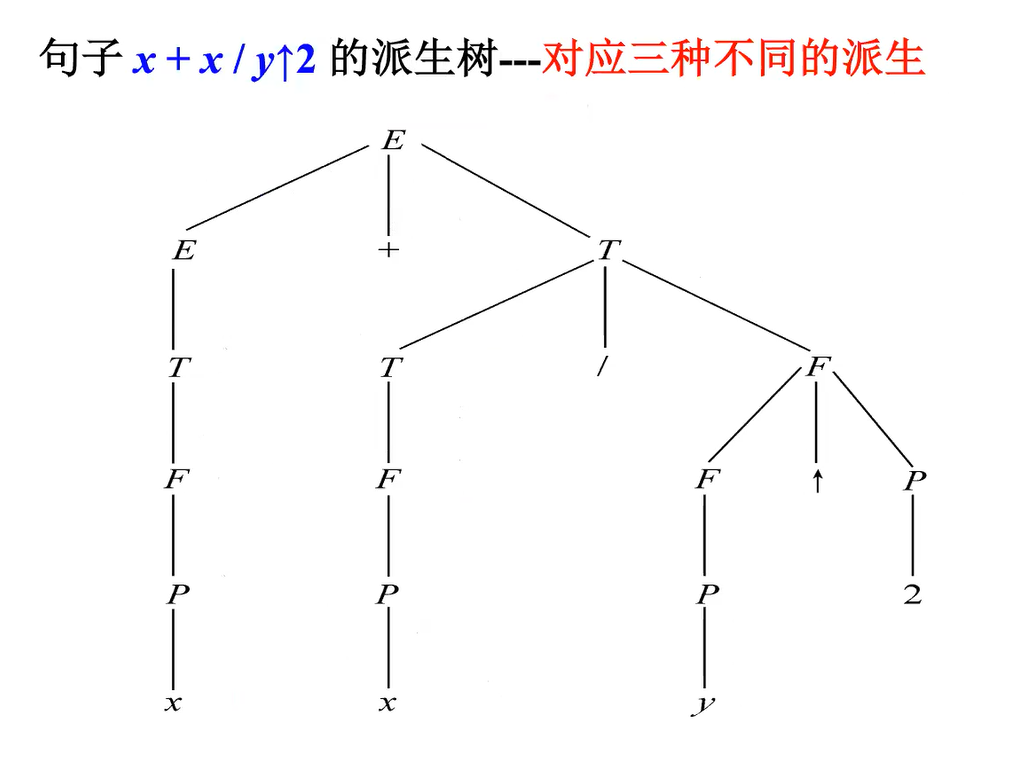
歧义性 ambiguity

e.g1

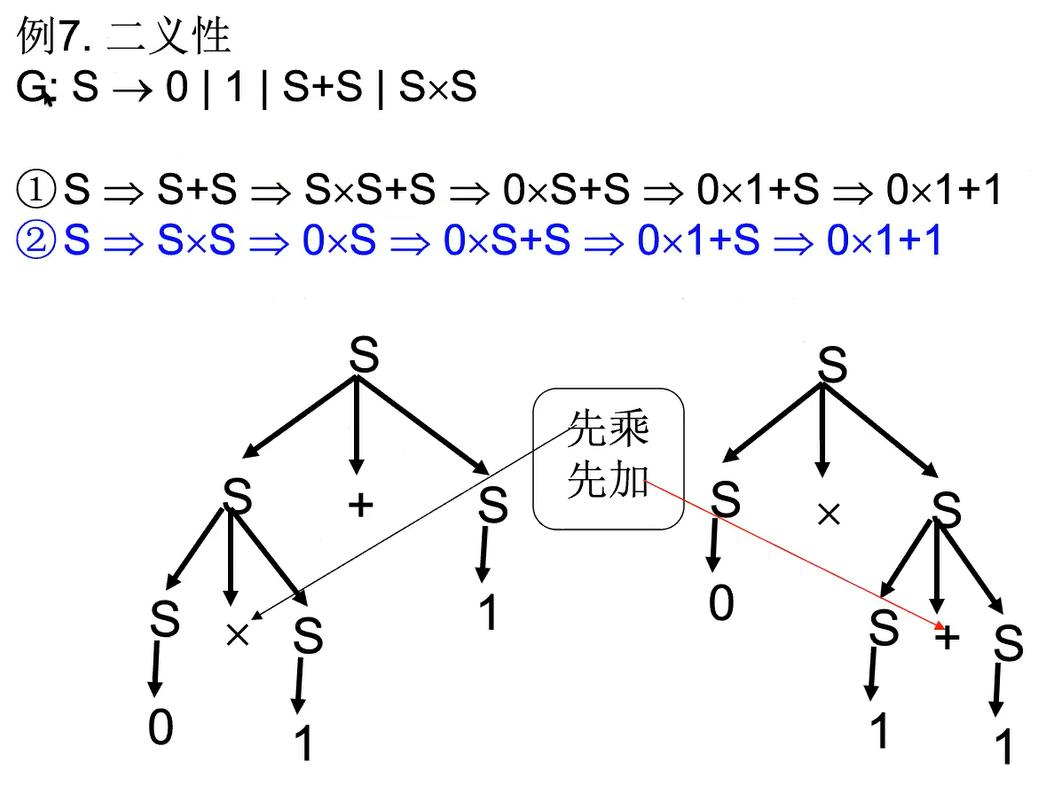
用CFG获取字符串和语言

CFG的语言

定义

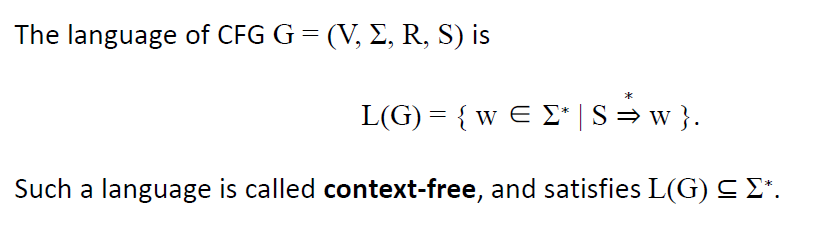
例1（？）

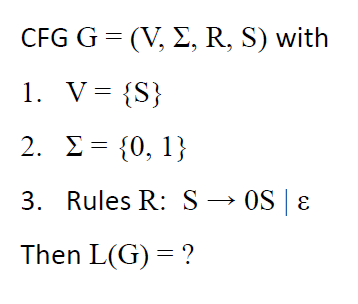
例2（？）

Palindrome 回文

例3

正则语言是上下文无关的

以Σ为字母表，以L≥Σ *为Regular语言。那么L是一种无关上下文的语言(所有Regular语言都是无关上下文的)。

例1（？）

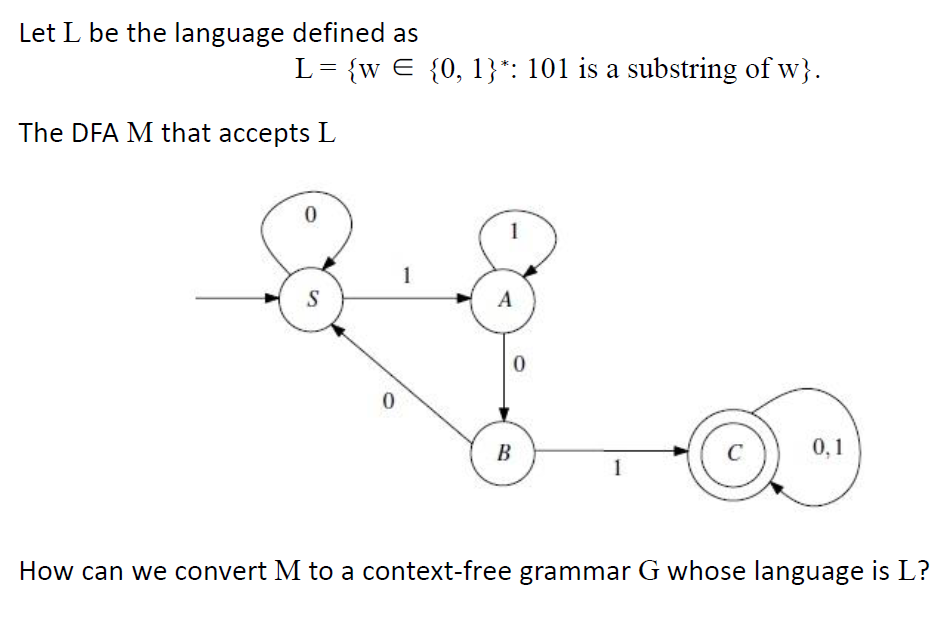
例2（？）

Chomsky Normal Form (CNF) 乔姆斯基范式

定义

每一个上下文无关语法G = (V， Σ， R, S)?都是乔姆斯基范式，如果R中的每个规则都有以下三种形式之一:

?A→BC，其中A、B、C是V的元素，B≠S, C≠S。
?a→x，其中a是V的元素，a是Σ的元素。
?S→ε，其中S为起始变量

原因

更容易使用

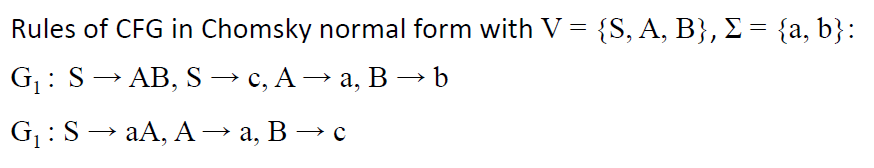
理论

让Σ成为一个字母，让L? Σ *成为一个无上下文的语言。存在一种乔姆斯基范式的上下文无关语法，其语言为L(每个CFL都可以用CNF中的一个CFG来描述)。

证明

给定CFG G = (V， Σ， R, S)，逐一替换所有非“乔姆斯基”规则。

?启动变量(RHS规则不允许)?也就是在规则的末尾，不能再出现开始变量。也就是说，规则的右侧不能再包含起始符号。
?ε-规则(当A不是启动变量时不允许A→ε)
?所有其他违规行为(A→B、A→aBc、A→BCDE)

把CFG转化成CNF

步骤

步骤1。从规则的右侧删除start变量。

步骤2。去掉?ε-rules A→ε，其中A∈V?{S}

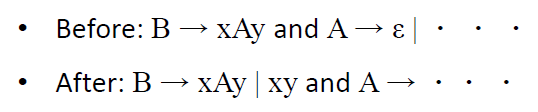
当删除A→ε-rules 时，插入所有新的替换:

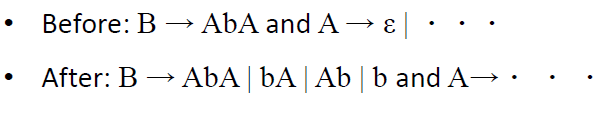
步骤3。移除单位规则A→B，其中A∈V。

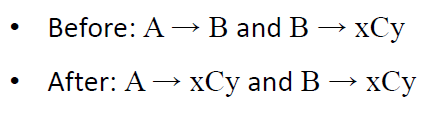
步骤4。消除所有右边有两个以上符号的规则。

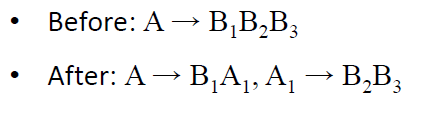
第5步。消除所有形式为A→ab的规则，其中A和b不都是变量。

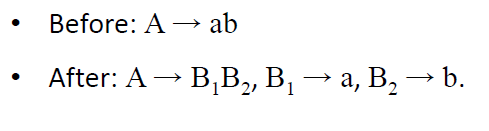
Closure property of CFG

理论1：

如果𝐿1and𝐿2是上下文无关的语言，那么它们的联合𝐿1∪𝐿2也是上下文无关的。

理论2：

如果𝐿1and𝐿2是无关上下文的语言，它们的联合𝐿1°𝐿2也是无关上下文的。（？）

理论3：?

如果𝐿1 is是与上下文无关的语言，它们的Kleene闭包𝐿* 1也是与上下文无关的。（？）

Syntactic parsing 语法解析(optional)

用上下文无关语法解析自然语言

例1

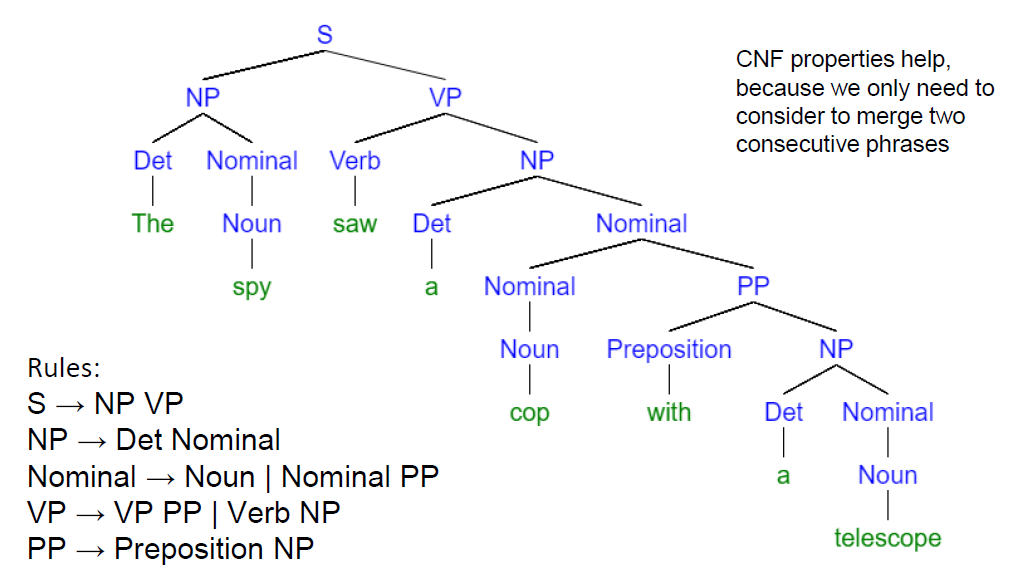
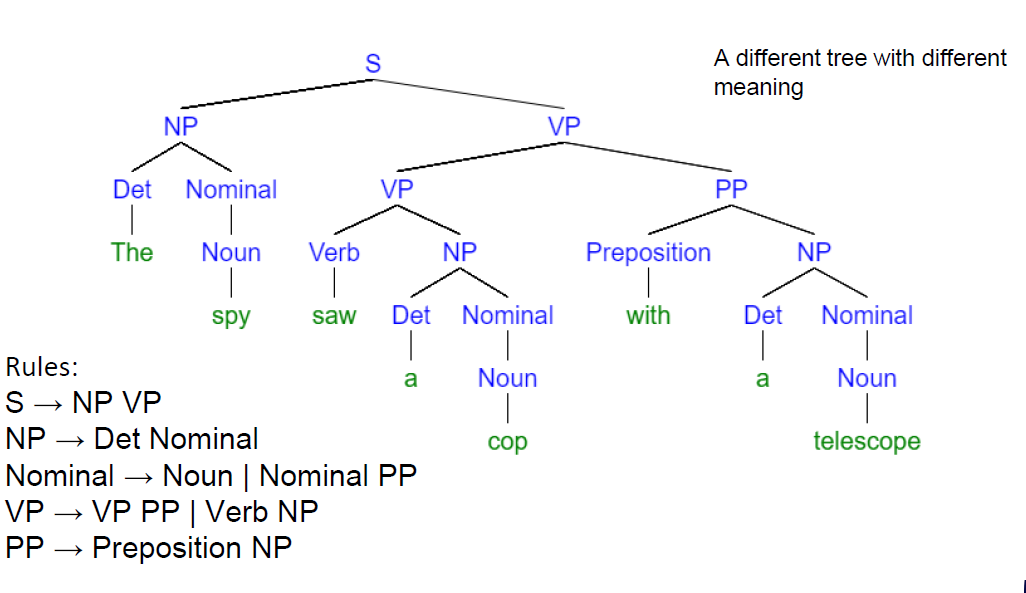
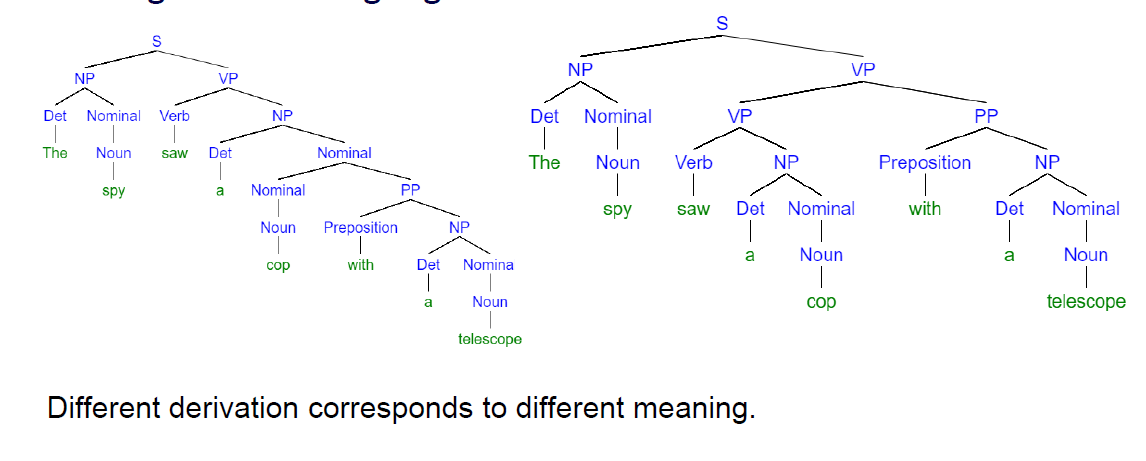
Pushdown Automata下推自动机

下推自动机可以接受的语言类别正是上下文无关的语言类别(有限自动机适用于常规语言)。

成分：tape， stack, state control

tape, tape head, stack, stack head, state control

PDA和NFA唯一的区别就是多了stack

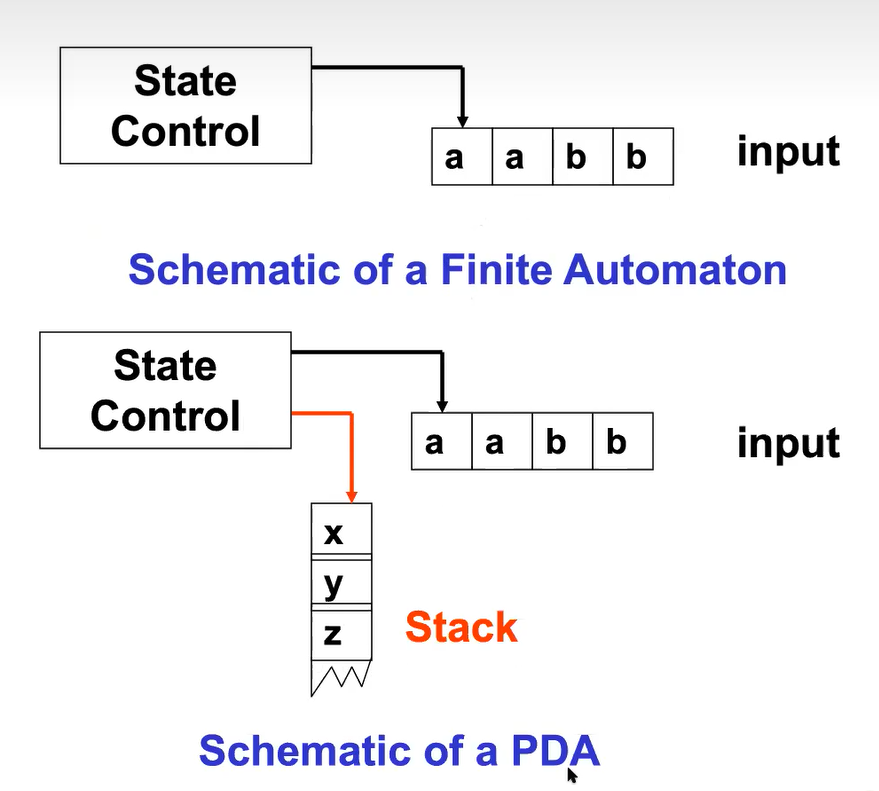
PDA Definition

1.六元组

7元组

e.g1 六元组

?$是压箱底的，平时不用

?e.g2

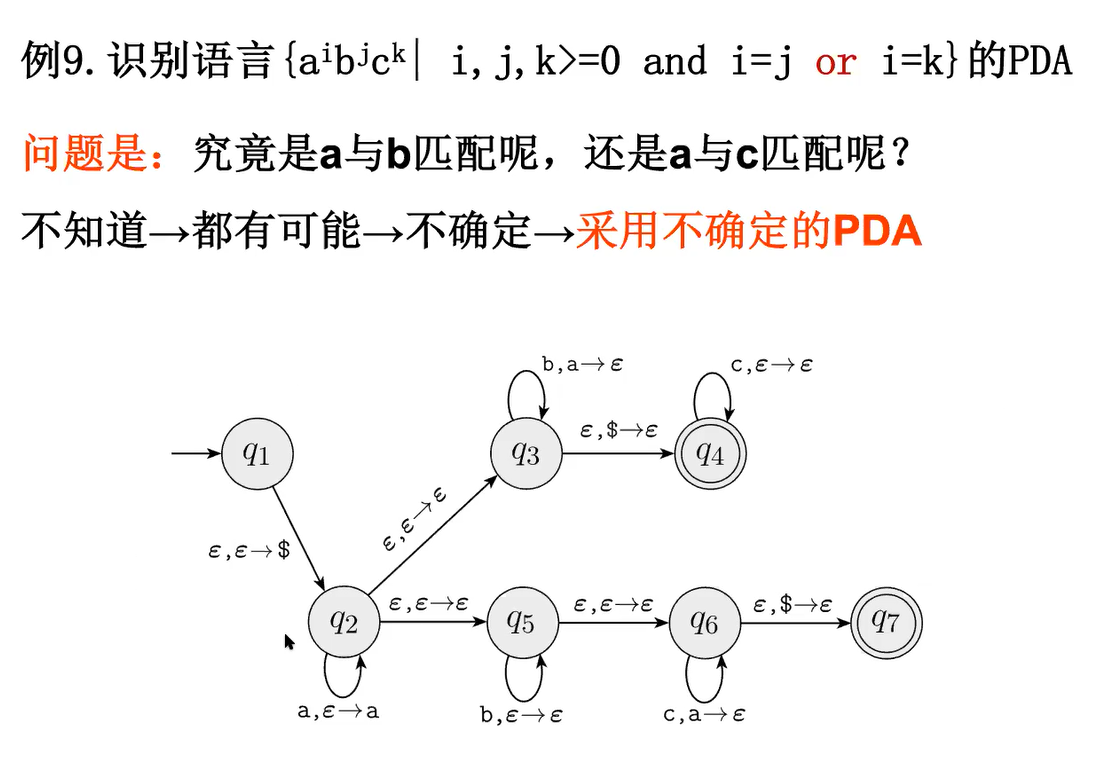
e.g3 7元组

瞬时描述

PDA接受的语言

e.g1

CFL构造PDA

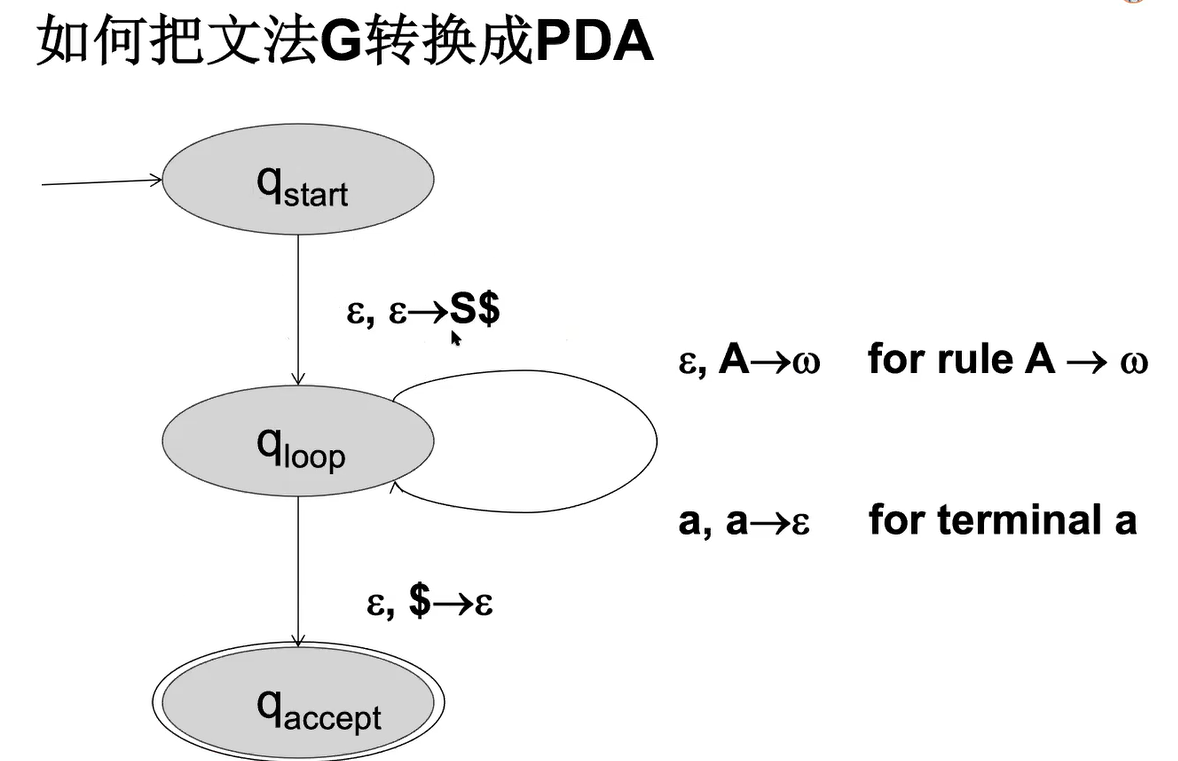
e.g1

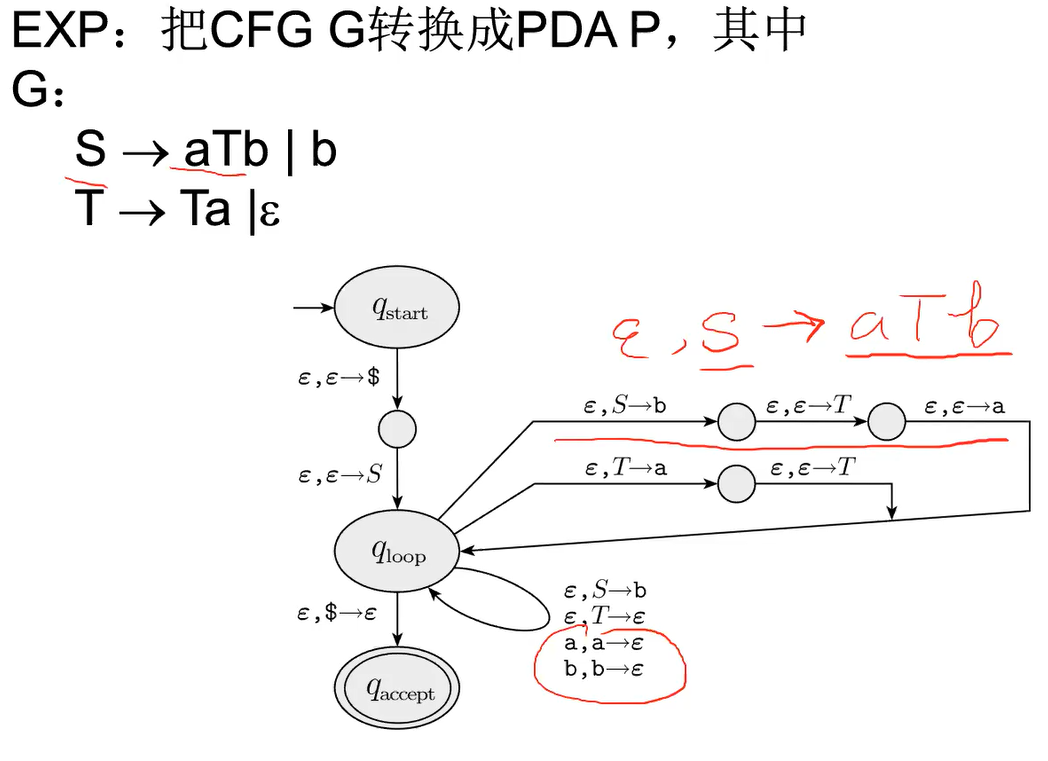
e.g2

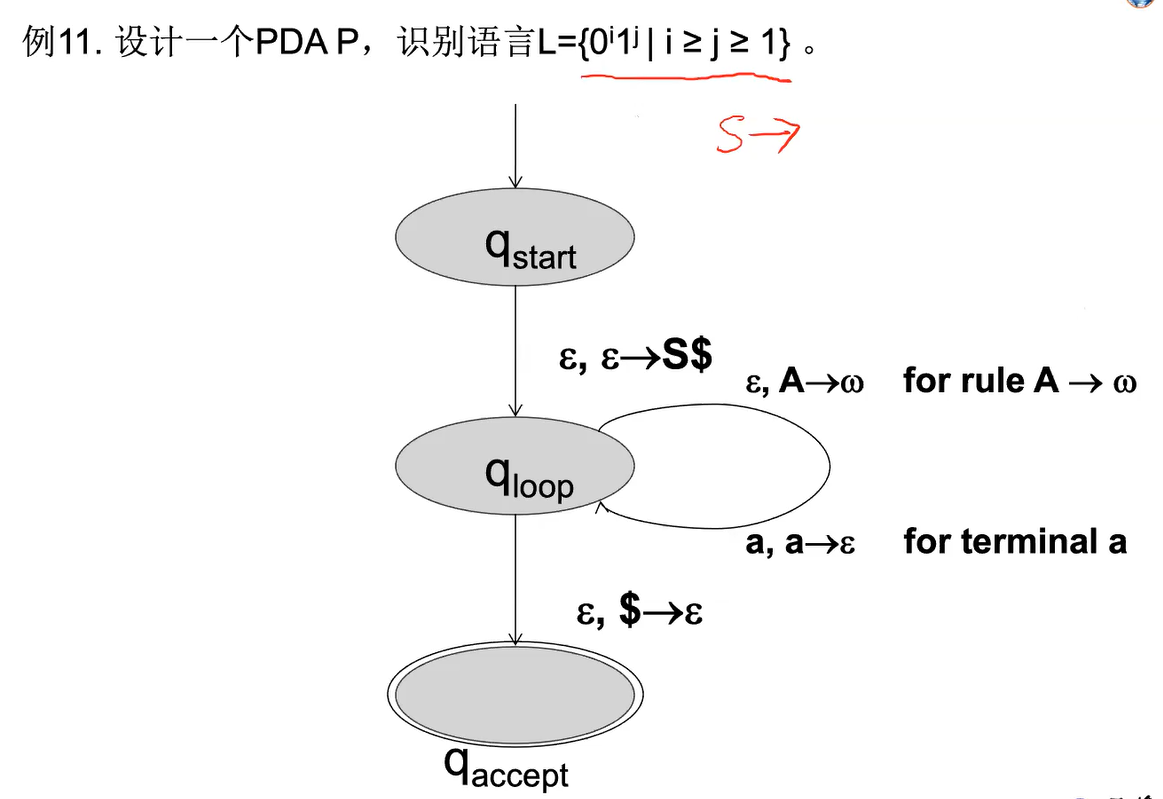
e.g3?

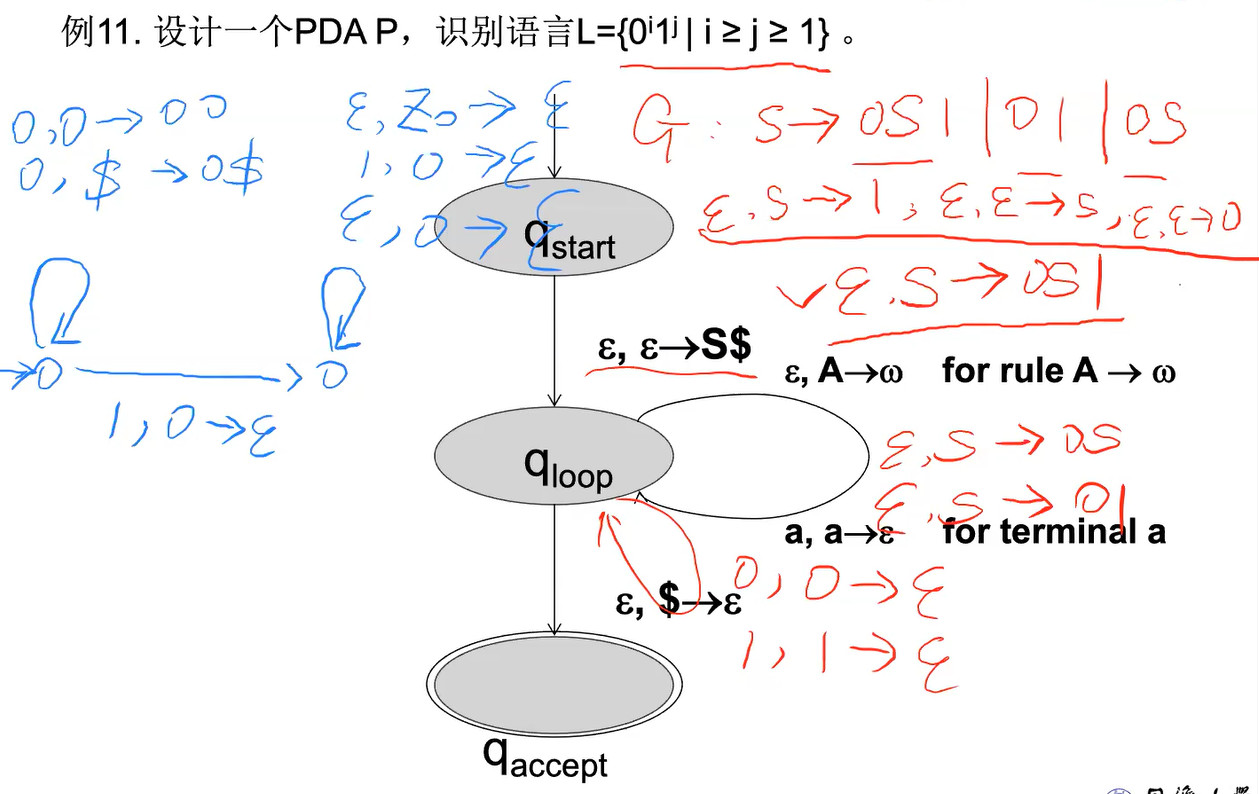
确定性下推自动机?DPDA

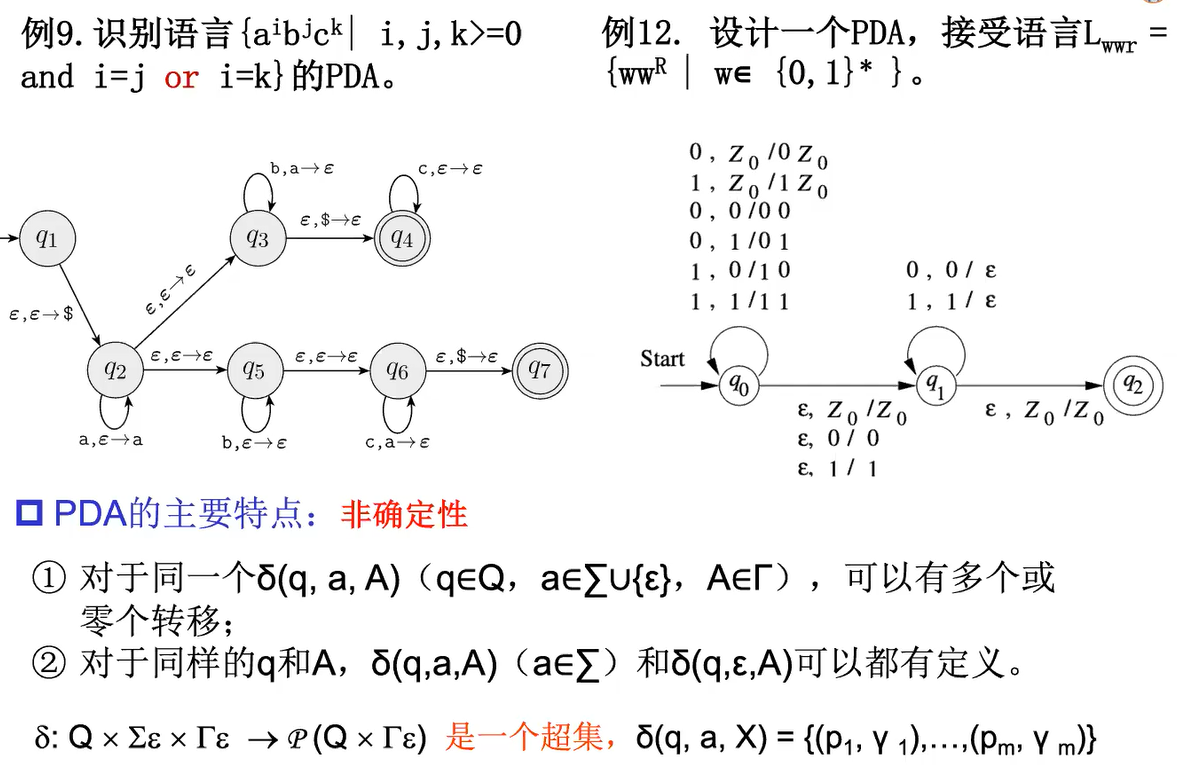
例12中，q0是把前半部分压进去，q1是做前后部分的匹配，q2是可接受状态

e.g1

DPDA能识别RL

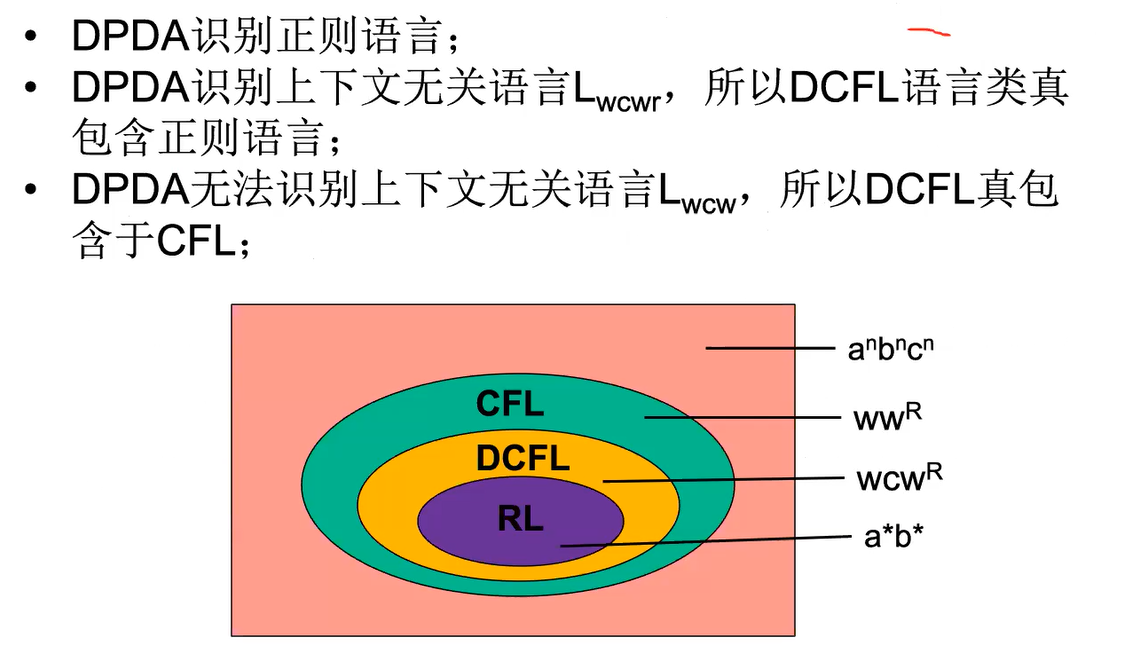
Lec 9 Turing Machine and Variants

Properties of Turing Machine

TM Configuration 格局

TM Transitions

TM Computation

Yields产生

可识别?

?可判定（可计算）

e.g1

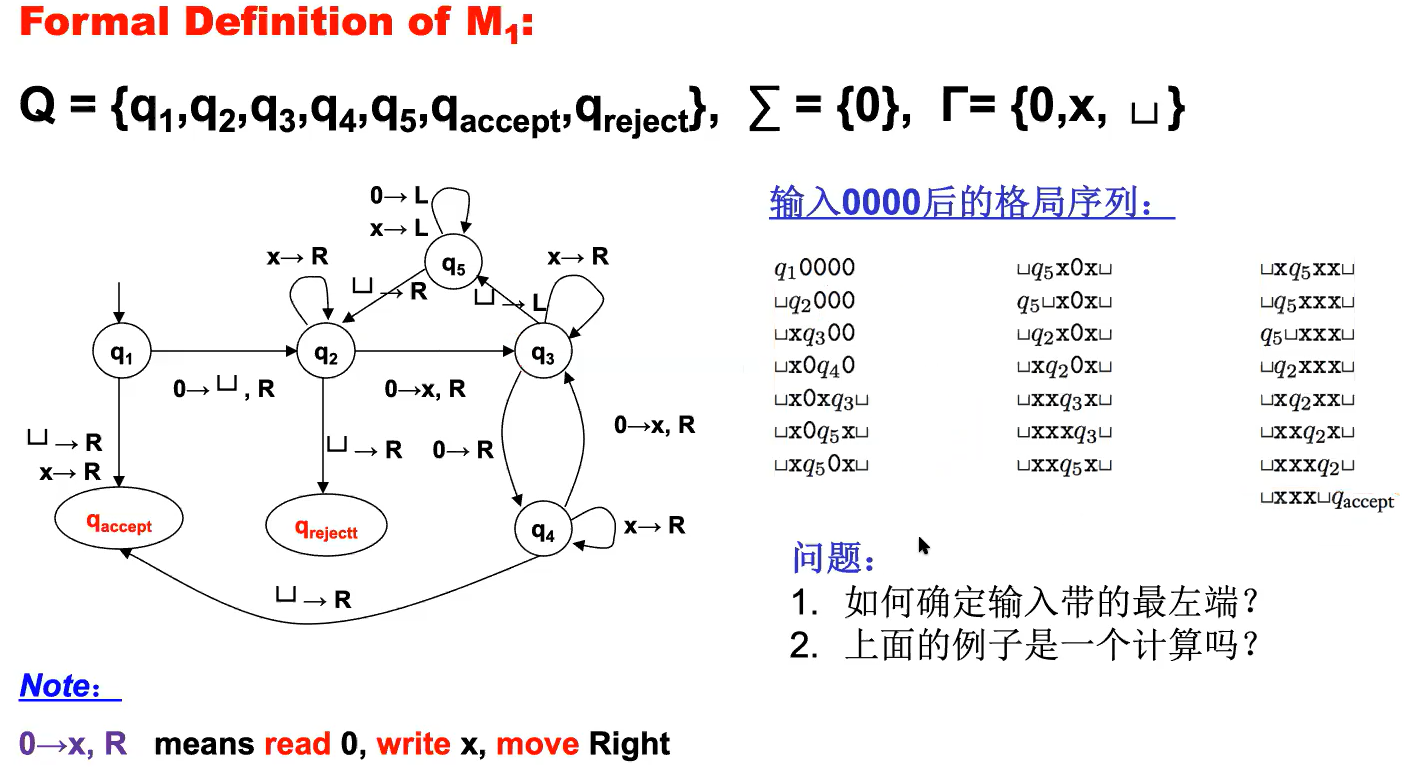
e.g2

Language accepted by TM

Decider

Multi-tape TM 多带图灵机

Multi-tape TM equivalent to 1-tape TM??

单带图灵机和多带实际上是等价的，只是提速和简化了

Nondeterministic TM （NTM）

?e.g1

NTM equivalent to TM

因为等价性，以后尽可能用高级工具，多带NTM

?

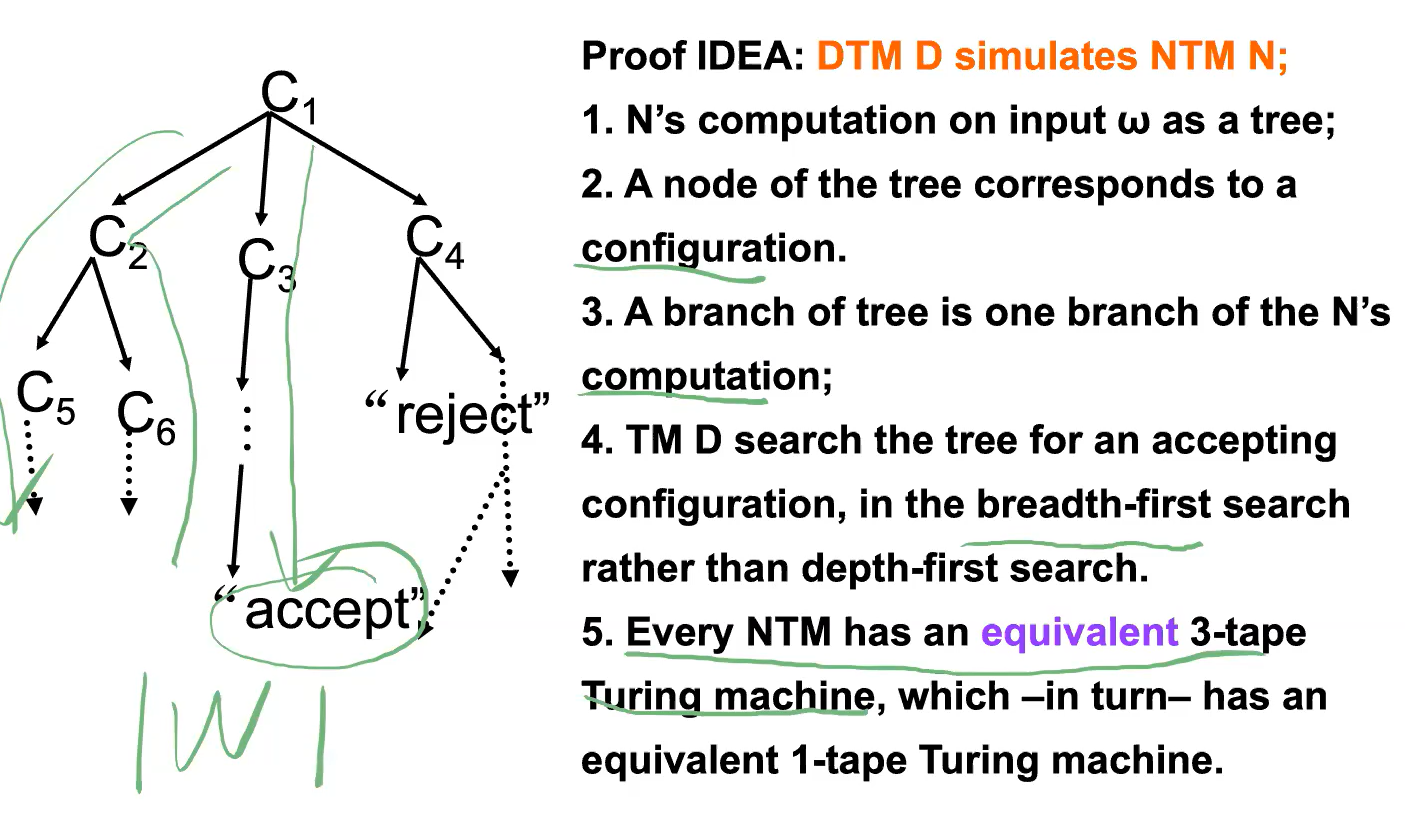
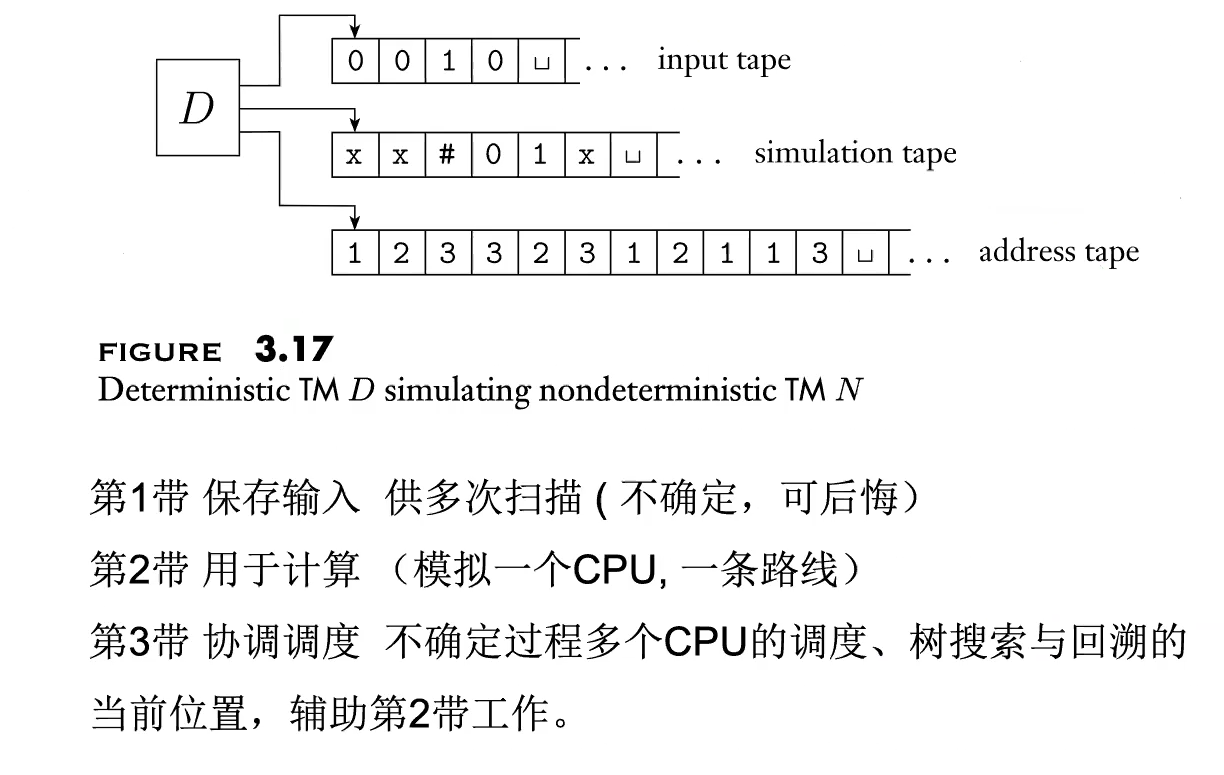
?在有穷的时间内吧所有的分支都走完

Address

Simulating NTM by DTM

Encoding

Encoding of Graph

TM to decide the connectedness of a Graph

Lec 10 Recognizable/Decidable Languages

set

Countable set

Uncountable set?

? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

Cantor’s Diagonalization Method康托的对角化方法

对角线法（zig-zag）? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 补充：区间，实数，无理数都是不可数集? ? ? ? ? ? ? ? ? ? ? ? ? ?

Church-Turing Thesis

任何在算法上可计算的问题同样可由图灵机计算，或者说，每个有效计算都可以由一台图灵机完成

存在不可图灵识别（non Turing-recognizable）的语言

推论1：图灵机的数量是可数的（因为这些二进制数字和特殊符号是可数的）

命题2：语言的数量是不可数的

由此，我们再次得出一个推论：图灵不可识别的语言是存在的

Decidability 可判定性

Acceptance problem for computation model

Acceptance problem for Language LDFA

Acceptance problem for Language LNFA

Acceptance problem for Language LCFG

一个空的CFG是可判定的

The Language LTM is Turing-recognizable

The Language LTM is undecidable

我们不知道通用图灵机是否会停止工作。与我们之前看到的所有机器不同，TM可能永远运行下去。

Instance of non Turing-recognizable languages?关于非图灵识别语言的实例

Universal Turing Machine 通用图灵机

存在一个TM U，它接受一个图灵机描述和输入磁带，并在输入磁带上模拟给定图灵机的一个步骤。（如下图）其中：TM U的输入格式为：<M,w>，其中M是对指定TM的描述，w是(转换后)的输入。

Examples of decidable languages

对问题的相关语言无法被一个图灵机识别，因为该图灵机无法对该语言所有输入都能做到停机判断（存在输入导致图灵机无法停机）

Existence of undecidable language and non-Turing recognizable language

不可识别问题：问题的相关语言不能被TM识别?其中注意：一个不可判定语言是可以被识别的

Lec 11?Reducibility and Undecidable Languages

Ruducibility 规约性

Mapping Reduction

The Halting Problem and other undecidable languages

Halting problem for TMs is undecidable

Emptiness of TMs is undecidable

Rice’s Theorem

Non-trivial Properties

Rice’s Theorem

Applications

Non-Applications