MIT18.06线性代数笔记2

2023-12-13 05:02:01

文章目录

正交向量与子空间

向量正交：x^Ty=0
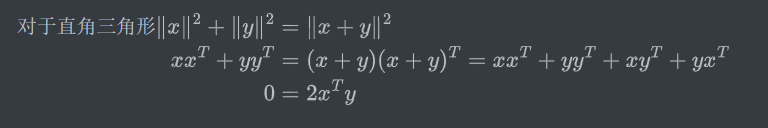
在这里插入图片描述

空间正交：S中每个向量与T中每个向量正交

行空间正交于零空间，同理列空间正交于左零空间
在这里插入图片描述

在实际应用中，数据可能会有干扰项，此时会导致Ax=b无解，使用A^TAx=A^Tb得到最优解，去除干扰

A^TA不一定可逆，如果要可逆则A的列线性无关

子空间投影

在二维空间中，p是b在a上最接近a的向量（投影）：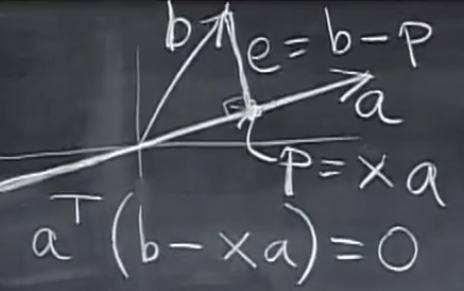

化简得
$\begin{aligned} a^Tb &= xa^Ta\\ x &= \frac{a^Tb}{a^Ta}\\ 代入得 &p=a\frac{a^Tb}{a^Ta} \end{aligned}$
b翻倍p也翻倍，a翻倍p不变

投影是由矩阵完成的（投影矩阵）：
$p=Pb\\ 根据p=a\frac{a^Tb}{a^Ta}得：P=\frac{aa^T}{a^Ta}$
a^Ta是数字，aa^T是列向量乘行向量

这个矩阵的列空间C§=a所在的直线，因为这个矩阵乘b变成了b在a直线的投影

rank§=1，因为P由列乘行产生，这一个列是列空间的基

P是对称矩阵，转置是它自己

P²=P，再投影一次不变

为什么做投影：因为Ax=b可能无解，此时只能求解最接近的那个可解问题Ax=p，p即是b在列空间的投影

在三维空间中：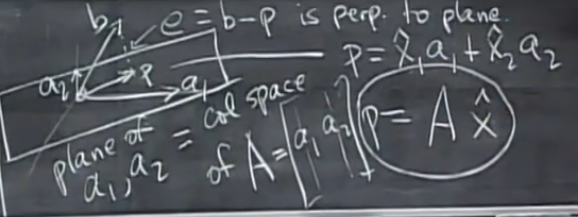

空间中平面由a1，a2两基向量产生，A=[a1 a2]，b在平面上的投影为p，需要求出x使得Ax=p

e=b-Ax，e垂直于平面（也就垂直于a1和a2）
$a_1^T(b-Ax)=0 \\ a_2^T(b-Ax)=0 \\ 整理成矩阵： A^Te= \begin{bmatrix} a_1^T\\ a_2^T \end{bmatrix} (b-Ax)= \begin{bmatrix} 0\\ 0 \end{bmatrix}$
e位于A的转置的零空间，因为左零空间正交于列空间，所以e垂直于A的列空间

$\begin{aligned} A^TAx &= A^Tb\\ x &= (A^TA)^{-1}A^Tb\\ 代入得p &= Ax=A(A^TA)^{-1}A^Tb \end{aligned}$
这里的A(A^TA)^-1A^T相当于投影到一维空间时的aa^T/a^Ta，就是投影矩阵P
$当A为可逆方阵时，P=A(A^TA)^{-1}A^T=AA^{-1}(A^T)^{-1}A^T=I\\ 因为A为n\times n可逆方阵时，列空间为整个n维空间，把n维空间中的b投影到整个n维空间，投影矩阵为单位矩阵$
投影矩阵的特性：

P^T=P
P²=P：P²=A(A^TA)^-1**(A^TA)(A^TA)^-1**A^T=A(A^TA)^-1A^T=P

应用：通过最小二乘法拟合一条直线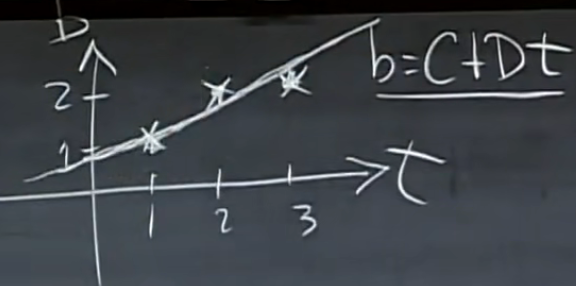

At=b无解，但是A^TAt=A^Tb有解

投影矩阵和最小二乘

b一般会和平面有夹角，此时有垂直于平面和平行于平面的两个分量，平行的分量就是投影，投影矩阵就是把垂直的分量去除

若b在A的列空间里，Pb=b，即b在平面上

若b正交于A的列空间，Pb=0，即b垂直于平面

e也是一个投影，投影矩阵是(I-P)，投影到了与P投影的空间相互正交的空间（这里是左零空间）

最小二乘：找拥有最小的各个误差的平方和的解
$\|e\|^2=\|Ax-b\|^2\\ 最小二乘：使e^2_1+e^2_2+e^2_3最小的解$

$x=(A^TA)^{-1}A^Tb$

线性回归分析：用误差的平方和作为测量总误差的标准

最小二乘法容易受到离群值的影响

无标题

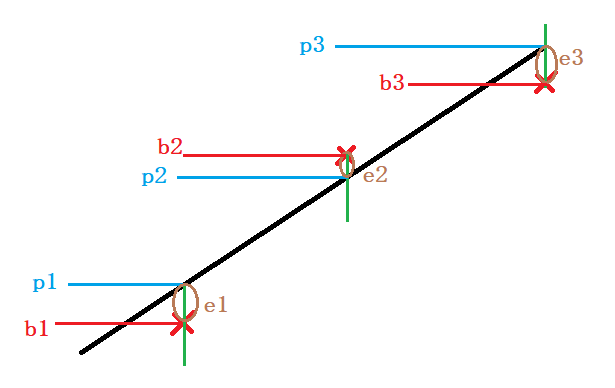
p+e=b

若矩阵A各列线性无关，则A^TA可逆

证明：
在这里插入图片描述

互相垂直的各列一定线性无关（除零向量），这些互相垂直的列向量组成的向量组是标准正交的（标准正交向量组）

正交矩阵和Gram-Schmidt正交化

标准正交向量组中，向量相互正交，即转置相乘为0（内积），但与自身不正交，所以转置相乘为1：

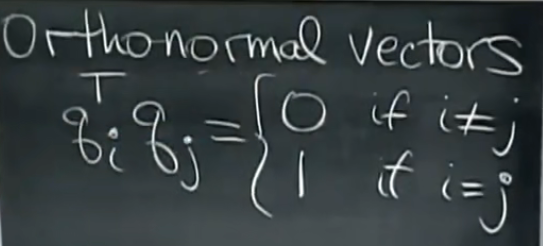
标准正交向量组组成的矩阵（标准正交矩阵）：Q^TQ=I

当标准正交矩阵是方阵的时候（有逆矩阵）称为正交矩阵
$Q^TQ=I\\ Q^T=Q^{-1}$
当有一个方阵时，列互相正交、列向量的长度为1，那么就是正交矩阵：阿德玛矩阵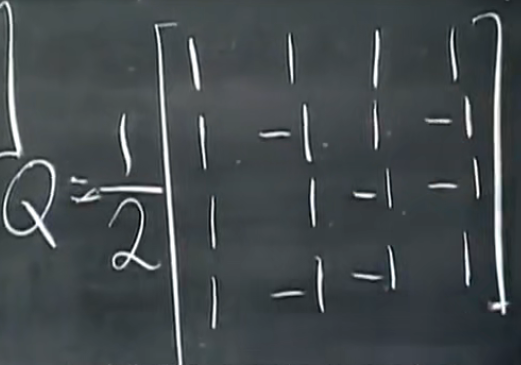

当投影到Q的列空间中：
$P=Q(Q^TQ)^{-1}Q^T=QQ^T\\ 当Q是方阵时，P=QQ^T=I$
而对于拟合过程：
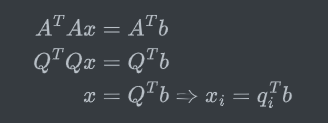
在这里插入图片描述

即已知标准正交基，则在第i个基方向上的投影就等于q_i^Tb

格拉姆-施密特正交化：

从两个线性无关向量开始，取一个向量相对另一向量的垂直分量（e部分），获得一对相互正交的向量A和B，然后向量除长度从而标准化

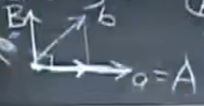
$B=b-p=b-\frac{A^Tb}{A^TA}A\\ 投影p=a\frac{a^Tb}{a^Ta}$
证明：A⊥B
$A^TB=A^T(b-\frac{A^Tb}{A^TA}A)=0$
如果再有c要正交化：
$C=c-p_{c在A上的投影}-p_{c在B上的投影}=c-\frac{A^Tc}{A^TA}A-\frac{B^Tc}{B^TB}B$

正交化后得到的向量组成的空间一样和原来线性无关的向量组成的列空间一样，但是正交化标准化后的Q=[q₁ q₂]比原来的[a b]要好

消元法矩阵表达式：A=LU

格拉姆-施密特法的矩阵表达式：
$\begin{aligned} A&=QR\\ \begin{bmatrix} a & b \end{bmatrix} &= \begin{bmatrix} q_1 & q_2 \end{bmatrix} \begin{bmatrix} a^Tq_1 & b^Tq_1\\ a^Tq_2 & b^Tq_2 \end{bmatrix}\\ &(a^Tq_2=0) \end{aligned}$
由于q₁^Tq₂ = 0，q₁只是a的单位化，所以a^T与q₂也正交，a^Tq₂ = 0

R是一个上三角矩阵

行列式及其性质

行列式的三个性质：

单位矩阵的行列式值为1
交换行，行列式的值符号取反
线性组合
1. 数乘行列式等于数乘一行
2. 两行列式有相同行和不同行，加和等于一个相同行不变、不同行对应元素相加的行列式
两行相等，行列式为0
一行乘以一个数加到另一行，行列式值不变
有零行，则行列式为零
三角阵的行列式值为对角线上元素乘积
A是奇异矩阵（消元后得到零行），A的行列式为0
两矩阵相乘的行列式等于两矩阵的行列式相乘
A^T的行列式等于A的行列式

通过1和2可知，det置换矩阵=1或-1

行列式是一个线性函数

A可逆时行列式不为零，从而消元获得上三角阵U，进而获得对角阵D，值为d₁d₂…d_n
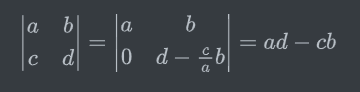
在这里插入图片描述

求A^-1的行列式：
$\begin{aligned} detAA^{-1} &= (detA)(detA^{-1})\\ detA^{-1} &= \frac{1}{detA} \end{aligned}$
通过9和10可知，如果行列式存在零列，行列式同样为零，3和10可知，列交换符号也变化

证明10：
$\begin{aligned} \left|\begin{array}{c} A^T \end{array}\right|&= \left|\begin{array}{c} A \end{array}\right|\\ \left|\begin{array}{c} U^TL^T \end{array}\right|&= \left|\begin{array}{c} LU \end{array}\right|\\ \left|\begin{array}{c} U^T \end{array}\right| \left|\begin{array}{c} L^T \end{array}\right|&= \left|\begin{array}{c} L \end{array}\right| \left|\begin{array}{c} U \end{array}\right|&\text{L是下三角矩阵，U是上三角矩阵，转置后值不变} \end{aligned}$

行交换一次符号取反，置换就可以区分奇偶性

行列式公式和代数余子式

n阶行列式=每行每列都只有一个元素的所有行列式加和（通过3.2分出nⁿ个行列式然后去掉0得到）

行列式公式：
$detA=\sum_{n!个}\pm a_{1\alpha}a_{2\beta}a_{3\chi}\dots a_{n\omega}\\ (\alpha,\beta,\dots,\omega)=(1,2,\dots,n)的一种组合$
n!：从第一行开始，第一行有n个选择，选定后，第二行只有n-1个选择，以此类推

代数余子式：
$以3\times3为例\\ det=a_{11}(a_{22}a_{33}-a_{23}a_{32})+a_{12}(\dots)+a_{13}(\dots)\\ 括号内的就是对应元素a_{1i}的代数余子式\\ a_{11}(a_{22}a_{33}-a_{23}a_{32})= \left|\begin{array}{c} a_{11} & 0 & 0\\ 0 & a_{22} & a_{23}\\ 0 & a_{32} & a_{33} \end{array}\right|= a_{11}\left|\begin{array}{c} a_{22} & a_{23}\\ a_{32} & a_{33} \end{array}\right|\\ a_{12}(-a_{21}a_{33}+a_{23}a_{31})= \left|\begin{array}{c} 0 & a_{12} & 0\\ a_{21} & 0 & a_{23}\\ a_{31} & 0 & a_{33} \end{array}\right|= a_{12}(-\left|\begin{array}{c} a_{21} & a_{23}\\ a_{31} & a_{33} \end{array}\right|)$
代数余子式C_ij符号：当i+j为偶数时取正，为奇数时取负
$detA=a_{11}C_{11}+a_{12}C_{12}+\dots+a_{1n}C_{1n}$
有了代数余子式，我们可以把行列式展开成n-1阶，然后再展开成n-2阶…直到一阶

克拉默法则、逆矩阵、体积

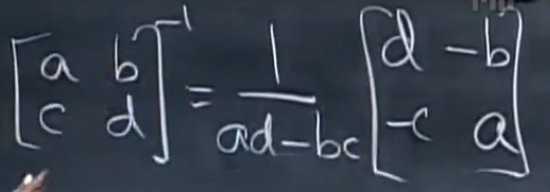
$A^{-1}=\frac{1}{detA}C^T$
证明：
$\begin{aligned} AC^T &= (detA)I\\ \begin{bmatrix} a_{11} & \dots & a_{1n}\\ \dots & \dots & \dots\\ a_{n1} & \dots & a_{nn} \end{bmatrix} \begin{bmatrix} C_{11} & \dots & C_{n1}\\ \dots & \dots & \dots\\ C_{1n} & \dots & C_{nn} \end{bmatrix}&= \begin{bmatrix} ^{\text{第一行元素乘对应代数余子式之和}}detA & \dots & 0\\ \dots & detA & \dots\\ ^{\text{第i行元素乘非第i行对应的代数余子式之和}}0 & \dots & detA \end{bmatrix} \end{aligned}$
克莱姆法则：
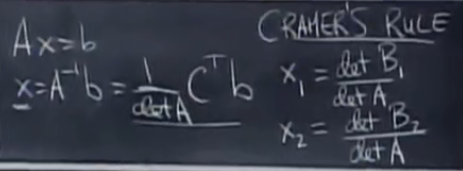
$x=\begin{bmatrix} x_1\\ x_2\\ \dots \end{bmatrix}$

$B_1=\begin{bmatrix} b_1 & a_{12} & \dots & a_{1n}\\ b_2 & a_{22} & \dots & a_{2n}\\ \dots & \dots & \dots & \dots\\ b_n & a_{n2} & \dots & a_{nn} \end{bmatrix}\\ detB_1=b_1C_{11}+b_2C_{21}+\dots+b_nC_{n1}=C^Tb的结果向量的第一个元素\\ B_J=A的第j列由b替代$

通过行列式求体积：三维空间体的点坐标向量组成A矩阵
$\left|\begin{array}{c} detA \end{array}\right|=V$
如果能够证明箱子体积具有行列式的三性质，而三性质定义了行列式，则体积一定等于行列式

正交矩阵对应的箱子是立方体（与单位矩阵相比被旋转了）
$\because detQ^TQ=detI=1\\ \left|\begin{array}{c} Q^T \end{array}\right| \left|\begin{array}{c} Q \end{array}\right|= \left|\begin{array}{c} Q \end{array}\right|^2=1\\ \therefore detQ=\pm 1$

对于面积：

任意三角形面积：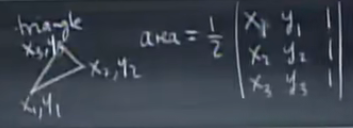

特征值和特征向量

特征向量&特征值：
$\Rightarrow Ax=\text{特征值}\lambda \text{ 特征向量}x$
A为奇异矩阵时，lambda=0时一个特征值

投影矩阵P，b不再平面上，Pb为投影，此时b不是特征向量，一位Pb!=lambda b，而平面上向量x是特征向量Px=x、特征值=1，同时x垂直于平面时，Px=0x、特征值=0

置换矩阵：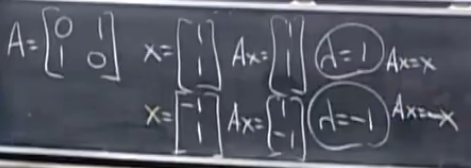

迹：特征值的和=矩阵的对角线元素的和

$KaTeX parse error: Expected 'EOF', got '&' at position 35: …-\lambda I)x=0 &? \text{ 此时(A-la…$

$当有Ax=\lambda x 和Bx=\alpha x\\ 无法得出(A+B)x=(\lambda + \alpha)x\\ 因为B的特征向量不一定与A相同，除非B是单位矩阵的倍数$

$Ax=\lambda x\\ (A+nI)x=\lambda x + nx=(\lambda + n)x\\ x是A和(A+nI)共同的特征向量$

$det=\lambda_1\lambda_2 \dots \lambda_n$

即使矩阵是实数组成，其特征值有可能是负数

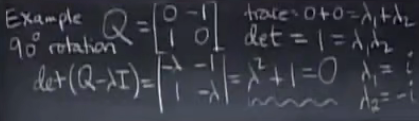
矩阵需要时对称或接近对称的，特征值才是实数

三角阵特征值在对角线上

退化矩阵：特征向量短缺（无无关的特征向量），特征值重复

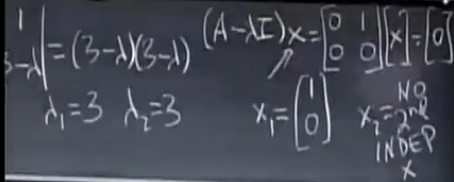
对角化和A的幂

A的特征向量组成的矩阵S
$\begin{aligned} AS&=A \begin{bmatrix} x_1 & x_2 & \dots & x_n \end{bmatrix}\\ &= \begin{bmatrix} \lambda_1x_1 & \lambda_2x_2 & \dots & \lambda_nx_n \end{bmatrix}\\ &= \begin{bmatrix} x_1 & x_2 & \dots & x_n \end{bmatrix} \begin{bmatrix} \lambda_1 & 0 & \dots & 0\\ 0 & \lambda_2 & \dots & 0\\ \dots & \dots & & \dots\\ 0 & 0 & \dots & \lambda_n \end{bmatrix}\\ &=S\Lambda \end{aligned}$
对角化：
$S^{-1}AS=\Lambda\\ 前提A有n个线性无关的特征向量$
A的幂：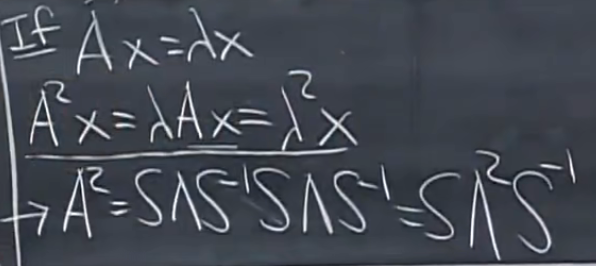

A平方，特征向量不变（S不变）特征值平方（Lambda²）

eg：斐波那契数列

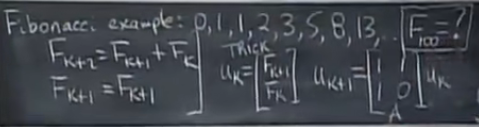
$u_{k+1}=Au_k\\ u_k=A^ku_0$

把二阶标量方程转化为了一阶向量方程组

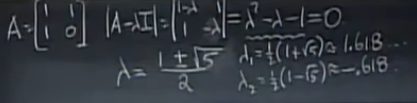
数列的增长由（较大的）特征值决定

回代特征值求出特征向量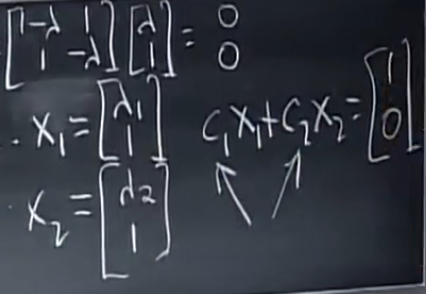

此时S已知，Lambda 也已知，可以求
$A^k=S\Lambda^k S^{-1}$
求出A^k即可求出U_k

以u₀为例可以得到c₁x₁+c₂x₂=u₀=(1 0)

对于动态增长的一阶方程组，初始向量是u₀，关键在于确定A的特征值及特征向量，特征值决定增长的趋势，把u₀展开成特征向量的线性组合，且各个特征向量必须独立

这种递推关系就是差分方程

微分方程和exp(At)

利用特征值和特征向量来求解常系数线性微分方程

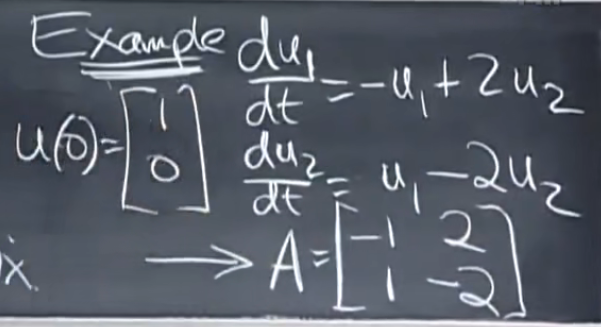
一开始所有都在u₁（u(0)第一个元素为1），随着时间推移，有du₂/dt > 0，东西会从u₁处流到u₂，随着时间我们追踪它的变化

A为奇异矩阵，所以有个特征值为0，根据迹可知特征值和为-3，所以另一个特征值为-3

求出特征向量

解：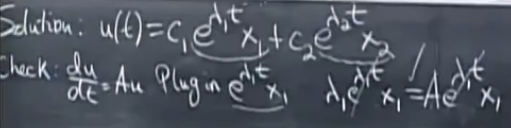

纯解（e^lambdatx）纯指数形式是纯幂形式在微分方程中的类似体
$u(t)=c_1e^{\lambda_1t}x_1+c_2e^{\lambda_2t}x_2 \simeq c_1\lambda_1^kx_1+c_2\lambda_2^kx_2$
求c₁c₂：
$代入特征值和特征向量得u(t)=c_1 \begin{bmatrix} 2\\ 1 \end{bmatrix}+ c_2e^{-3t} \begin{bmatrix} 1\\ -1 \end{bmatrix}\\ Sc=u(0)$

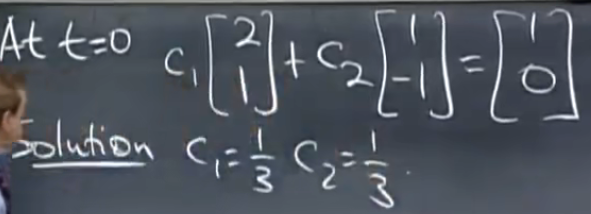
当t趋于无穷时，即稳定状态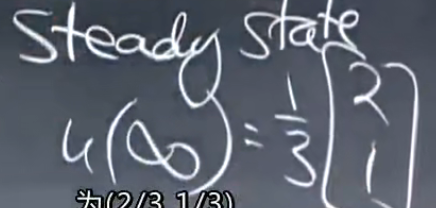

但是稳定状态不是什么时候都有的

稳定性：由lambda的实部决定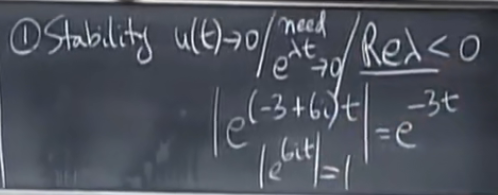

稳态：有一个特征值=0，并且其他特征值的实部<0，如果有任何特征值的实部>0，则解u(t)无法收敛

2阶系统，根据矩阵直接判断特征值实部符号：正的行列式（特征值符号相同），负的迹（特征值和小于零）

原方程组有两个相互耦合的未知函数u₁u₂，特征值和特征向量的作用是解耦，又称对角化
$KaTeX parse error: Expected 'EOF', got '&' at position 154: …}=\lambda_1v_1 &? \frac{dv_2}{dt…$

$v(t)=e^{\Lambda t}v(0)\\ u(t)=Se^{\Lambda t}S^{-1}u(0)=e^{At}u(0)$

e^At是原方程的解，矩阵指数

定义矩阵指数：将指数展开成幂级数的形式（泰勒级数）
$两个泰勒级数：\\ e^x=\sum\frac{x^n}{n!} \Rightarrow e^{At}=I+At+\frac{(At)^2}{2!}+\frac{(At)^3}{3!}+\dots+\frac{(At)^n}{n!}\\ \frac{1}{1-x}=\sum x^n \Rightarrow (I-At)^{-1}=I+At+(At)^2+(At)^3+\dots+(At)^n$
第一个级数总是收敛的，而第二个要看A的特征值是否小于1，小于才收敛，第一个级数更好
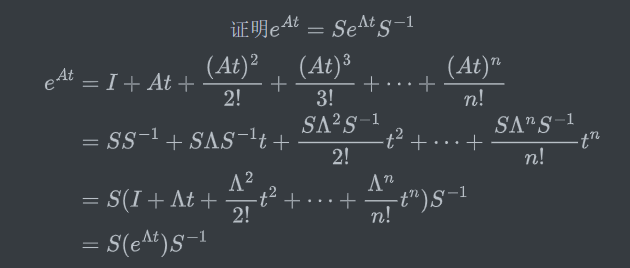
在这里插入图片描述

前提是A有n个特征值，即A可以对角化
$e^{\Lambda t}=\begin{bmatrix} e^{\lambda_1t} & 0 & \dots & 0\\ 0 & e^{\lambda_2t} & \dots & 0\\ \dots & \dots & & \dots\\ 0 & 0 & \dots & e^{\lambda_nt} \end{bmatrix}$
何时矩阵指数收敛于0：当t不断增长，e^At趋近于0，S是常数矩阵，不变，e^Lambda*t趋近于0，说明对角线上元素收敛于0，即lambda的实部<0，此时矩阵指数稳定

复平面：

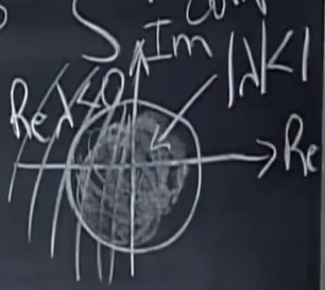
圆中的是特征值的绝对值<1，使得矩阵的幂稳定，斜线是特征值的实部<0，使得矩阵指数稳定

将二阶微分方程化成一阶方程组：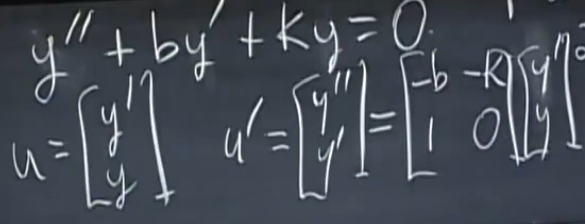

马尔科夫矩阵傅里叶级数

特征值的应用

马尔科夫矩阵性质：

矩阵所有元素大于等于0
每个列，元素相加等于1<=>一个特征值为1
- A-1I，可以发现(A-1I)的每个列，元素相加为0，所以A-I是奇异矩阵（其所有行加到最后一行上产生零行，即行线性相关，行列式为0），所以转置的马尔科夫矩阵的特征向量很好求，为(1 1 1)，特征值可求为1，马尔科夫矩阵的特征值也为1

A和A^T的特征值是一样的：转置前后矩阵行列式相等可得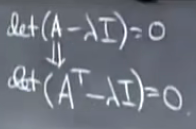

马尔科夫矩阵的应用：考察概率，所以所有元素大于等于0，介于0~1。整个系统没有外界输入，所以列加起来为1

考察麻省和加州的人口变迁：每次变动概率一样，表现为马尔科夫矩阵不变

在k+1时刻，对于加州，0.9的人留在加州，0.1的人搬去了麻省。而对于麻省，0.8的人留在麻省，0.2的人去了加州

求经过100步变迁后人口情况u₁₀₀=A¹⁰⁰u₀：

求马尔科夫矩阵特征值和特征向量

矩阵求幂的结果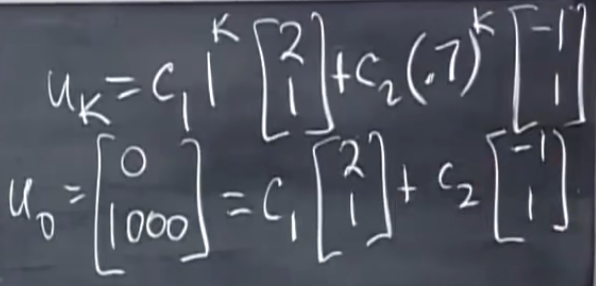

可得c₁和c₂，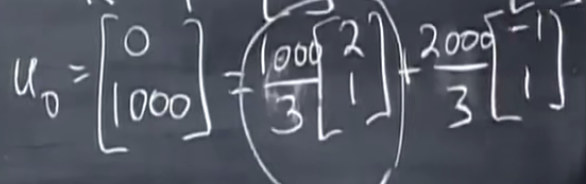

随着步数增多，特征值为0.7的部分将会趋近于零，只留下特征值为1的

有些教材是行向量元素相加为1

有一组标准正交基q₁,…,q_n，任意v由基线性组合产生，而v乘某一基向量的转置（做内积），就将其他项消除了（内积为0）而只保留了特定基向量的项：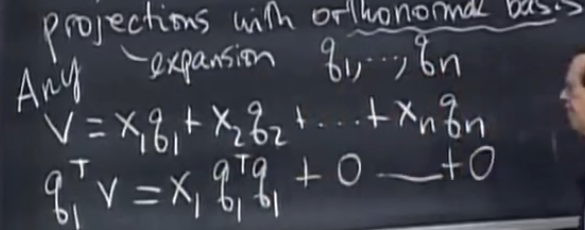

傅里叶级数：
$f(x)=a_0+a_1\cos x+b_1\sin x+a_2\cos2x +b_2\sin2x+\dots$
可以用函数f(x)来代替向量v，用正交函数来代替正交向量q₁q₂…，因此基是1，cosx，sinx，cos2x等

傅里叶级数成立的原因是它们是正交的

函数正交：内积为0，在向量中内积是离散的元素相乘加和，而对于连续的函数，内积是函数相乘的从0到2pi的积分

与消除向量同理，f(x)整体与某项的函数（如cosx）做内积可以消除除某项外的其他函数项
$\begin{aligned} \int^{2\pi}_0f(x)\cos xdx&=a_1\int^{2\pi}_0(\cos x)^2dx=a_1\pi\\ \text{傅里叶级数系数公式 }\frac{1}{\pi}\int^{2\pi}_0f(x)\cos xdx &= a_1 \end{aligned}$

复习二

三个点拟合到过原点的直线上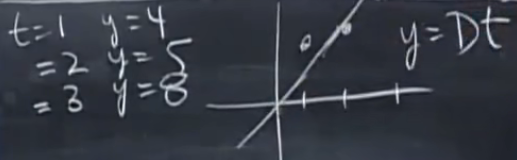

特征值不为零，矩阵可逆

$detA^{-1}=\frac{1}{\lambda_1\lambda_2\lambda_3\dots\lambda_n}\\ trace(A+I)=(\lambda_1+1)+(\lambda_2+1)+\dots=\lambda_1\lambda_2+\dots+\lambda_n+n$

文章来源:https://blog.csdn.net/Falling_Asteroid/article/details/134958496
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：veading@qq.com进行投诉反馈，一经查实，立即删除！

MIT18.06线性代数 笔记2