正交调制与解调原理

一、正交调制与解调原理

? ? ? ?? ? ? ? ? ? ? ??

/***************************************正交调制*********************************************/

图中信道中的信号为：s(t)=sR?(t)cos(w0?t)?sI?(t)sin(w0?t)（这就是正交调制后的信号）

我们可以通过傅里叶变换得到：S(w)=12?[(SR?(w?w0?)+SR?(w+w0?))+j(SI?(w?w0?)?SI?(w+w0?))]

此时频谱分析发现，频率分量变化了，当w0的值较大时，信号频率变成高频，可知w0，决定的是调制后信号振动的频率（通俗讲就是上下摆动的密度）（w0由调制信号cos(w0?t)

和sin(w0?t)所决定）。调制完成

/***************************************正交解调*********************************************/

由信道中的信号：s(t)=sR?(t)cos(w0?t)?sI?(t)sin(w0?t)乘以2cos(w0?t)得到：

2cos(w0?t)[sR?(t)cos(w0?t)?sI?(t)sin(w0?t)]。

对其傅里叶变换进行频谱分析得到：

12??[(SR?(w?2w0?)+SR?(w)+SR?(w)+SR?(w+2w0?))+j(SI?(w?2w0?)?SI?(w)+SI?(w)?SI?(w+2w0?))]

经过低通滤波器，滤除2w0?的频率分量，则只剩下SR?(w)。复原了原信号。

同样的：

由信道中的信号：s(t)=sR?(t)cos(w0?t)?sI?(t)sin(w0?t)乘以2 sin (w0?t)得到：

2 sin (w0?t)[sR?(t)cos(w0?t)?sI?(t)sin(w0?t)]。

对其傅里叶变换进行频谱分析得到：

2j?[(SR?(w?2w0?)+SR?(w)?SR?(w)?SR?(w+2w0?))+j(SI?(w?2w0?)?SI?(w)?SI?(w)+SI?(w+2w0?))]

经过低通滤波器，滤除2w0?的频率分量，则只剩下SI??(w)。复原了原信号。

二、IVUS的应用

在我们IVUS系统中，声波发射的不是单个脉冲，而是发送好几个脉冲信号，在经过人体不同物质返回回声时，因为多个脉冲信号，返回的信号是如下图所示

该信号需要经过正交解调后得到该信号的包络（如图红线部分），从而分辨出该物质密度和体积等信息。如下图红色线部分。

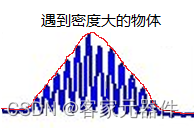
上面调制过程中有IQ两个分量，在IVUS系统中将其中一个分量设为0即可对应上面的原理。