数独 -- 合法数独与完全数独
一、数独的介绍
????????从2004年底开始,数独游戏在英国变得非常流行。数独(Sudoku)是一个日语单词意思是数字位置之类的单词(或短语)。谜题的理念非常简单;面对一个9 × 9的网格,被分成9个3 × 3的块:

????????在其中的一些盒子里,设置者放一些数字1-9:求解者的目的是通过在每个盒子里填一个数字来完成网格,这样每一行,每一列,每个3 × 3的盒子都只包含1-9的每个数字一次。
? ? ? ? 在这里,我们讨论枚举所有可能的数独网格的问题。这是一个非常自然的问题,但是,也许令人惊讶的是,这个问题似乎不太可能有一个简单的组合答案。事实上,数独网格只是拉丁方格的特殊情况,拉丁方格的枚举本身就是一个难题,没有已知的一般组合公式。已知9 × 9的拉丁平方数为5524751496156892842531225600 ≈ 5.525 × 10^27。由于这个答案是巨大的,我们需要大大改进我们的搜索,以便能够在合理的计算时间内得到答案。
1、初步观察
我们的目标是计算有效数独网格的数量。在下面的讨论中,我们将把这些块称为B1-B9,它们被标记在这里:

????????首先注意,在重新标记之后,我们可以假设左上角的块(B1)是由:
对于任意一个合法数独,我都可以通过1-9数字的一对一映射,将B1块转化为这种标准形式,例如:
? ? 转化为? ??
按照:4→1、5→2、8→3、1→4、7→5、9→6、2→7、3→8、6→9即可得到这种标准形式
????????这种重新标记过程将网格的数量减少了9! = 362880倍。我们被简化为计算左上角是这种标准形式的非数独网格的数量。
????????从广义上讲,我们的策略是考虑所有可能的方法来填充块B2, B3,因为B1是上面的规范形式,将问题减少到较小的搜索空间。这形成我们强力搜索的外环。对于内部循环,我们找出所有可能的方法来完成块B2和B3转换为全网格。
2、B2块和B3块
????????在这里,我们尝试有效地对B2块和B3块的可能性进行分类。我们将对如何找到一个相对较小的B2块和B3块列表进行长时间的讨论,这将使我们能够给出最终答案。(其中一些缩减也可以应用于B4和B7块,以加快搜索速度,尽管一旦B2/B3固定,许多缩减步骤不能以同样的方式在B4/B7上执行)。
2.1、最上面一排积木
我们想要列出前三个块的所有可能配置,假设第一个块是标准形式。我们来看看第二个块的最上面一行。它要么由(以某种顺序)B1块的第2行或第3行的三个数字组成,要么是两者的混合。我们将这种情况称为“纯净”和“混合”情况。B2块和B3块可能的顶行由下式给出:

(其中{a, b, c}表示数字a, b和c的任意顺序)。
纯净顶行{4,5,6} {7,8,9}可以补全如下:
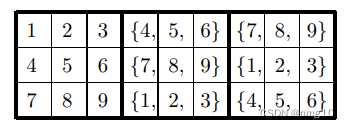
得到 (3!)^6 【注:一个{}中有3!种排列,B2和B3共6个{}】可能的配置。
然而,混合顶行可以通过多种方式完成;例如,最上面的行{4,5,7} {6,8,9}可以补全为:

其中a, b和c分别代表1,2和3,以某种顺序,给出 3×(3!)^6 种可能的配置(b和c是可互换的,及abc等价acb,所以abc的组合就3种)。
为什么下图红框内是{8, 9, a}
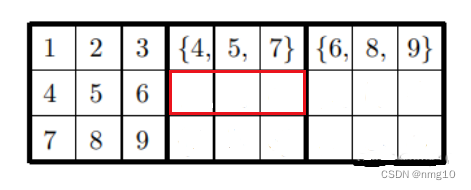
首先我们应该清楚,这个红框初步来看,应该是可以填{1,2,3,8,9},然而第一行和第三行中已经有{8,9}了,所以{8,9}必有,然后{1,2,3}任选其一,所以红框内是{8, 9, a}。同理可分析剩余3组,得到的就是 (图3) 的结果。
我们有2个纯净顶行和18个混合顶行(图1)。
因此,总的来说,我们有2*(3!)^6+18*3*(3!)^6=56*(3!)^6 = 2612736个可能的补全到前三块。
2.2、优化减少外部循环
????????在这个阶段,我们有一个B2块和B3块的所有可能性的列表。我们将遍历所有这些可能性,并为每个可能性填充剩余的块以形成有效的数独网格。外部循环将运行可能的B2块和B3块。然而,遍历B2和B3的所有 (2612736 种) 可能性将非常耗时。我们需要某种方法来减少我们必须循环的可能性的数量。我们将在这些块中确定数字的配置,这些配置为完整的网格提供了相同数量的完成方式。有效地,我们定义了B2/B3组态集合上的等价关系,使得同一类中的任意两个元素可以以相同数量的方式完成。
????????幸运的是,我们可以应用很多操作来保持数独网格的数量不变。我们已经看到了重新标签的操作。但也有其他的,例如,如果我们交换B2和B3,那么每一种将B2-B3完成为完整网格的方式都会给我们一种将B3-B2完成为完整网格的唯一方式(只需交换B5和B6,以及B8和B9)。事实上,我们可以用任何我们选择的方式排列B1 B2和B3(尽管这改变了B1,但我们可以重新标记使B1回到标准形式)。此外,我们可以以我们希望的任何方式排列任何块中的列,对完整网格中的列执行相同的操作。我们看到B1-B3上有许多操作,这些操作给出了其他可能的顶部块,它们以相同数量的方式完成完整的网格。
2.2.1 辞典编纂的减少
取上面提到的 2612736 种可能性。我们首先将它们分类如下:
????????1. 我们首先对B2和B3中的列进行排列,使第一个项按递增顺序排列。
????????2. 然后,如果有必要,我们交换B2和B3,这样在字典中B2就会出现在B3之前(“词典顺序”)。
第一步将原本是3!种排列变成了1种递增顺序的排列,有B2和B3两个块,这样,给定任何一个网格,有(3!)^2 = 36 个网格衍生出相同数量的完成方法。
第二步是将B2B3或B3B2变成一种递增词典顺序,及减少两倍。
????????总的来说,我们将需要考虑的可能性数量减少了72倍,我们的目录中有 2612736/72=36288 种可能性。这将我们的搜索减少到36288,这是可行的,尽管更多的减少是可取的。
然而,它为我们的缩减提供了一个良好的开端,将我们的目录缩减到可以更好地控制单个条目的大小。
2.2.2 精致的排列和重新标签
????????事实上,我们还没有充分利用所有的排列和重新标记的可能性。其思想是遍历36288种可能性的三个块B1-B3的所有排列3!,以及这三个块中所有列的排列3!^3,使每个有6^4 = 1296种可能性。
????????然后,我们查看新的第一个块,并重新标记它,使其成为标准形式,类似地重新标记B2和B3,然后对结果使用字典法约简。这再次提供了一个巨大的改进,将目录的大小减少到只有2051个可能的B2/B3对。(这2051对中的绝大多数恰好来自36288种可能性中的18 = 6^4/72。然而,有些是由更少的可能性产生的,因此有必要准确存储36288种可能性中产生给定块的可能性。)但这还不是全部我们可以对构型的三行进行3!种排列。也就是说,我们可以选择这些行的任意排列,然后将B1重新标记为标准形式。这进一步减少了测试区块B2和B3的416种可能性。
上面说的2051种或416种可能性,这些需要进行程序遍历才能得到,不能理解那我举一个例子,你可能就明白了:
现在有两个【B1B2B3】的组合,它们两都是36288中的一种可能。
S1?? ??? ??? ??? ??? ?S2
123 456 789?? ??? ??? ?123 456 789?? ??? ?
456 789 123?? ??? ??? ?456 978 312
789 231 564?? ??? ??? ?789 312 645
我们可以通过交换1、3两行,然后标准化和B2B3顺序化,使得它们等价
交换S2的1、3两行 R(1,3),得到
789 312 645
456 978 312
123 456 789
然后将B1标准化,得到【1->7,2->8,3->9,4->4,5->5,6->6,7->1,8->2,9->3】
123 978 645
456 312 978
789 456 123
再然后B2、B3首列排序【978->789 645->456 第二列和第三列也要跟着动哦!】
123 789 456
456 123 789
789 564 231最后将B2与B3首列首个数字排序【7>4 交换B2和B3块】
123 456 789
456 789 123
789 231 564
这个是不是就和S1一样了
所以这就是减少可能组合的过程,全部的36288个我们只有通过程序将它们都找出来现在你懂的起了吧!
2.2.3 深度优化减少外部循环
虽然这种改进非常有用,但我们能做的削减越多,程序完成得就越快。的确,改善我们的外循环还有更多的可能性。下面是数独格子中最前面三行可能的排列方式:
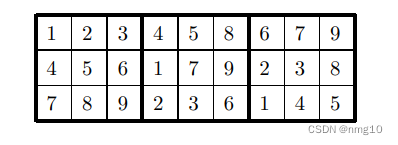
考虑数字1和4的位置:
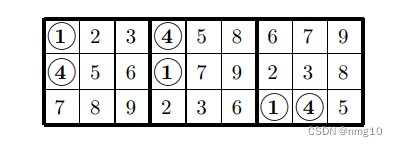
让我们重新标记以交换这两个数字:
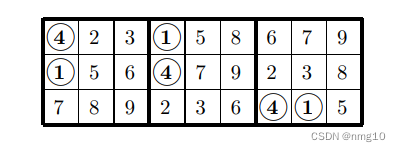
很容易看出,任何完成这三个方块的网格也完成了相同的三个方块,在B1/B2中,1和4颠倒了:
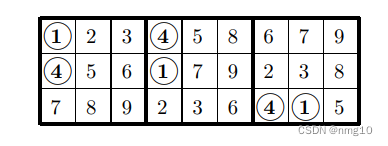
因此,扩展原始三行的方法数与扩展这三行的方法数相同,因此我们只需计算一次。请注意,对于第2列和第9列中的数字5和8,以及第3列和第6列中的数字6和9,也可以执行相同的操作。我们要求B1的一列中的两个数字在B2/B3的一列中出现在相同的位置(当然,顺序相反)。然后,我们可以交换这些数字的其他两次出现。以下排列允许不少于六对数字:

该方法的扩展允许我们识别具有大小为2 × k(分别为k × 2)的子矩形的任意两个配置,其条目由具有相同数字的两列(分别为行)组成。
仅对2x2个子矩形使用此技巧将416个等价类减少到174个。使用2 × 3,3 × 2和4 × 2矩形可将这个列表减少到只有71个类。
这就完成了我们对区块B2和B3的讨论。
2.3、外部B1B2B3块的结论
编写了一个lua程序,生成所有36288个按字典顺序约简的配置,然后基于上述等价关系构建等价关系,即确定这些等价关系生成的关系的自反性、对称性和传递性外壳。然后程序生成一个代表类的列表和每个等价类的大小。实际上,选择的代表是对应等价类的字典顺序最小的成员。在最初的计算中,并非所有这些等价都实现了;我们将外部循环减少到运行306个类。随后,这些程序又在71名代表中进行了一次运行。得到的答案是一样的。

以下是71个类:
[456789,789123,123456]、[456789,789123,123465]、[456789,789123,123564]
[456789,789123,132465]、[456789,789123,132546]、[456789,789123,132564]
[456789,789123,231564]、[456789,789123,231645]、[456789,789132,123546]
[456789,789132,132546]、[456789,789132,213456]、[456789,789132,213546]
[456789,789132,213645]、[456789,789132,213654]、[456789,789132,231546]
[456789,789132,231564]、[456789,789132,231645]、[456789,789231,123645]
[456789,789231,132546]、[456789,789231,231564]、[456789,789231,231645]
[456789,789231,312456]、[456789,798132,213546]、[456789,798132,213645]
[456789,798132,231546]、[456789,798213,213564]、[456789,798213,213654]
[456789,897312,312564]、[457689,189237,263145]、[457689,189237,263154]
[457689,189237,263514]、[457689,189237,362145]、[457689,189237,362154]
[457689,189273,263145]、[457689,189273,263154]、[457689,189273,263514]
[457689,189273,362154]、[457689,189273,623154]、[457689,189273,632154]
[457689,189273,632514]、[457689,189327,362145]、[457689,189723,623145]
[457689,189723,623154]、[457689,189723,623514]、[457689,189723,632154]
[457689,189732,623514]、[457689,198723,236514]、[457689,198723,326514]
[457689,198723,632514]、[457689,198732,632514]、[457689,289137,361245]
[457689,289137,361254]、[457689,289137,631524]、[457689,289173,163452]
[457689,289173,613245]、[457689,289173,613254]、[457689,289731,163245]
[457689,289731,613254]、[457689,289731,613542]、[457689,298137,316245]
[457689,298137,316254]、[457689,298713,316245]、[457689,389271,612534]
[457689,389712,612345]、[457689,398217,126345]、[457689,398217,612345]
[457689,398721,126345]、[457689,398721,216354]、[457689,398721,612345]
[457689,891723,236514]、[457689,893271,216354]看不懂是吧,我教你
对于[457689,893271,216354]
结果为
B2? ?B3
457 689
893 271
216 354
B1不用说当然是标准形式啦,完整的是
?B1? B2? B3
123 457 689
456 893 271
789 216 354
3、内循环
3.1、左侧的块:B4和B7
????????对左列的完全相同的分析给出了左三列的可能补全数为56 x(3!)6 = 2612736(再次假设左上角的块是规范形式)。同样,我们可以对B4的行进行排列,或对B7的行进行排列,或交换B4和B7,使用词典法约简方法将其减少72倍至36288。上述一些缩减方法可用于进一步缩减B4/B7目录的规模。
????????然而,在这个阶段,我们已经充分减少了B2/B3目录的大小,因此不需要对B4/B7目录进行完全优化。实际上,编写程序的第一作者认为,只对B4和B7的720个可能的第一列(第一列中剩余数字{2,3,5,6,8,9}的所有排列)运行循环更简单。同样,通过重新排序B4和B7的行,并在必要时交换B4和B7,我们将这些第一列的可能性减少到只有10种,而不存储其余的数据。如前所述,此时预测的运行时间非常低——在单个PC上只有几个小时——因此,通过循环处理所有区块B4和B7的可能性目录所获得的可能的加速,通过上面列出的一些方法减少,几乎不值得实现。
3.2、内部循环的策略
在此阶段,填充最上面的三个块B1-B3,以及块B4和B7的第一列。第一作者编写了一个回溯算法,运行按以下顺序输入数字的可能性:

这个顺序是基于观察到每个数独方格也是一个拉丁方格。为了保持较低的分支因子,最好从剩余最短的列或行开始创建条目。
这被证明是一种非常有效的方法,在一台PC上耗尽了给定配置的区块B2和B3的可能性,只需不到2分钟。
二、研究结果简写
存在No = 6670903752021072936960≈6.671 x10^21个有效数独网格。去掉9!和72^2来自块B2和B3的顶行的重新标记和字典化缩减。在块B4和B7的左列中,这就留下了3546146300288 = 2^7 x 27704267971的排列,最后一个因子是素数。
三、最后的最后
数独是一个很有趣的益智游戏,很早我就喜欢它了,这也是我研究它的原因,我们现在只是完成了合法数独生成,但是我们还需要研究如何解题,这才是最重要的,以及如何生成一个让大家头疼的数独题,也是只得我们研究学习的,后面我也会继续对解数独和创建数独题进行思考研究。有兴趣的小伙伴也可以一起进群来讨论学习。
群名称:美丽的数独_sudoku
群? ?号:922514302

本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!

