机器学习之全面了解回归学习器
我们将和大家一起探讨机器学习与数据科学的主题。
本文主要讨论大家针对回归学习器提出的问题。我将概要介绍,然后探讨以下五个问题:
1. 能否将回归学习器用于时序数据?
2. 该如何缩短训练时间?
3. 该如何解释不同模型的结果和可用的绘图?
4. 我选择了具有最小均方根误差 (RMSE) 的模型;接下来还需要做些什么?
5. 如何基于新数据进行预测?
本文会解答一些有关 MATLAB 回归学习器的问题,基本上不涉及回归本身。
引言
自 2017 年起,工程师和科学家可以在 MATLAB 中使用回归学习器。
回归分析可以帮助人们理解变量和数值响应之间的关系,可用于预测能耗、财务绩效和制造工艺参数等。从根本上说,有了回归学习器,您无需编写代码即可交互构建回归模型,并衡量模型的准确度和性能。
您可以快速比较各种回归模型和特征的性能。这款 App 对于刚接触机器学习的人特别有用,因此我很高兴回答一些与该 App 直接相关的问题。
Q1
能否将回归学习器用于时序数据?
当然可以。
例如,您可以使用回归模型来预测电力负荷或预测暴风雨造成的损失,与在其他机器学习 App 中一样,在该 App 中使用时序数据之前,必须对数据进行预处理和清理。
这包括将数据调整到正确的格式、对数据进行归一化以使其处于同一尺度、均匀地分布数据、处理重复数据或缺失数据,以及执行其他必要任务。


Q2
训练花费的时间太长;我该怎么做才能更快地训练我的模型?
您可以在回归学习器中执行几项操作来加快训练速度。提醒一下,在这里我主要介绍该 App 本身提供的方法。
建议 1:使用并行回归模型训练
如果您拥有 Parallel Computing Toolbox?,首先可以尝试的是使用并行回归学习器模型进行训练,这也是比较简单的方法。此方案会创建一个并行池以进行并行训练,让您能够在继续工作的同时并行训练多个模型。
如果选择此方案,您将在“历史记录”列表中看到每个训练中模型和排队中模型的进度指示器,并且还可以随时取消某个模型。这种方法将有助于减少训练所需时间。

在回归学习器的菜单栏中选择“使用并行”。
建议 2:使用留出法验证
如果数据很大,请确保使用正确的验证选项。
当您在回归学习器中打开新会话并选择数据时,默认会选择交叉验证。
交叉验证可将数据划分为若干折 (k)、训练模型并计算所有折的平均测试误差。
与其他方案相比,此方法可以更好地防止过拟合,但需要多次拟合,因此适用于中小型数据集。
留出法验证可让您使用滑块控件选择要用作测试集的数据百分比。该 App 将在训练集上训练模型,并通过测试集评估其性能。用于测试的模型仅基于一部分数据,因此留出法验证特别适用于大型数据集。当然,您也可以选择不验证模型,但是这有可能导致训练数据过拟合。了解有关回归问题验证选项的更多信息

启动新会话时,默认会选择交叉验证。
建议 3:仅在一组模型类型上训练数据
如果您已知数据特别适合用某一类模型处理,或者某一类模型的训练速度太慢,则可以在 App 中选中该类型或取消选中,而不必对所有类型进行训练。如果不确定,则可以尝试“全部(快速训练)”选项,该选项将对所有训练速度通常较快的模型类型进行训练。
然后,您可以训练均方根误差 (RMSE) 最小的那一组的所有模型,以找到最佳模型。
建议 4:精简训练数据
人们经常讨论如何获得足够的数据,但其中的关键是确保拥有足够的正确数据。您可能有一些多年前的历史数据,一些不必要、不再有用的数据。
删除或减少这类数据可以加快训练速度,当然,您需要时刻关注数据的准确性和代表性。这应该是您最后的选择,因为您必须非常谨慎地减少数据。
Q3
该如何解释不同模型的结果和可用的绘图?
这是一个很好的问题!
在用您的数据训练完模型后,需要采取几个步骤来解释结果。
步骤 1:找出具有最小均方根误差的模型
RMSE 衡量每个模型的预测值与观测值之间的距离,因此它衡量的是这些残差的扩散程度。该 App 将在最小 RMSE 周围加一个框。
步骤 2:探查模型
选择具有最小 RMSE 的模型后,下一步就是查看 App 中可用的不同绘图:常用的绘图有两种:响应图,实际值-预测值图。

较小的 RMSE 将以粗体显示,并带有一个方框。
响应图
响应图以竖线显示预测响应与观测值之间的差异。如果您对数据使用留出法验证或交叉验证,则此图特别有用,因为图中显示的预测值对应的是留出的观测值,模型未在这部分数据上进行训练。

使用响应图查看预测值和观测值之间的距离。
实际值-预测值图
实际值-预测值图可帮助您检查模型性能。该图绘制了模型的预测响应对真实响应的图。
在此图中,理想的回归模型应有与观测值相同的预测响应,因此所有点都将位于对角线上。
然而,这在现实中是不可能的,所以我们的目标是让这些点尽可能靠近对角线,并大致对称地分散在对角线附近。如果能在此图中检测到模式,则意味着模型可以改进,您可以选择训练其他模型类型,也可以选择使用高级选项使模型更灵活。
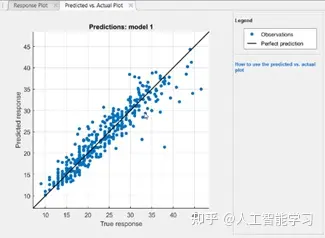
实际值-预测值图可帮助您可视化回归模型的准确度。
Q4
我选择了具有最小均方根误差 (RMSE) 的模型;要优化模型,接下来还需要做些什么?
在针对数据训练和评估初始模型之后,可以通过调整模型的超参数来确保实现最佳性能。
要自动选择并找到模型的最佳超参数值,可以使用超参数优化功能。
该 App 会尝试不同的超参数值组合,以最小化模型的均方误差 (MSE),并返回使用优化超参数的新模型。
超参数调整的效果因模型而异,因此您需要为多种类型的模型优化超参数,因为初始模型可能无法实现最佳性能。
Q5
如何开始进行预测?
要使用经过全面训练和优化的模型基于新数据进行预测,您需要将模型导出到某个位置。您可以将其导出到 MATLAB 工作区,或者生成 MATLAB 代码,以使用刚才在 App 中所用的步骤来训练模型。
然后,您可以使用 MATLAB Compiler? 部署模型,或者使用 MATLAB Coder? 从模型生成 C/C++ 代码。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!