贪心算法:买卖股票的最佳时机II 跳跃游戏 跳跃游戏II
2023-12-13 06:00:48
122.买卖股票的最佳时机II?
- 思路:
- 想要获得利润,至少要以两天为一个交易单元,因为两天才会有股价差。
- 因此可以将最终利润进行分解,如prices[3] - prices[0] =?(prices[3] - prices[2]) + (prices[2] - prices[1]) + (prices[1] - prices[0]),也就是把利润分解为每天为单位的维度,那么就可以很清晰地看出,哪些天有收益,哪些天是亏损,而要获得最大利润,只需要收集所有正利润。
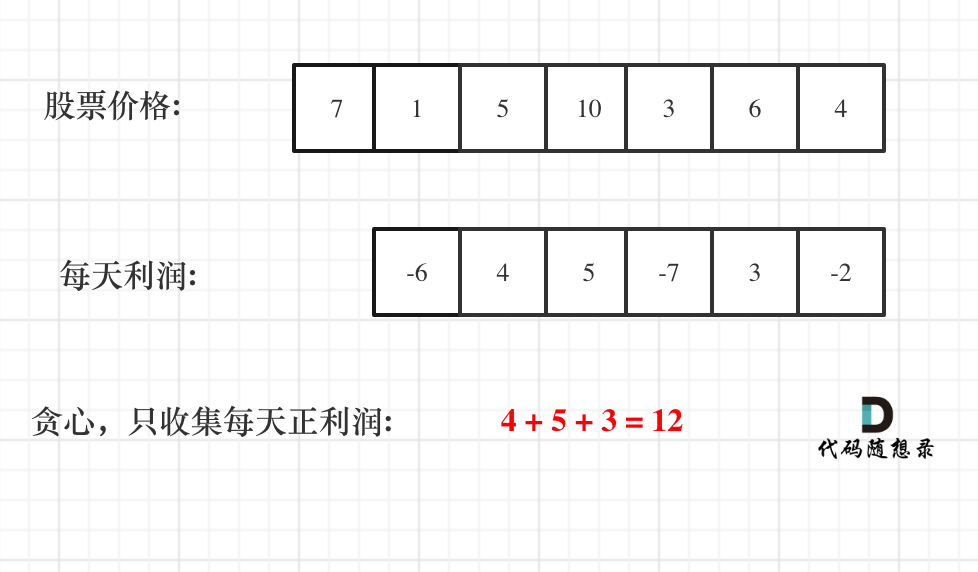
- 局部最优:收集每天的正利润,全局最优:求得最大利润。
- 时间复杂度:O(n)
- 空间复杂度:O(1)
class Solution {
public:
int maxProfit(vector<int>& prices) {
int res = 0;
for(int i = 1; i < prices.size(); i++) {
if(prices[i] - prices[i - 1] > 0) {//只统计正利润
res += prices[i] - prices[i - 1];
}
// res += max(prices[i] - prices[i - 1], 0);//也可以这样写
}
return res;
}
};55.?跳跃游戏
- 思路:
- 本题关键在于可跳的覆盖范围,即每次取最大的跳跃步数,只要终点在可以跳到的覆盖范围之内,那么就一定能跳到终点。
- 做法:
- 每次移动取最大跳跃步数(得到最大的覆盖范围),每移动一个单位,就更新最大覆盖范围。i只能在覆盖范围cover内遍历,每移动一个元素,cover 得到该元素数值(新的覆盖范围)的补充,让 i 继续移动下去。而cover更新时,取cover和新的覆盖范围的较大者。如果 cover 大于等于了终点下标,说明可以到达最后一个位置,直接 return true 。
- 贪心算法局部最优解:每次取最大跳跃步数(取最大覆盖范围)。
- 整体最优解:最后得到整体最大覆盖范围,看是否能到终点。
- 时间复杂度: O(n)
- 空间复杂度: O(1)
class Solution {
public:
bool canJump(vector<int>& nums) {
int cover = 0;
if(nums.size() == 1) return true;
for(int i = 0; i <= cover; i++) {
cover = max(i + nums[i], cover);
if(cover >= nums.size() - 1) return true;
}
return false;
}
};参考链接
代码随想录:最买卖股票的佳时机II? 跳跃游戏?
文章来源:https://blog.csdn.net/m0_59425585/article/details/134950939
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!