机器人相关知识

机器人的分类

机械臂机器人

串联机器人

就是每一节机械臂之间通过关节轴链接成为一串机械臂的一组机械臂。

并联机器人

电机并不是像串联机器人一样，一个电机+一个连杆+一个电机，这种方式连接起来。而是各自电机控制各自独立的连杆，所有连杆末端共同控制一个末端执行器。

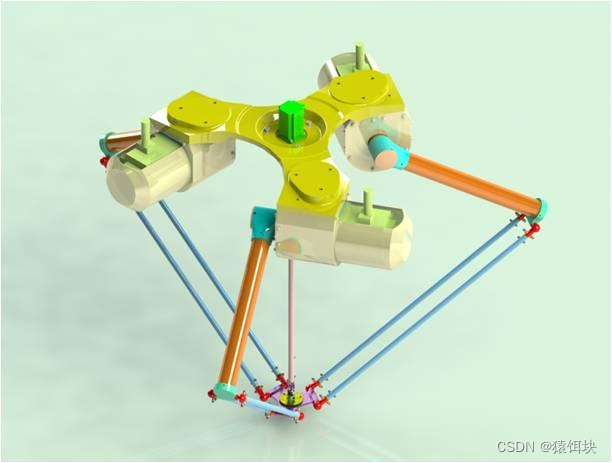
混合机器人

机器人学需要线性代数的矩阵基础

线性代数

向量的点积

点乘和叉乘

矩阵满足结合律，不满足交换律。

满足交换律的是逆矩阵。

旋转矩阵

平移矩阵

行列式值的几何意义

二阶行列式是在二维中的平行四边形；

三界行列式是三维中的六面体的体积；

矩阵的几何意义

矩阵相加的几何意义

改变坐标系当中点的坐标值。

矩阵相乘的几何意义

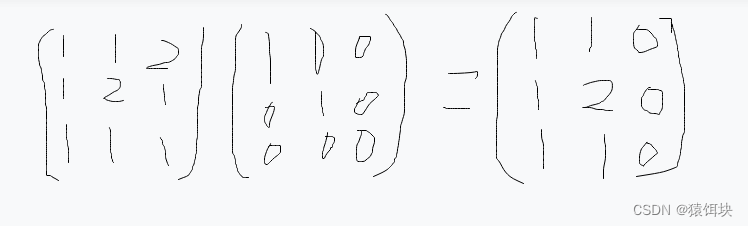
从图中可以看出，就是三维坐标中的三个点的坐标经过一个变换矩阵矩阵，变换成为这个坐标系内的另一个三个点的坐标。

所以矩阵相乘本质上就是改变点的坐标。

正交矩阵

旋转矩阵

只有旋转时：目标坐标系=基坐标系*旋转矩阵

目标坐标系的坐标是基于基坐标系的坐标旋转+移动得出的。

齐次变换矩阵在机器人中的作用

齐次变换矩阵的几何意义：

齐次变换矩阵用T来表示，是一个4*4的方正。

齐次变换矩阵包括从基坐标系到目标坐标系的旋转矩阵，以及基坐标系原点到目标坐标系原点的向量。

所以齐次坐标系的几何意义就是目标坐标系基于基坐标系旋转再移动所得的坐标系。

所以，如果点r基于目标坐标系的坐标为r1，基于基坐标系的坐标为r0，则点r的最终坐标为(基于全局坐标系，也就是基坐标系的坐标)：

r0=T*r1

T是基坐标系到目标坐标系的齐次变换(旋转+移动)，r1是基于目标坐标系的，不是基于基坐标系的，所以先通过T确定目标坐标系基于基坐标系的坐标，在T*r1才能得到r基于基坐标系的坐标。

为了配合齐次变换矩阵4*4的维度，点也用4维的行矩阵的转置或者列矩阵表示：

r={x,y,z,1}T

旋转矩阵和齐次变换矩阵看---《新版机器人技术手册》

世界坐标系--基坐标系

一个三维直角坐标系，以其为基准可以描述相机与待测物体的空间位置。

为什么要有世界坐标？
自己的理解：确定唯一且不变的世界坐标系之后，后面所有的坐标系都可以通过与世界坐标的相对关系来进行转换。此时，当我移动或者旋转世界坐标系的时候，通过相对关系可以很快速的得到其他坐标系下的数据。

机器人学（Robotics)

机械臂基础视频1

一些基础概念

刚体

刚性物体是一组粒子的集合，其中任意两个粒子之间的距离保持固定，不受物体运动或施加在物体上的力的影响。

“完全不可变形”的物体就是刚体。

?自由度

抽象定义：

物体能够对坐标系进行独立运动的数目称为自由度(Degree of Freedom，DOF)。

(就是能够对一个坐标系的所有坐标轴进行平移，旋转的数目)

机器人机构能够独立运动的关节数目，称为机器人机构的运动自由度，简称自由度。

位姿

位姿=位置+姿态

点的位置可用一个矢量(就是下面的列向量)来表示，物体的姿态可用一个矩阵(旋转矩阵)来表示。
?

位置

刚体的位姿即为刚体坐标系在基坐标系(世界坐标系)下的原点位置（位置），用一个向量来表示。

(就是用一个坐标系内的所有坐标轴表示一个点的坐标就是刚体内一个点的位置)

姿态

刚体运动坐标系的每一个坐标轴映射到世界坐标系对应坐标轴上所形成的向量(每一个向量由三个坐标值表示)，所以刚体运动坐标系的原点的姿态就需要三个向量，即3*3的矩阵表示。

姿态就是两个坐标系之间的旋转矩阵。

(就是机械臂末端执行器(就是机械臂的夹子)最终夹取物体的角度，是从上往下，还是从左往右，还是偏移。由?α?，β?，γ三个角度决定。)

链接

旋转矩阵描述姿态

目标坐标系B坐标系相对于基坐标系A的位姿描述：

R(上下标没加)是旋转矩阵，P(上下标没加)是目标坐标系的原点相对于基坐标系的位置矢量坐标。

位置+姿态=位姿

旋转矩阵+位置矢量=齐次变换矩阵

旋转矩阵有时候会被缩写为{n,o,a}，n,o,a是向量，表示原来三个点的坐标。

姿态的25种描述方法

1，旋转矩阵

2，欧拉角：

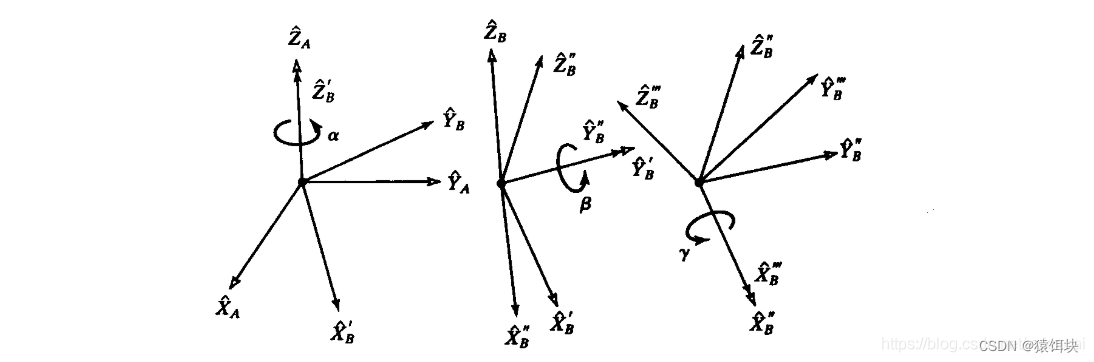
欧拉角的公式为何要将三个独立的旋转角相乘得到刚体的最终旋转矩阵？

因为从几何意义上就是先作相对于某一个轴的旋转，再作相对于某一个轴的旋转。

比如：R(α,β,γ)，就表示先作绕Z轴的旋转，再做绕Y轴的旋转，再做绕X轴的旋转。（注意轴和角的对应关系）

最终的旋转是每一个旋转相乘的最终组合。

欧拉角的绕旋转对象

欧拉角是绕着自身(目标坐标系)的轴旋转的，比如先绕Z轴旋转，旋转之后再绕Y轴旋转，之后再绕X轴旋转。

欧拉角有12种对姿态的描述方法---链接

3，固定角：

固定角是目标坐标系绕基坐标系的三个轴旋转进行的描述。

几何意义和欧拉角相同。

固定角也有12种对姿态的描述方法--链接

D-H变换矩阵：

四元数：

四元素的本质

如果你的English还可以，请看四元素讲解。

用于描述4维空间内的一个点的坐标，一个实部，三个虚部，虚部代表三个相互正交(垂直)的轴，也就是4维空间内的子空间三维空间的坐标轴。

q=w+xi+yj+zk;

i=j=k=-1;

也可以表示为：

q=((x,y,z,),w)=(v,w)

v是一个向量。

四元素是如何描述姿态的

等效轴角坐标系：

连杆

在理想状态下，忽略掉实际情况中的结构形变，我们可以将操作臂视为一系列刚体通过关节连接形成的一个运动链，我们将这些刚体称为连杆。

(关节)轴

关节轴就是关节所在的轴。

两个轴之间公垂线的长度就是两个关节轴之间连杆的长度。

机动度

柔性

即，机器人可编程。

操作点

操作者在机械臂上选择的一个点，通过这个点来秒速机械臂的运动。

运动学正解

所谓正运动学( direct kinematics),是指给出关节的位置、速度、加速度,求各个杆件的位置、姿态、速度、加速度、角速度﹑角加速度的问题。特别是求终端杆件(即末端执行器)的位置、姿态、速度、角速度的问题,这在应用上很重要。正运动学简称为DK。已知正运动学的解析法有齐次变换法和向量法。

目标坐标就是末端执行器要抓取的坐标点。

目标姿态就是末端执行器抓取时的角度。

末端

指末端执行器

法兰

动力学正解

动力学逆解

位置

速度

加速度

力矩

路径规划

机器人路径规划是规划的位置点

轨迹规划

轨迹规划是位置点+速度点+加速度点

机器人的基本组成

机器人感知系统

机器人的控制系统

机器人决策系统

机器人组成原理抠图

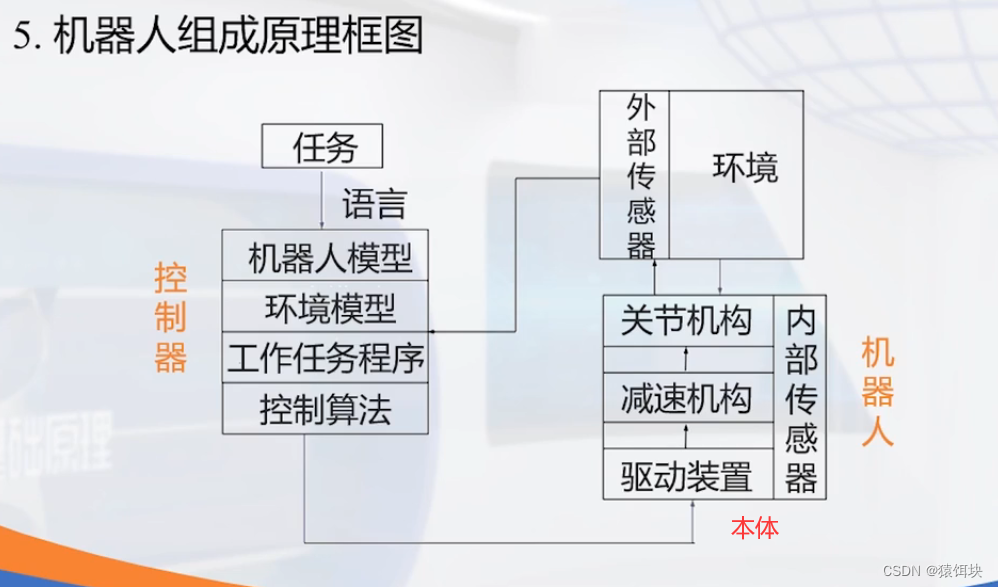
机器人的两种控制方式

机械臂的组成

机械臂正运动学

机械臂逆运动学

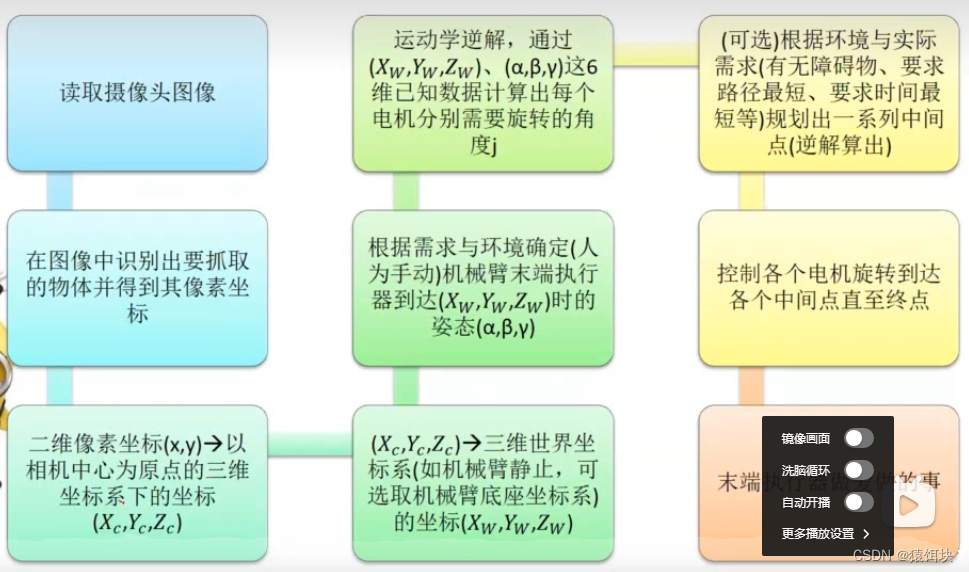
机械臂的抓取过程