【LSTM回归预测】基于贝叶斯优化多头注意力机制的卷积神经网络结合双向长短记忆网络BO-CNN-BiLSTM-Multihead-Attention实现数据回归预测附Matlab代码

【LSTM回归预测】基于贝叶斯优化多头注意力机制的卷积神经网络结合双向长短记忆网络BO-CNN-BiLSTM-Multihead-Attention实现数据回归预测附Matlab代码

文章介绍

BO-CNN-BiLSTM-Multihead-Attention是一种结合了贝叶斯优化、卷积神经网络（CNN）、双向长短记忆网络（BiLSTM）和多头注意力机制的模型，用于数据回归预测任务。该模型的目标是通过对输入数据进行处理和特征提取，以预测与输入数据相关的连续值输出。

模型的主要组成部分包括：

卷积神经网络（CNN）：CNN用于从输入数据中提取局部特征。它通过卷积层和池化层来捕捉输入数据中的空间结构信息，并将其转化为高级特征表示。

双向长短记忆网络（BiLSTM）：BiLSTM用于捕捉输入数据的时序依赖关系。通过在两个方向上运行LSTM单元，BiLSTM能够有效地捕捉到过去和未来的信息，从而更好地建模时间序列数据。

多头注意力机制：多头注意力机制用于聚合BiLSTM的输出，并捕捉输入数据中的全局关联性。通过引入多个注意力头，模型可以同时关注不同的特征子空间，并学习它们之间的相关性。

贝叶斯优化：贝叶斯优化用于优化模型的超参数。通过在参数空间中不断探索和评估不同的超参数组合，贝叶斯优化可以帮助找到最优的模型配置，以提高预测性能。

基于贝叶斯优化多头注意力机制的卷积神经网络结合长短记忆网络（BO-CNN-BiLSTM-Multihead-Attention）实现数据回归预测的优势包括以下几个方面：

1. 多模型结合：BO-CNN-BiLSTM-Multihead-Attention模型将卷积神经网络（CNN）、长短记忆网络（LSTM）和多头注意力机制结合在一起。CNN能够有效地提取输入数据的空间特征，LSTM能够建模时间序列数据的时序依赖关系，而多头注意力机制能够捕捉输入数据的全局关联性。通过综合利用这些模型的优势，BO-CNN-BiLSTM-Multihead-Attention模型能够更全面地建模输入数据，提高回归预测的准确性。
2. 贝叶斯优化超参数选择：贝叶斯优化方法能够自动地搜索和选择模型的超参数，从而找到最优的超参数组合。相比于传统的网格搜索或随机搜索，贝叶斯优化方法能够更高效地探索超参数空间，并在有限的试验次数内找到最优解。这有助于提高模型的性能和泛化能力。
3. 多头注意力机制：多头注意力机制能够同时关注不同的特征子空间，并学习它们之间的相关性。通过引入多个注意力头，模型能够更好地捕捉输入数据的全局关联性，从而提高回归预测的准确性。多头注意力机制还可以提供更丰富的特征表示，有助于模型更好地理解和解释输入数据。
4. 长短记忆网络（LSTM）的建模能力：LSTM能够有效地建模时间序列数据的时序依赖关系。对于回归预测任务，时序信息往往是重要的，而LSTM可以记忆和利用过去的信息，从而更好地预测未来的值。通过引入LSTM层，BO-CNN-BiLSTM-Multihead-Attention模型能够更好地应对具有时序特征的数据，提高回归预测的准确性。
5. 强大的泛化能力：BO-CNN-BiLSTM-Multihead-Attention模型在训练过程中通过使用训练集和验证集进行优化，并在测试集上进行评估，从而具备较强的泛化能力。它能够对未见过的数据进行准确的回归预测，适用于实际应用中的不同场景。

基于贝叶斯优化多头注意力机制的卷积神经网络结合长短记忆网络（BO-CNN-BiLSTM-Multihead-Attention）实现数据回归预测的缺点可能包括以下几个方面：

1. 模型复杂性：BO-CNN-BiLSTM-Multihead-Attention模型结构相对较复杂，包含了多个模型组件和多个超参数需要调整。这增加了模型的训练和调优的难度，需要更多的计算资源和时间。对于一些简单的回归预测任务，该复杂的模型结构可能过于庞大，不必要地增加了计算成本。
2. 训练和调参困难：BO-CNN-BiLSTM-Multihead-Attention模型的训练和调参相对复杂。贝叶斯优化方法虽然可以在有限次数的试验中搜索超参数空间，但仍需要进行多次模型训练和验证。这需要更多的时间和计算资源，而且对于非专业用户来说，可能需要一定的经验和专业知识来正确设置超参数和进行调优。
3. 模型解释性较弱：由于BO-CNN-BiLSTM-Multihead-Attention模型的复杂性，其内部的决策过程和特征权重分配可能相对难以解释。这对于某些应用场景来说可能不太理想，因为模型的解释性对于一些领域的决策制定者和用户是非常重要的。
4. 数据需求较高：BO-CNN-BiLSTM-Multihead-Attention模型通常需要大量的训练数据来充分发挥其优势。如果数据集较小或者数据质量较低，模型可能会过拟合或者无法捕捉到数据中的潜在特征和关联性。此外，模型中包含的多个模型组件和超参数也需要充足的数据来进行有效的训练和调优。
5. 可解释性与性能权衡：BO-CNN-BiLSTM-Multihead-Attention模型的复杂性可能会导致其解释性相对较弱。在某些应用场景中，模型的可解释性往往比性能指标更为重要。因此，在权衡解释性和预测性能之间时，需要根据具体的应用需求进行权衡和选择。

综上所述，基于贝叶斯优化多头注意力机制的卷积神经网络结合长短记忆网络（BO-CNN-BiLSTM-Multihead-Attention）实现数据回归预测的缺点主要包括模型复杂性、训练和调参困难、模型解释性较弱、对数据需求较高以及可解释性与性能权衡等方面。在应用该模型时，需要综合考虑这些因素，并根据具体情况进行评估和选择。

基本步骤

基于贝叶斯优化多头注意力机制的卷积神经网络结合长短记忆网络（BO-CNN-BiLSTM-Multihead-Attention）实现数据回归预测的基本步骤如下：

1. 数据准备：准备用于回归预测的训练集和测试集数据。确保数据集包含输入特征和对应的目标值。
2. 数据预处理：对输入数据进行必要的预处理，例如标准化、归一化或者其他特征处理方法，以便提高模型的训练效果。
3. 超参数选择：确定模型的超参数，包括卷积神经网络的层数、卷积核大小、池化层的大小、LSTM的隐藏单元数、注意力机制的头数等。这些超参数可以通过贝叶斯优化方法进行搜索和选择，以找到最优的超参数组合。
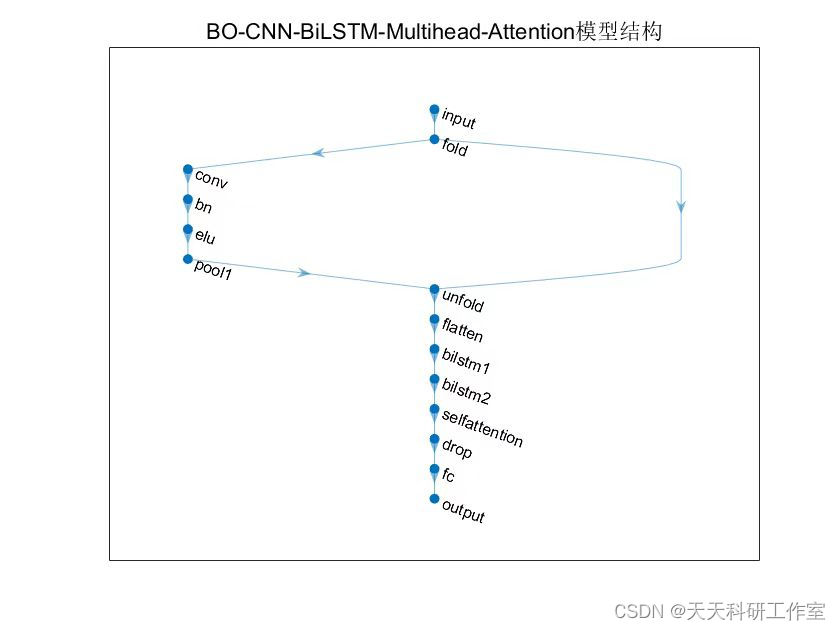
4. 模型构建：构建BO-CNN-BiLSTM-Multihead-Attention模型。模型的基本结构包括卷积神经网络层、BiLSTM层和多头注意力机制层。可以使用深度学习框架（如TensorFlow或PyTorch）来定义和搭建模型。
5. 模型训练：使用训练集对模型进行训练。通过反向传播算法和优化器（如随机梯度下降）来更新模型的参数，以最小化损失函数。可以选择合适的损失函数，如均方误差（Mean
   Squared Error，MSE）。
6. 超参数优化：使用贝叶斯优化方法对模型的超参数进行优化。贝叶斯优化可以自动地探索超参数空间，并找到最优的超参数组合。可以选择合适的贝叶斯优化库，如Bayesian
   Optimization and Hyperparameter Tuning (BOHB)或Optuna。
7. 模型验证：使用验证集评估模型的性能。计算回归任务的评估指标，如均方根误差（Root Mean Square
   Error，RMSE）或平均绝对误差（Mean Absolute Error，MAE），以衡量模型的预测精度。
8. 模型预测：使用训练好的模型对新的输入数据进行回归预测。将输入数据传递给模型，并获取模型的预测结果。
9. 模型评估：使用测试集评估模型在未见过的数据上的性能。计算回归任务的评估指标，如RMSE或MAE，以评估模型的泛化能力。

部分代码

%  数据集分析
outdim = 1;                                  % 最后一列为输出
num_size = 0.7;                              % 训练集占数据集比例
num_train_s = round(num_size * num_samples); % 训练集样本个数
f_ = size(res, 2) - outdim;                  % 输入特征维度

%%  划分训练集和测试集
P_train = res(1: num_train_s, 1: f_)';
T_train = res(1: num_train_s, f_ + 1: end)';
M = size(P_train, 2);

P_test = res(num_train_s + 1: end, 1: f_)';
T_test = res(num_train_s + 1: end, f_ + 1: end)';
N = size(P_test, 2);


%%  数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax('apply', P_test, ps_input);

[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);
%%  创建元胞或向量，长度为训练集大小；
XrTrain = cell(size(p_train,2),1);
YrTrain = zeros(size(t_train,2),1);
for i=1:size(p_train,2)
    XrTrain{i,1} = p_train(:,i);
    YrTrain(i,1) = t_train(:,i);
end
% 创建元胞或向量，长度为测试集大小；
XrTest = cell(size(p_test,2),1);
YrTest = zeros(size(t_test ,2),1);
for i=1:size(p_test,2)
    XrTest{i,1} = p_test(:,i);
    YrTest(i,1) = t_test (:,i);
end
%%  优化算法参数设置
%参数取值上界(学习率，隐藏层节点，正则化系数)
fitness = @fical;

%%  贝叶斯优化参数范围
optimVars = [
    optimizableVariable('NumOfUnits', [10, 50], 'Type', 'integer')
    optimizableVariable('InitialLearnRate', [1e-3, 1], 'Transform', 'log')
    optimizableVariable('L2Regularization', [1e-10, 1e-2], 'Transform', 'log')];

私信博主获取完整代码

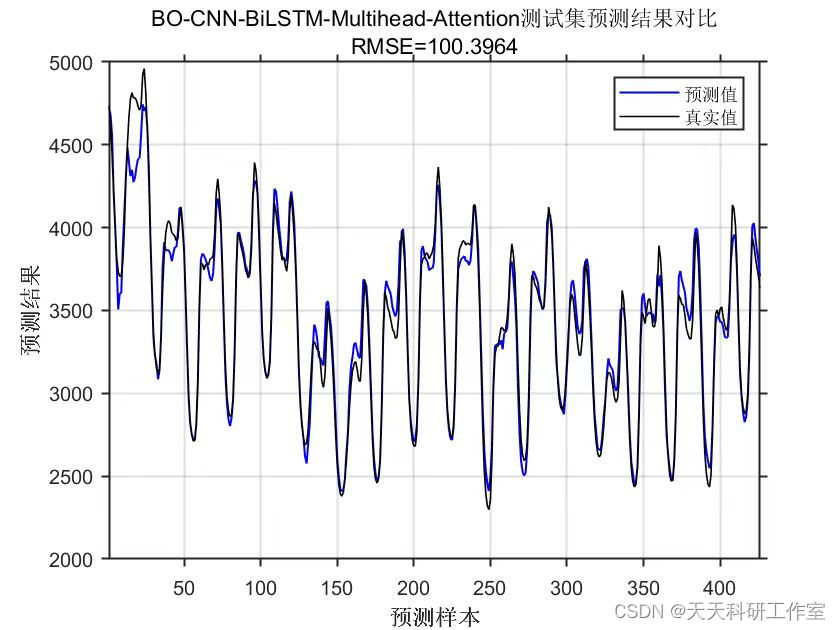
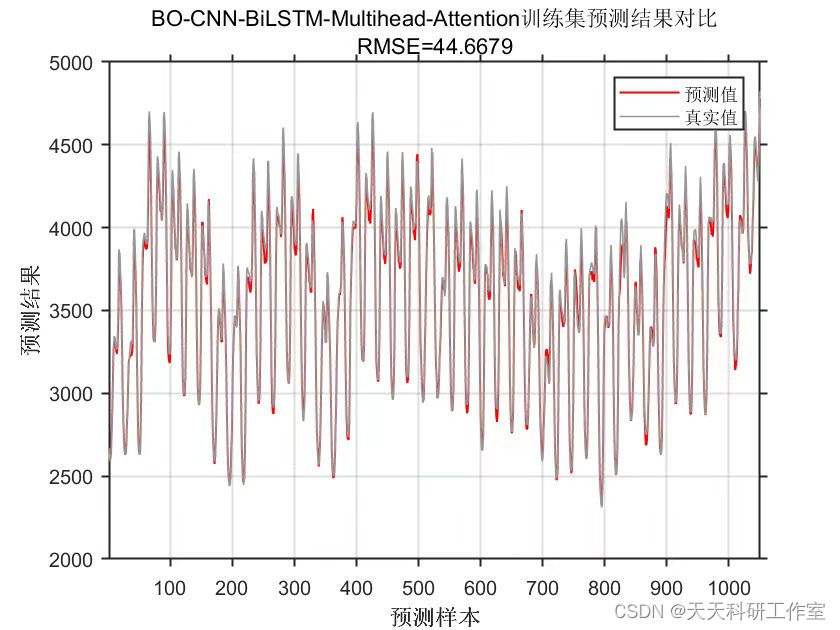
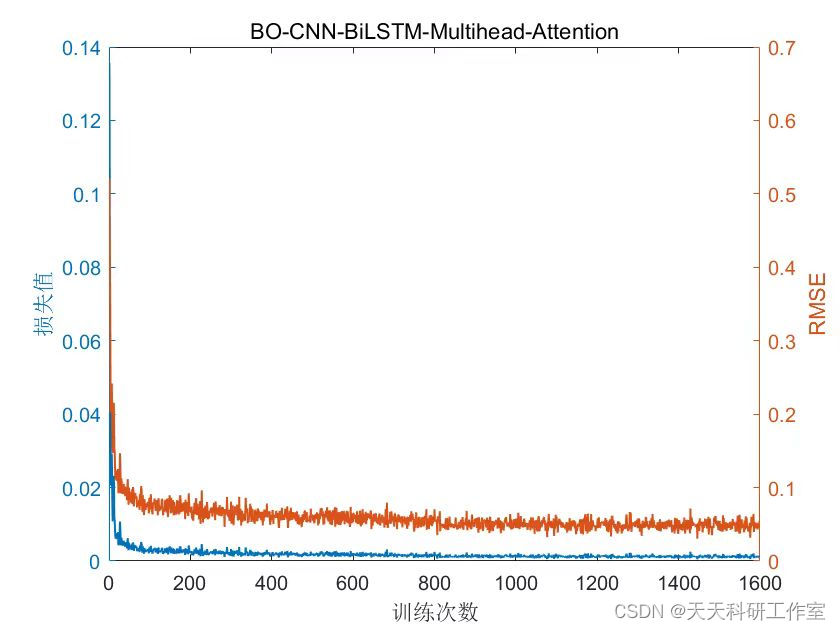
运行结果

参考资料

以下是一些与基于贝叶斯优化多头注意力机制的卷积神经网络结合双向长短记忆网络（BO-CNN-BiLSTM-Multihead-Attention）实现数据回归预测相关的参考资料，可以帮助你了解该方法的应用：

1.“AutoML for Neural Architecture Search: A Survey” - 这篇综述文章介绍了自动机器学习（AutoML）中的神经结构搜索（NAS）方法，其中包括贝叶斯优化和多头注意力机制的应用。你可以了解如何使用贝叶斯优化来优化神经网络结构。链接：https://arxiv.org/abs/1908.00709

2.“Convolutional LSTM Network: A Machine Learning Approach for Precipitation Nowcasting” - 这篇论文介绍了使用卷积神经网络结合长短记忆网络进行降水预测的方法，提供了一个使用卷积神经网络和LSTM结合的示例。链接：https://arxiv.org/abs/1506.04214

3.“Attention Is All You Need” - 这篇论文提出了Transformer模型中的注意力机制，它在自然语言处理任务中取得了显著的成果。你可以了解其中的多头注意力机制的原理和应用。链接：https://arxiv.org/abs/1706.03762

4.“A Bayesian Optimization Approach for Hyperparameter Tuning of Deep Neural Networks” - 这篇论文介绍了使用贝叶斯优化来调优深度神经网络超参数的方法。它可以帮助你了解如何在深度学习中应用贝叶斯优化。链接：https://arxiv.org/abs/1801.01271