批量归一化

2023-12-25 23:32:15

一、BN层介绍

1、深层神经网络存在的问题

2、批量归一化的解决方案

一、BN层介绍

???????批量归一化（Batch Normalization）是一种用于深度神经网络的常用技术，旨在加快模型的训练速度、提高模型的稳定性和泛化能力。

1、深层神经网络存在的问题

???????在深度神经网络中，反向传播算法用于计算网络参数的梯度，以便通过梯度下降等优化算法来更新参数。损失函数在神经网络的上层计算损失，梯度在反向传播过程中会逐层传递，通过链式法则计算每一层的梯度，就导致上层梯度大而下层梯度小。当网络层数很深时，梯度在传递过程中可能会变得非常小，甚至趋近于零，这就是梯度消失问题。

???????梯度消失问题会导致深层网络的参数难以更新，因为梯度信息无法有效地传播回浅层网络。这会导致浅层网络的参数在训练过程中几乎不会得到更新，从而影响了整个网络的训练效果。

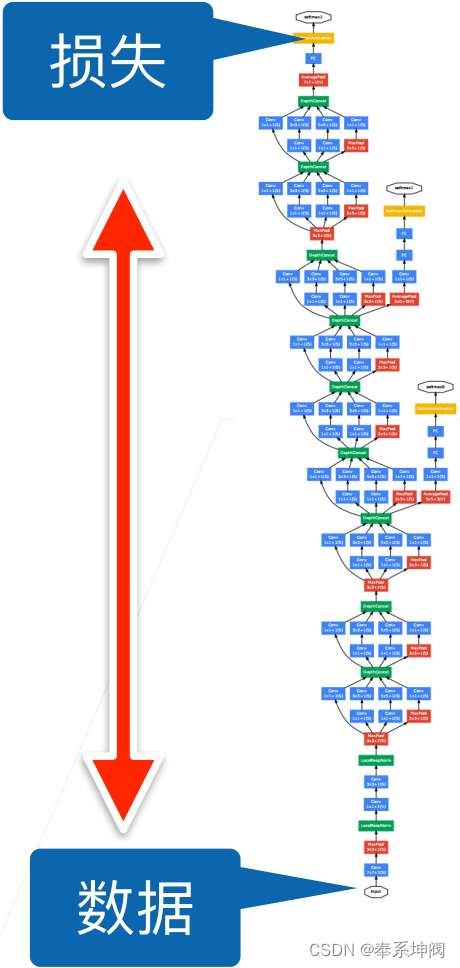
???????批量归一化的解决方案是在训练底层网络的时候避免顶部重新训练。

2、批量归一化的解决方案

? ? ? ?进行一个线性变换，学习一个新的 $\gamma$ 和 $\beta$ 使得数据变化不那么剧烈，对神经网络更友好。

???????因此 $x_i$ 的均值为 $\mu _B$ ，方差为 $\sigma _{B}^{2}$ 。

$Average\left( \frac{x_i-\mu _B}{\sigma _B} \right) =\mu _{B}^{'}=\frac{1}{\left| B \right|}\sum_{i\in B}{\frac{x_i-\mu _B}{\sigma _B}=}\frac{1}{\left| B \right|}\sum_{i\in B}{\frac{\left( x_1+x_2+...+x_B \right) -\mu _B\times B}{\sigma _B}=0}$

$Variance\left( \frac{x_i-\mu _B}{\sigma _B} \right) =\sigma _{B}^{'2}=\frac{1}{\left| B \right|}\sum_{i\in B}{\left( \frac{x_i-\mu _B}{\sigma _B}-\mu _{B}^{'} \right) ^2=}\frac{1}{\left| B \right|}\sum_{i\in B}{\left( \frac{x_i-\mu _B}{\sigma _B}-0 \right) ^2=\frac{1}{\left| B \right|}\sum_{i\in B}{\frac{\left( x_i-\mu _B \right) ^2}{\sigma _{B}^{2}}=}}\dfrac{\left( \frac{1}{\left| B \right|}\sum_{i\in B}{\left( x_i-\mu _B \right) ^2} \right)}{\sigma _{B}^{2}}=1$

???????因此 $\frac{x_i-\mu _B}{\sigma _B}$ 的均值为0，方差为1。

$Average\left( \gamma \frac{x_i-\mu _B}{\sigma _B}+\beta \right) =\mu _{B}^{''}=\frac{1}{\left| B \right|}\sum_{i\in B}{\left( \gamma \frac{x_i-\mu _B}{\sigma _B}+\beta \right) =\frac{\gamma}{\left| B \right|}\sum_{i\in B}{\frac{x_i-\mu _B}{\sigma _B}+\beta =\gamma \times \mu _{B}^{'}+\beta =\beta}}$

$Variance\left( \gamma \frac{x_i-\mu _B}{\sigma _B}+\beta \right) =\sigma _{B}^{''2}=\frac{1}{\left| B \right|}\sum_{i\in B}{\left( \gamma \frac{x_i-\mu _B}{\sigma _B}+\beta -\mu _{B}^{''} \right) ^2=\frac{\gamma ^2}{\left| B \right|}\sum_{i\in B}{\frac{\left( x_i-\mu _B \right) ^2}{\sigma _{B}^{2}}=\gamma ^2}}$

???????因此 $\gamma \frac{x_i-\mu _B}{\sigma _B}+\beta$ 的均值为 $\beta$ ，方差为 $\gamma ^2$ 。

样本减去其均值后除以方差的操作被称为标准化或归一化。这种操作常用于统计分析和机器学习中。

3、BN层作用位置

4、BN层加速模型训练的原因

???????批量归一化（Batch Normalization）在深度学习中能够加快模型训练速度的原因主要有以下几点：

???????缓解梯度消失问题：在深层神经网络中，梯度消失是一个常见的问题，导致较深层的梯度信息无法有效地传播回浅层网络。批量归一化通过对每一层的输入进行标准化，使得输入数据的均值接近0，方差接近1，从而使得激活函数的输入范围更加适中，避免了输入数据过大或过小，激活函数在其有效范围内具有较大的导数值，从而使得梯度能够更好地通过网络传播。这样，即使在深层网络中，梯度仍然可以有效地反向传播，从而保持参数的更新，缓解梯度消失问题，加速模型的训练过程。

???????加速收敛：批量归一化通过标准化每一层的输入，将数据分布调整为接近标准正态分布，使得网络的参数更容易学习。这有助于加快模型的收敛速度，减少训练的迭代次数，从而加速模型的训练过程。

???????增加学习率：批量归一化使得网络中的各层输入具有相对较小的变化范围，从而增加了模型对学习率的鲁棒性。较大的学习率可以加速模型的收敛，同时避免了因为学习率过大导致的不稳定性。

???????正则化效果：批量归一化本质上对每一层的输入进行了规范化处理，类似于一种正则化的效果。它在一定程度上减少了模型对输入数据的依赖，增强了模型的泛化能力，有助于防止过拟合。

???????总的来说，批量归一化通过标准化每一层的输入数据，缓解梯度消失问题，加快模型的收敛速度，增加学习率和正则化效果，从而有效地加快模型的训练速度。

5、总结

批量归一化固定小批量中的均值和方差，然后学习出适合的偏移和缩放
可以加速收敛速度，但一般不改变模型精度?

二、批量归一化从零实现

1、实现批量归一化操作

???????下面，我们从头开始实现一个具有张量的批量规范化层。

import torch
from torch import nn
from d2l import torch as d2l

def batch_norm(X, gamma, beta, moving_mean, moving_var, eps, momentum): # X:输入  gamma,beta:可学习参数γ,β  moving_mean,moving_var:全局均值和方差，做推理时用  eps:避免除0的东西  momentum:用来更新γ,β的参数
    # 通过is_grad_enabled来判断当前模式是训练模式还是预测模式
    if not torch.is_grad_enabled():
        # 如果是在预测模式下，直接使用传入的移动平均所得的均值和方差
        X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)
    else:
        assert len(X.shape) in (2, 4)   # 等于2的话就是全连接层，等于4的话就是卷积层
        if len(X.shape) == 2:
            # 使用全连接层的情况，计算特征维上的均值和方差
            mean = X.mean(dim=0)    # 二维的话第一维是批量大小(行)，第二维是特征(列)，dim=0表示每一列算出一个均值
            var = ((X - mean) ** 2).mean(dim=0)
        else:
            # 使用二维卷积层的情况，计算通道维上（axis=1）的均值和方差。
            # 这里我们需要保持X的形状以便后面可以做广播运算
            mean = X.mean(dim=(0, 2, 3), keepdim=True)
            var = ((X - mean) ** 2).mean(dim=(0, 2, 3), keepdim=True)
        # 训练模式下，用当前的均值和方差做标准化
        X_hat = (X - mean) / torch.sqrt(var + eps)
        # 更新移动平均的均值和方差
        moving_mean = momentum * moving_mean + (1.0 - momentum) * mean
        moving_var = momentum * moving_var + (1.0 - momentum) * var
    Y = gamma * X_hat + beta  # 缩放和移位
    return Y, moving_mean.data, moving_var.data

???????在全连接层中，输入数据的维度通常为两个，分别是：

批量大小（Batch Size）：表示一次输入的样本数量，即一批数据的大小。通常用于同时处理多个样本，以利用并行计算的优势。
特征维度（Feature Dimension）：表示每个样本在全连接层中的特征表示。这个维度的大小可以根据任务和网络设计进行调整，通常是通过将输入数据展平（flatten）为一维向量来实现。展平操作将多维的输入数据转换为一维的特征向量，作为全连接层的输入。

???????例如，如果输入数据的维度为[batch_size, num_features]，其中batch_size表示批量大小，num_features表示每个样本的特征维度，那么全连接层的两个维度就分别是batch_size和num_features。

2、创建BN层?

???????我们现在可以创建一个正确的`BatchNorm`层。这个层将保持适当的参数：拉伸`gamma`和偏移`beta`，这两个参数将在训练过程中更新。此外，我们的层将保存均值和方差的移动平均值，以便在模型预测期间随后使用。

???????撇开算法细节，注意我们实现层的基础设计模式。通常情况下，我们用一个单独的函数定义其数学原理，比如说`batch_norm`。然后，我们将此功能集成到一个自定义层中，其代码主要处理数据移动到训练设备（如GPU）、分配和初始化任何必需的变量、跟踪移动平均线（此处为均值和方差）等问题。为了方便起见，我们并不担心在这里自动推断输入形状，因此我们需要指定整个特征的数量。不用担心，深度学习框架中的批量规范化API将为我们解决上述问题，我们稍后将展示这一点。

class BatchNorm(nn.Module):
    # num_features：完全连接层的输出数量或卷积层的输出通道数。
    # num_dims：2表示完全连接层，4表示卷积层
    def __init__(self, num_features, num_dims):
        super().__init__()
        if num_dims == 2:
            shape = (1, num_features)
        else:
            shape = (1, num_features, 1, 1)
        # 参与求梯度和迭代的拉伸和偏移参数，分别初始化成1和0
        self.gamma = nn.Parameter(torch.ones(shape))
        self.beta = nn.Parameter(torch.zeros(shape))
        # 非模型参数的变量初始化为0和1
        self.moving_mean = torch.zeros(shape)
        self.moving_var = torch.ones(shape)

    def forward(self, X):
        # 如果X不在内存上，将moving_mean和moving_var
        # 复制到X所在显存上
        if self.moving_mean.device != X.device:
            self.moving_mean = self.moving_mean.to(X.device)
            self.moving_var = self.moving_var.to(X.device)
        # 保存更新过的moving_mean和moving_var
        Y, self.moving_mean, self.moving_var = batch_norm(
            X, self.gamma, self.beta, self.moving_mean,
            self.moving_var, eps=1e-5, momentum=0.9)
        return Y

???????在PyTorch中，nn.Parameter是一个特殊的张量，它被用作模型的可学习参数。当我们使用nn.Parameter包装一个张量时，PyTorch会自动将其标记为模型参数，使得在模型的训练过程中可以对其进行自动求导和更新。

???????在这段代码中，self.gamma和self.beta是可学习参数，它们用于缩放（gamma）和偏移（beta）归一化后的数据。因此，我们需要使用nn.Parameter将这两个张量标记为模型参数，以便可以对它们进行自动求导和更新。

???????而self.moving_mean和self.moving_var是批量归一化层中的非模型参数。它们用于保存移动平均的均值和方差，在训练过程中会被更新。但是它们不是模型的可学习参数，因此不需要使用nn.Parameter进行标记。

3、对LeNet加入批量归一化

???????为了更好理解如何应用`BatchNorm`，下面我们将其应用于LeNet模型。批量规范化是在卷积层或全连接层之后、相应的激活函数之前应用的。

net = nn.Sequential(
    nn.Conv2d(1, 6, kernel_size=5), BatchNorm(6, num_dims=4), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Conv2d(6, 16, kernel_size=5), BatchNorm(16, num_dims=4), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2), nn.Flatten(),
    nn.Linear(16*4*4, 120), BatchNorm(120, num_dims=2), nn.Sigmoid(),
    nn.Linear(120, 84), BatchNorm(84, num_dims=2), nn.Sigmoid(),
    nn.Linear(84, 10))

4、开始训练?

???????和以前一样，我们将在Fashion-MNIST数据集上训练网络。这个代码与我们第一次训练LeNet时几乎完全相同，主要区别在于学习率大得多。

lr, num_epochs, batch_size = 1.0, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

loss 0.273, train acc 0.899, test acc 0.807
32293.9 examples/sec on cuda:0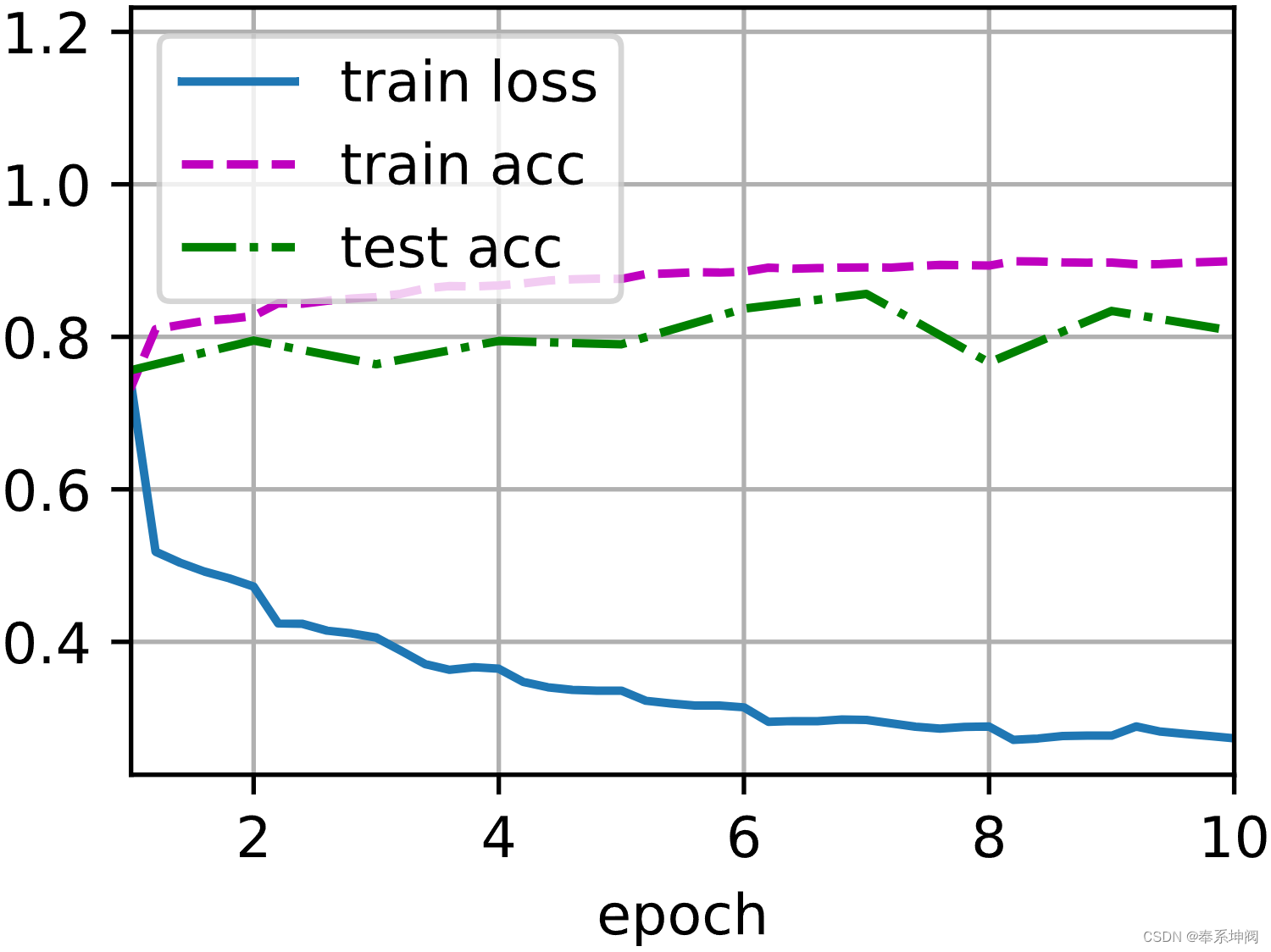

???????让我们来看看从第一个批量规范化层中学到的拉伸参数`gamma`和偏移参数`beta`。

net[1].gamma.reshape((-1,)), net[1].beta.reshape((-1,))

(tensor([0.4863, 2.8573, 2.3190, 4.3188, 3.8588, 1.7942], device='cuda:0',
        grad_fn=<ReshapeAliasBackward0>),
 tensor([-0.0124,  1.4839, -1.7753,  2.3564, -3.8801, -2.1589], device='cuda:0',
        grad_fn=<ReshapeAliasBackward0>))

三、简明实现

1、对LeNet加入批量归一化

???????除了使用我们刚刚定义的`BatchNorm`，我们也可以直接使用深度学习框架中定义的`BatchNorm`。该代码看起来几乎与我们上面的代码相同。

net = nn.Sequential(
    nn.Conv2d(1, 6, kernel_size=5), nn.BatchNorm2d(6), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Conv2d(6, 16, kernel_size=5), nn.BatchNorm2d(16), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2), nn.Flatten(),
    nn.Linear(256, 120), nn.BatchNorm1d(120), nn.Sigmoid(),
    nn.Linear(120, 84), nn.BatchNorm1d(84), nn.Sigmoid(),
    nn.Linear(84, 10))

2、开始训练?

???????下面，我们使用相同超参数来训练模型。通常高级API变体运行速度快得多，因为它的代码已编译为C++或CUDA，而我们的自定义代码由Python实现。

d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

loss 0.267, train acc 0.902, test acc 0.708
50597.3 examples/sec on cuda:0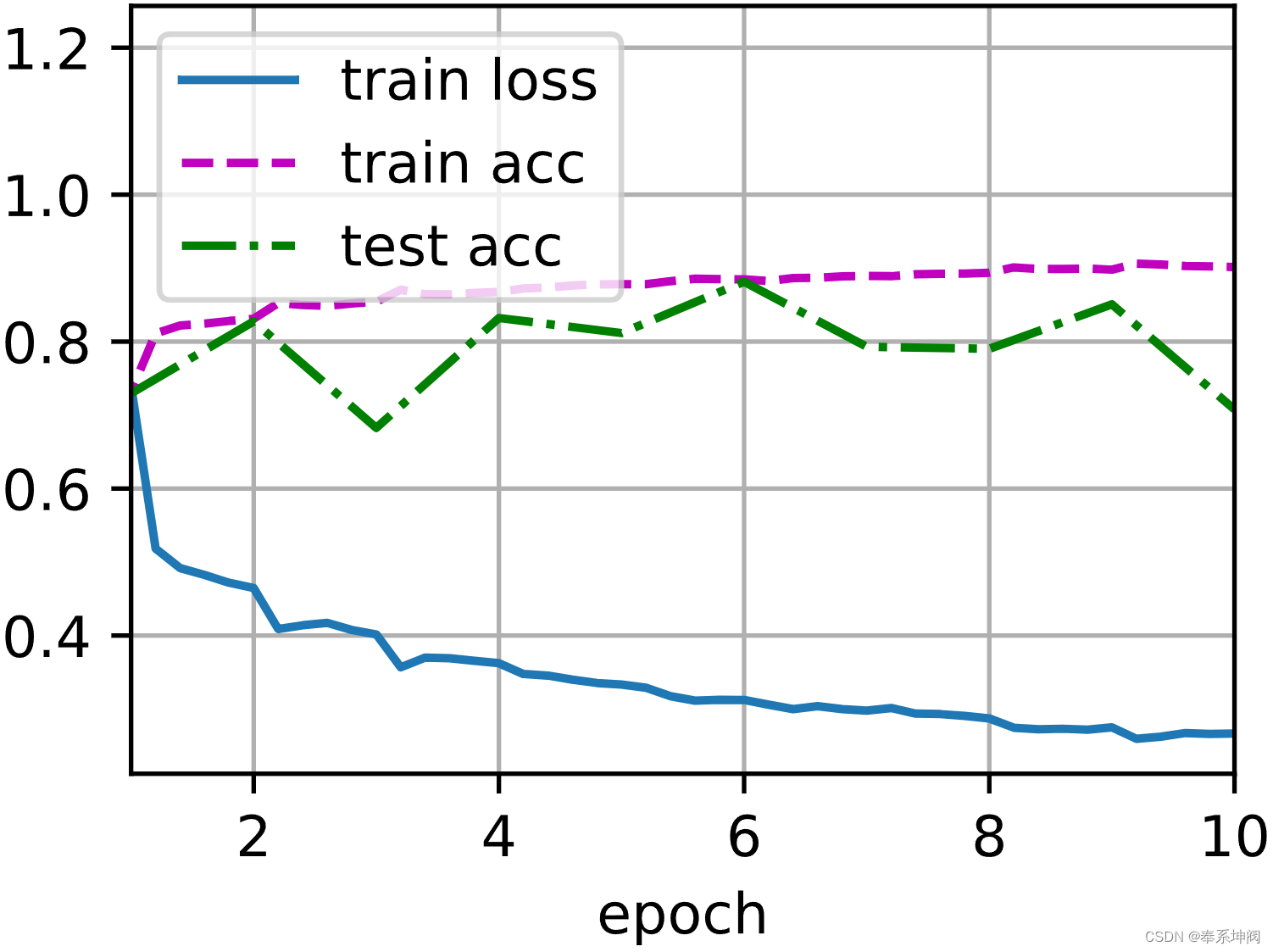

文章来源:https://blog.csdn.net/m0_56312629/article/details/135180513
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：veading@qq.com进行投诉反馈，一经查实，立即删除！