Dijkstra算法

目录

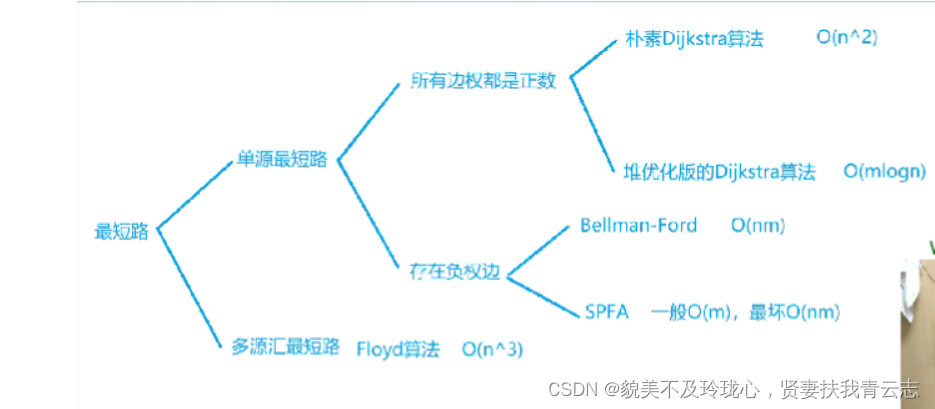
最短路问题

正边权-Dijkstra算法(朴素版)

正边权-Dijkstra算法（堆优化版）

---

最短路问题

最短路问题分类：

图论的问题难点在于从问题中找到对应的方法，难在分析处本质，这需要多做题，做过类似的，下次遇见才能做出来。所以要多做题，多分析。

稠密图用邻接矩阵存（二维数组），稀疏图用邻接表存

无向图是特殊的有向图，仅需要使用有向图的算法就可以解决无向图的算法。

正边权-Dijkstra算法(朴素版)

朴素Dijkstra用的是稠密图，用邻接矩阵存。

单源：仅有一个起点。

板子

int g[N][N];  // 存储每条边
int dist[N];  // 存储1号点到每个点的最短距离
bool st[N];   // 存储每个点的最短路是否已经确定

// 求1号点到n号点的最短路，如果不存在则返回-1
int dijkstra()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;

    for (int i = 0; i < n - 1; i ++ )
    {
        int t = -1;     // 在还未确定最短路的点中，寻找距离最小的点
        for (int j = 1; j <= n; j ++ )
            if (!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;

        // 用t更新其他点的距离
        for (int j = 1; j <= n; j ++ )
            dist[j] = min(dist[j], dist[t] + g[t][j]);

        st[t] = true;
    }

    if (dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

思路：基于贪心策略,只能解决正边权的问题。

代码逻辑
for(遍历所有的点)
{
	for(遍历所有点)
		if(点未被确定最短距离 && 点距离起点最近)
		t=j;
	
	st[t]=true; //点被放入集合
	
	for(遍历所有的点)
	{
		d[j]>d[t]+g[t][j] 就更新d[j];
	}
	
}

解题代码

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 510;

int n, m;
int g[N][N];
int dist[N];
bool st[N];

//g[3][4]=7  存储3节点到4节点的距离为7
//dist数组存储到初始点的距离 
//state记录当前的点是否找到了距离初始点的最短距离 

int dijkstra()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
	//循环n次，遍历所有的点 
    for (int i = 0; i < n - 1; i ++ )
    {
    	//用t记录即将筛选到还没确定状态的最近的点
		//这一层循环的作用是找到那个最近的点，修改状态，列入以确定的点 
		//这个点的充分条件是未被纳已经搜到的范围且它的距离是到初始点最小的。
        int t = -1;
        for (int j = 1; j <= n; j ++ )
            if (!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;
		
		//用刚列入的点取更新与它相连接的边
		//这个过程实际上为之后找点埋下伏笔 
        for (int j = 1; j <= n; j ++ )
            dist[j] = min(dist[j], dist[t] + g[t][j]);

        st[t] = true;
    }

    if (dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

int main()
{
    scanf("%d%d", &n, &m);

    memset(g, 0x3f, sizeof g);
    while (m -- )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);

        g[a][b] = min(g[a][b], c);
    }

    printf("%d\n", dijkstra());

    return 0;
}

思路：

1. 遍历n-1次控制，遍历所有的点，最后的点不需要再遍历了

2. 找出距离最近的点，纳入已经确定最短距离的点，更新状态

3. 用新找到的点取更新与它相连的边

4. 第三步为之后的第二再次埋下伏笔

正边权-Dijkstra算法（堆优化版）

板子：

这种算法是基于一种贪心得策略，每次用这个点得最短距离去更新与它想连接得所有点，所得最小得距离得那个点就是最小得点。

举个栗子：有三个点与初始点有边，dist中最小得点就可以被确定为已经有最小距离得点，因为，dist[j]<dist[other node]+dist [other node] [j] 恒成立，所以这种贪心得策略是完全没问题得，具体得充分证明可以参考网上。

typedef pair<int, int> PII;

int n;      // 点的数量
int h[N], w[N], e[N], ne[N], idx;       // 邻接表存储所有边
int dist[N];        // 存储所有点到1号点的距离
bool st[N];     // 存储每个点的最短距离是否已确定

// 求1号点到n号点的最短距离，如果不存在，则返回-1
int dijkstra()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    priority_queue<PII, vector<PII>, greater<PII>> heap;
    heap.push({0, 1});      // first存储距离，second存储节点编号

    while (heap.size())
    {
        auto t = heap.top();
        heap.pop();

        int ver = t.second, distance = t.first;

        if (st[ver]) continue;
        st[ver] = true;

        for (int i = h[ver]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (dist[j] > distance + w[i])
            {
                dist[j] = distance + w[i];
                heap.push({dist[j], j});
            }
        }
    }

    if (dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

思路：

1. 遍历优先队列，优先队列得第一个点就是可以确定已有最小距离得点，具体得原因是和边更新距离得贪心策略有关，绝对充分

2. 遍历所有与这个点有边得所有其他点，用队列得第一个点得距离更新与它相连得其他所有点得最小距离

3. 这个过程中每个点得pair只会再队列中存在一次的，把更新距离得点放进优先队列中

重复1，2，3，得过程 当队列为空时，就完成对所有点得最小距离得确定

堆优化的优点是堆与稀疏图，也就是边少的图，使用边更新最小距离可以有效降低时间复杂度

if (st[ver]) continue;
st[ver] = true;

放进队列的点不一定全部会在遍历图中全部使用到，如果最后一个点的最小距离也被遍历到后，也可能美哟使用到，所以这是我们需要使用这段代码把它从队列中踢出去

auto t = heap.top();
        heap.pop();

st[ver] = true;

?把队列中未使用到的数据给踢出去，结束队列；if

解题代码

#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>

using namespace std;

typedef pair<int, int> PII;

const int N = 1e6 + 10;

int n, m;
int h[N], w[N], e[N], ne[N], idx;//存储稀疏图 
int dist[N];//记录每个点到初始点得距离 
bool st[N];//记录点得状态是否被确定最小距离 

//稠密图是点少，边多
//系数图是点多，边少
//这是相对而言 

//邻接表存储稀疏图 
void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

//优化版的dijkstra是 
int dijkstra()
{
	//初始化dist数组为无限大 
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    //priority_queue<参数一：数据类型（pair）,参数二：STL类型（vector）,排序类型：(greater)从小到大，(less)从大到小> 
    priority_queue< PII, vector<PII>, greater<PII> > heap;
    heap.push({0, 1});//第一个是距离，第二个是点，queue得排序第一优先规则是距离 
	
	//只要prioruty_queue不空，就一直取元素 
    while (heap.size())
    {
        auto t = heap.top();
        heap.pop();
		
        int ver = t.second, distance = t.first;
		 
		//ver这个点只要未被确定最短距离，就取出来，修改状态 
        if (st[ver]) continue; 
        st[ver] = true; 
		//遍历与ver这个点想连得所有点，用ver得距离取修改与它相连得所有点得最小距离 
        for (int i = h[ver]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (dist[j] > dist[ver] + w[i]) 
            {
                dist[j] = dist[ver] + w[i];
                heap.push({dist[j], j}); 
            }
        }
    }

    if (dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

int main()
{
    scanf("%d%d", &n, &m);

    memset(h, -1, sizeof h);
    while (m -- )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);
    }

    cout << dijkstra() << endl;

    return 0;

}