高级算法设计与分析（七） -- 概率算法和NP完全性理论

系列文章目录

高级算法设计与分析（一） -- 算法引论

高级算法设计与分析（二） -- 递归与分治策略

高级算法设计与分析（三） -- 动态规划

高级算法设计与分析（四） -- 贪心算法

高级算法设计与分析（五） -- 回溯法

高级算法设计与分析（六） -- 分支限界法

高级算法设计与分析（七） -- 概率算法和NP完全性理论

高级算法设计与分析（八） -- 总结

---

目录

系列文章目录

前言

一、概率算法

1、随机数

2、数值概率算法

3、***Las Vegas算法(拉斯维加斯)

二、NP完全性理论

1、P类与NP类问题

2、NP完全问题

3、一些典型的NP完全问题

4、另一种描述

1.1、NP完全性理论

1.2、P问题

1.3、NP问题

1.4、NP完全问题（NPC（complete））

1.5、NP难问题（NP-hard）

1.6、P、NP、NPC、NP难问题的关系

---

前言

tips：这里只是总结，不是教程哈。鉴于本人写字如画符，就不出视频教程了，如实在有需要，请在文章下方留言。当然，文章有任何问题，也请留言，谢谢！

这个系列用另一种形式，把习题放在最下面，看看好用不。

本系列文章最后一文会进行简要全部总结，以及思维导图放在最后一篇文章最下面，请自行获取。

---

一、概率算法

1、随机数

?

?

?

2、数值概率算法

?

?

3、***Las Vegas算法(拉斯维加斯)

?

二、NP完全性理论

1、P类与NP类问题

?

?

?

?

2、NP完全问题

?

?

?

?

?

3、一些典型的NP完全问题

?

4、另一种描述

1.1、NP完全性理论

?

1.2、P问题

一类能够用确定的算法在多项式时间内求解的可判定问题（也称为多项式类型）

????????确定的算法：与之相反的算法叫随机化算法。
????????????????给定一个问题用这个算法去解决，得到的结果是唯一的。
????????????????用随机化算法，同样的输入每一次运行的结果可能不同。

????????可判定问题

1.3、NP问题

一类能够用不确定的算法在多项式时间内求解的可判定问题

????????1、“猜”
????????2、猜出一个解来，在多项式时间以内，可以验证这个问题的正确性。

1.4、NP完全问题（NPC（complete））

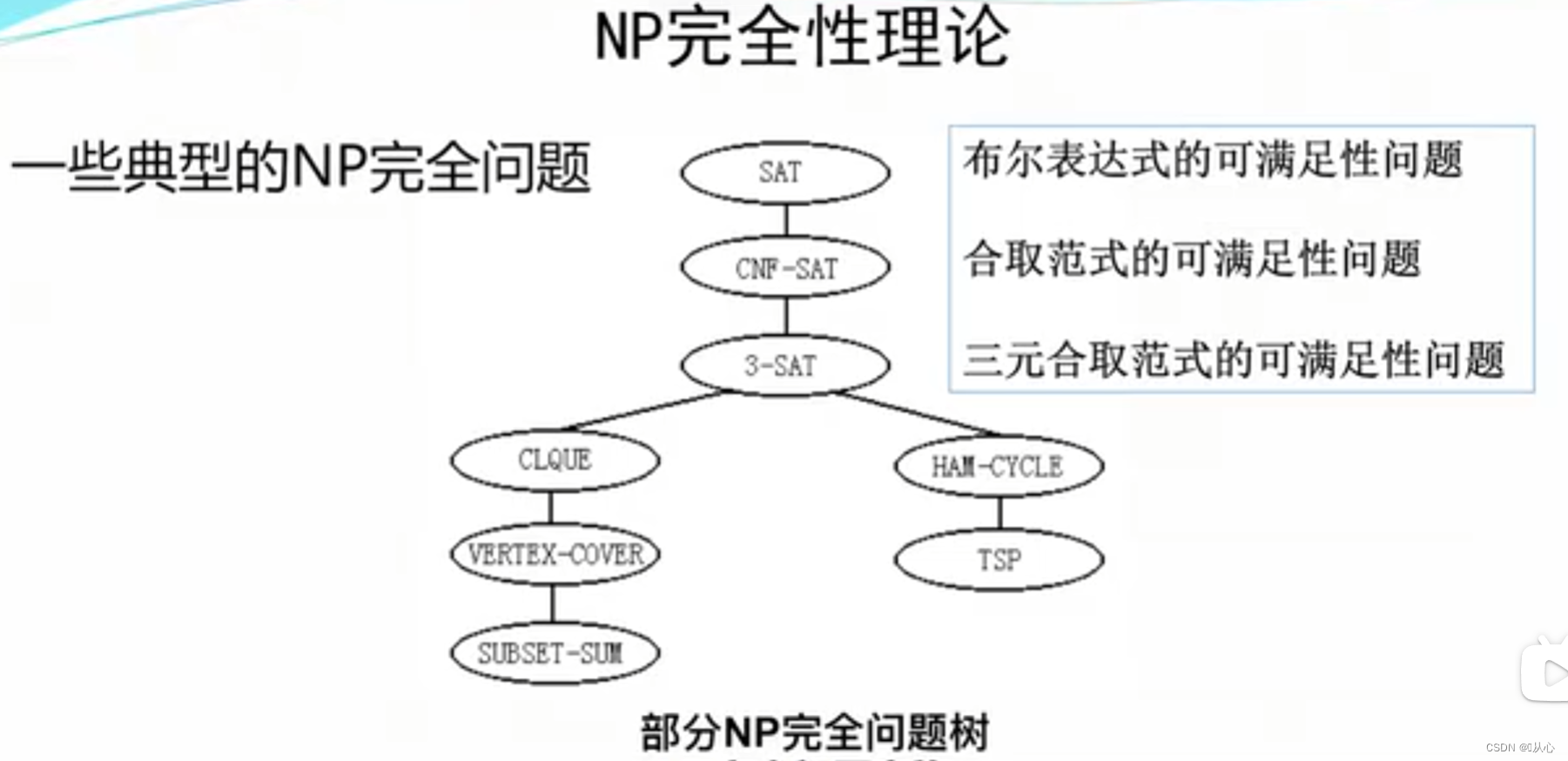
1.5、NP难问题（NP-hard）

NP难问题满足NPC问题的性质2，不一定满足性质1；
NPC=NP交集NP难

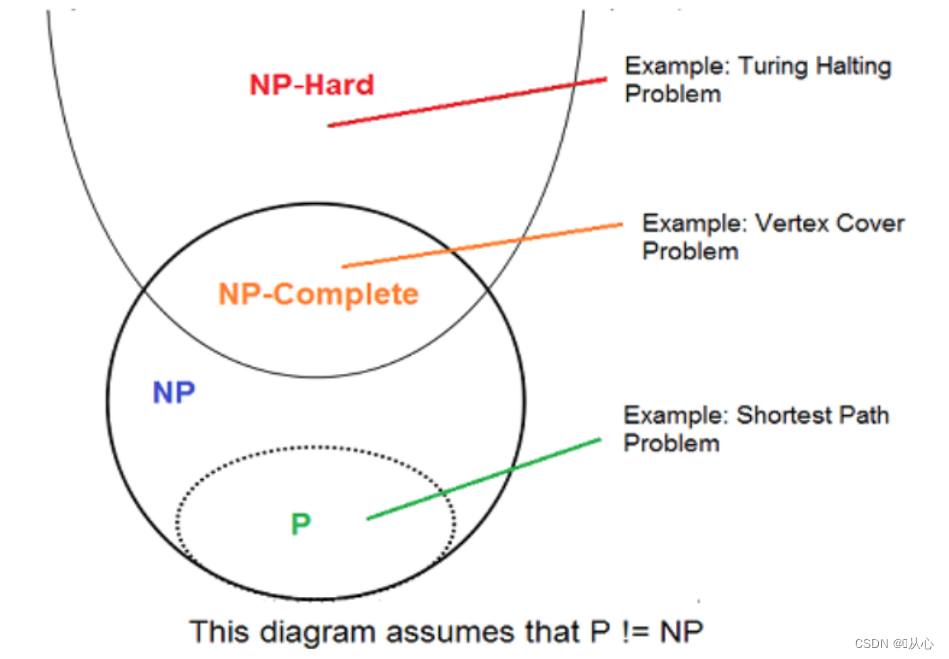
1.6、P、NP、NPC、NP难问题的关系

P=NP意味着NP当中的所有问题都能有确定性算法，在多项式时间之内解决