关于B+树的总结

B树(B-tree)

B树属于多叉树又名平衡多路查找树（查找路径不只两个），数据库索引技术里大量使用着B树和B+树的数据结构

• 规则：

（1）排序方式：所有节点关键字是按递增次序排列，并遵循左小右大原则；

（2）子节点数：非叶节点的子节点数>1，且<=M ，且M>=2，空树除外（注：M阶代表一个树节点最多有多少个查找路径，M=M路,当M=2则是2叉树,M=3则是3叉）；

（3）关键字数：枝节点的关键字数量大于等于ceil(m/2)-1个且小于等于M-1个（注：ceil()表示向上取整?如ceil(1.1)结果为2);

（4）所有叶子节点均在同一层、叶子节点除了包含了关键字和关键字记录的指针外也有指向其子节点的指针只不过其指针地址都为null对应下图最后一层节点的空格子;

B+树

• 规则

1. 每一个父节点的元素都出现在子节点中，是子节点的最大（最小）元素，因此根节点的最大元素也是整个B+树的最大元素。

（2）每一个叶子结点都带有指向下个节点的指针，形成了一个有序链表。

（3）只有叶子结点有其索引指向的数据记录，中间节点仅是索引。

B+树的特征：

1.有k个子树的中间节点包含有k个元素（B树中是k-1个元素），每个元素不保存数据，只用来索引，所有数据都保存在叶子节点。

2.所有的叶子结点中包含了全部元素的信息，及指向含这些元素记录的指针，且叶子结点本身依关键字的大小自小而大顺序链接。（链表）

3.所有的中间节点元素都同时存在于子节点，在子节点元素中是最大（或最小）元素。

4、B+树查找时是从上到下查找；B-树则是从下往上查找（中序遍历）

B+树的优势：

1.单一节点存储更多的元素（这样该节点下分支变多了，树变矮胖了），使得查询的IO次数更少。

2.所有查询都要查找到叶子节点，查询性能稳定。

3.所有叶子节点形成有序链表，便于范围查询。

ASL平均查找长度：

设关键字个数为n,在各关键字等概率查找的前提下,
1、顺序查找的平均查找长度ASL=(n+1)/2,
2、在n趋于无穷大时,折半查找的ASL=((n+1)log2(n+1))/n - 1,当n大于50时,ASL约等于log2(n+1)-1
3、设分块查找中将长为 n 的表分成均等的 b 个块,每块 s 个元素,则 b = (n / s)上取整,如果索引表中采用顺序查找,则ASL=(b+1)/2+(s+1)/2；如果索引表中采用折半查找,则ASL=(s+1)/2+log2(b+1)-1

折半查找：

例：给11个数据元素有序表（2,3,10,15,20,25,28,29,30,35,40）采用折半查找。则ASL成功和不成功分别是多少？

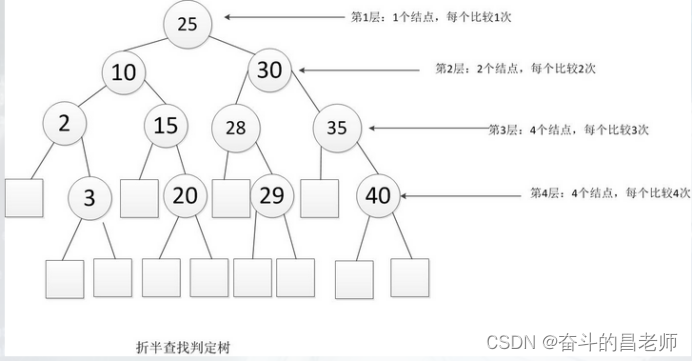
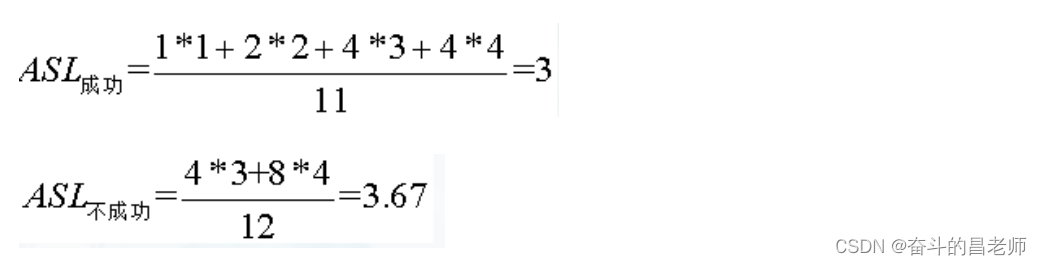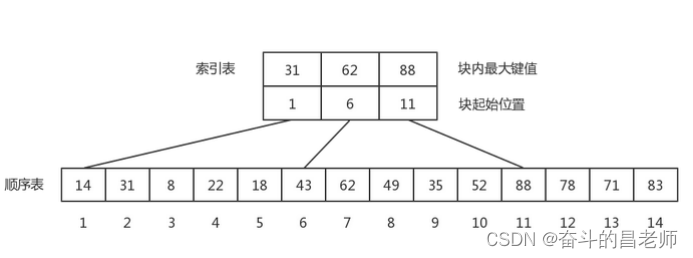
分块查找：

分块查找又称索引顺序查找，它是顺序查找的一种改进方法。

　　算法流程：

• 先选取各块中的最大关键字构成一个索引表；
• 查找分两个部分：先对索引表进行二分查找或顺序查找，以确定待查记录在哪一块中；然后，在已确定的块中用顺序法进行查找。