数学建模算法
算法部分
算法讲解
matlab代码大全
1. 评价类模型




2. TOPSIS
构造计算评分的公式: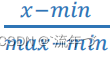
topsis评价模型:将原始数据矩阵统一指标类型(一般正向化处理) 得到正向化的矩阵
代码
3. 线性规划
-
线性规划(linprog)模型:高中知识所学
-
整数线性规划(intlinprog)模型:变量有部分限制为整数的线性规划
-
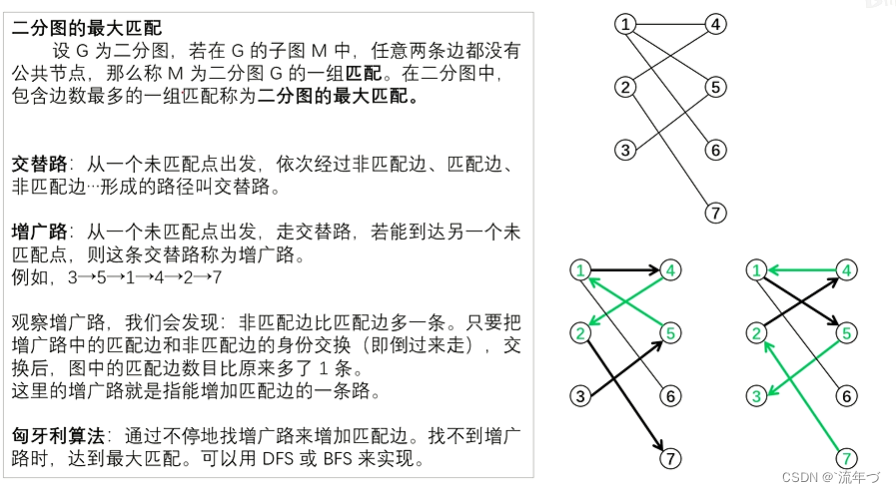
匈牙利算法:求解任务分配问题的组合优化算法(一对一的问题)
二分图最大匹配 匈牙利算法:用于寻找最大匹配,通过不断寻找怎光路径,来寻找最大匹配问题
讲解传送
- 非线性规划(fmincon)模型:目标函数或者约束条件中包含非线性函数
非线性规划例题传送阵 - 二次规划(quadprog)模型:目标函数自变量为x的二次函数约束条件又全是线性的
- 多目标规划(fgoalattain)模型:研究多于一个的目标函数在给定区域上的最优化,给予权重来评判目标重要性
matlab代码传送阵 - 绘制柱形竞赛图:https://blog.csdn.net/zhwzhaowei/article/details/110915135
4. 聚类分析
聚类分析(pdist)是根据在数据中发现的描述对象及其关系的信息,将数据对象分组。目的是,组内的对象相互之间是相似的(相关的),而不同组中的对象是不同的(不相关的)。
组内相似性越大,组间差距越大,说明聚类效果越好
K-Means聚类算法代码通道
X=[0 0;1 0;0 1;1 1;2 1;1 2;2 2;3 2;6 6;7 6;8 6;6 7;7 7;8 7;9 7;7 8;8 8;9 8;8 9;9 9]; % X:N*P的数据矩阵
[idx,C,sumd,d] = kmeans(X,2); % idx:N*1的向量,存储的是每个点的聚类标号
figure; % K = 2;表示将X划分为几类,为整数。 C:K*P的矩阵,存储的是K个聚类质心位置
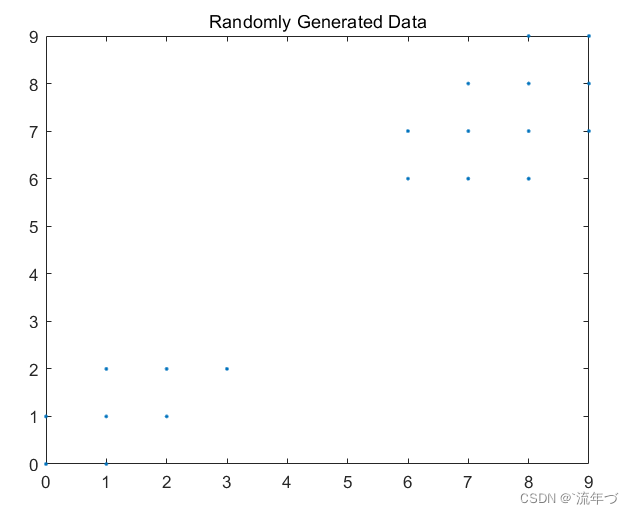
plot(X(:,1),X(:,2),'.'); % sumd:1*K的和向量,存储的是类间所有点与该类质心点距离之和。 d:N*K的矩阵,存储的是每个点与所有质心的距离
title 'Randomly Generated Data';
figure;
plot(X(idx==1,1),X(idx==1,2),'r.','MarkerSize',12)
hold on
plot(X(idx==2,1),X(idx==2,2),'b.','MarkerSize',12)
plot(C(:,1),C(:,2),'kx',...
'MarkerSize',15,'LineWidth',3)
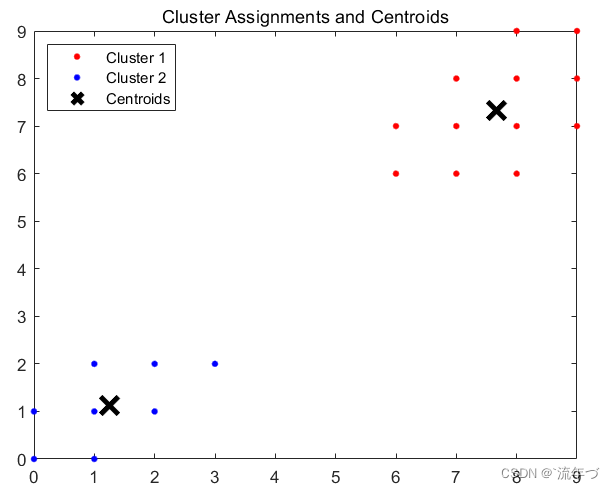
legend('Cluster 1','Cluster 2','Centroids',...
'Location','NW')
title 'Cluster Assignments and Centroids'
hold off
5. 预测模型
- 灰色预测模型:对原始数据进行生成处理来寻找系统变动的规律,并生成有较强规律性的数据序列,然后建立相应的微分方程模型,从而预测事物未来发展趋势的状况。
最小二乘法代码传送 ????????矩阵基本法使用与代码讲解 - 时间序列预测模型:按照时间顺序,一定的时间间隔取得的一系列观测值,进而预测以后的数据
时间序列分析传送阵??时间序列例题及代码分析 - 模拟退火优化算法1
模拟退火优化算法2
6. 拉伊达准则(对异常值进行剔除)
??????假设一组检测数据只含有随机误差,对其进行计算处理得到标准偏差,按一定概率确定一个区间,认为凡超过这个区间的误差,就不属于随机误差而是粗大误差,含有该误差的数据应予以剔除,基于3σ原则
代码实现传送阵????正太检验
7. 数据拟合
8. 图论
握手定理
- 在任何有向图图中,所有顶点的度数之和等于边数的2倍,所有顶点的入度之和等于所有顶点出度之和,等于边数
- 无向简单图,同样所有顶点的度数之和等于边数的2倍
有限简单图
-
顶点个数有限
-
任意一条边有且只有两个不同的点与它相互关联
-
边之间不能够重复
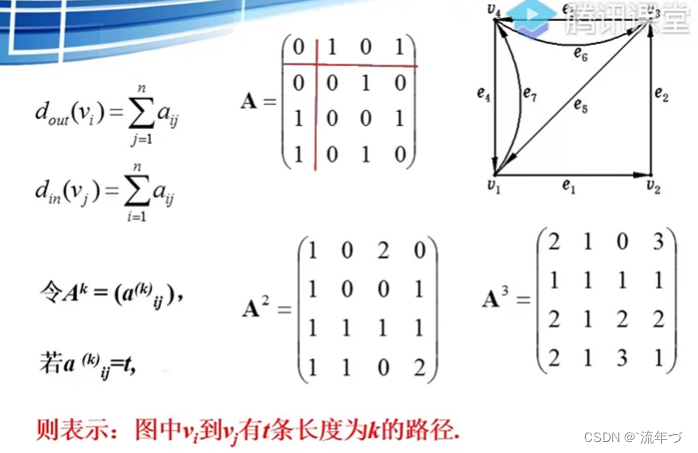 矩阵的表示PPt
矩阵的表示PPt -
Dijkstra讲解:求最短路径问题
Dijkstra算法matlab传送阵1
Dijkstra算法matlab传送阵2 -
kruskal:连通网中查找最小生成树
讲解视频
kruskal matlab传送阵 -
神经网络:实现分类与预测模型
Bp神经预测代码传送
Bp神经分类代码传送
匹配讲解:在一个图中,两个不相邻的边,称之为匹配;其边上的两个端点称之为配对的;若匹配集M的某条边与顶点v是关联的,则称M饱和顶点v
代码练习
1. 模拟圆周率
allPoints = input("请输入总点数:")
count = 0
for i = 1:allPoints
if rand^2 + rand^2 <=1
count = count + 1
end
end
res = count / allPoints * 4
disp(res)
2. 斐波那契数列
N = input("请输入项数:")
res = [1,1]
for i = 3:N
element = res(length(res)) + res(length(res) - 1)
res = [res,element]
disp(res)
3. 四只鸭子落在一个圆中概率
N = 4
count = 0
total =1000 %试验次数
for i = 1:total
p1 = 2*[rand,rand]-1;
p2 = 2*[rand,rand]-1;
p3 = 2*[rand,rand]-1;
p4 = 2*[rand,rand]-1;
p = [p1,p2,p3,p4]; %生成4 2 矩阵
for j = 1:N
k = p(i,2) / p(i,1);
b = [];
if (i == j)
continue;
else
b = [b, p(i,2) - p(i,1)*k];
end
end
end
if (b(1)>=0 & b(2)>=0 & b(3)>=0 | b(1)<=0 & b(2)<=0 & b(3)<=0)
count = count + 1;
res = count/total;
disp(res);
# 拓展N只鸭子
% 生成N个随机点
function p Npoints(N)
p = [];
for i = 1:N
p = [p;2*[rand,rand]-1] % 每一列
end
end
% 判断截距的一致性
function isEqual ifisEqual(b)
isEqual = 1;
if b(1)>=0
for i = 1:length(b)
if b(i)<0
isEqual = 0;
end
end
else
for i = 1:length(b)
if b(i)>0
isEqual = 0;
end
end
end
end
4. 方程2: y" = uy’ + y,初值y(0) = 1,y(0) =0
syms y(x) mu
eqn = diff(y,2) == mu*diff(y)+y;
cond1 = y(0) == 1;
Dy(0) == 0;
dsolve(eqn) % dsolve(方程,初值) 常微分方程求解
B = repmat(A,m, n):将矩阵A复制m×n块,即把A作为B的元素,Btm×n个A平铺而成。
prod():与sunm类似,求积
数据导入函数:weitetable()
数据导出函数:readtable()
Y = round(X,N,type) 指定四舍五入的类型
type filename 在 MATLAB 命令行窗口中显示指定文件的内容
imread(x.jpg):图片读入,以(0:255)读入,格式为 unit8
imshow(x)矩阵图片显示
imresize(x,0.5)图片大小更改
imwrite(x.jpg):图片写入,以图片存入路径
imbinarize(a):将图片矩阵二值化
logical(A):将矩阵A转换为逻辑值(即非零即为1)
bwlabel(A,4/8):联通分量化
solve(方程1,方程2…,变量1,变量2…):求解函数
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
