【论文笔记】DSVT: Dynamic Sparse Voxel Transformer with Rotated Sets

原文链接：https://arxiv.org/abs/2301.06051

1. 引言

本文提出DSVT，一种通用的、部署友好的、基于transformer的3D主干，可用于多种基于点云处理的3D感知任务中。

传统的稀疏点云特征提取方法，如PointNet系列和稀疏卷积，要么需要高计算力进行采样与分组，要么因为子流形卷积导致表达能力受限。且这些方法需要自己编写CUDA程序，无法利用现成的深度学习工具如PyTorch。基于Transformer的方法会因为大量的空体素而引入额外计算，一些改进要么会降低性能，要么需要自己编写CUDA程序（部署时需要大量优化）。

本文的DSVT无需自定义CUDA操作，能高效地作为3D感知网络的主干。DSVT包含 能在具有不同稀疏性的局部窗口并行计算的 动态稀疏窗口注意力，以及 进行下采样的、能更好地编码几何信息的、可学习的3D池化操作。

如上图所示，给点稀疏的体素表达，首先将每个窗口的稀疏体素划分为不重叠的子集，每个子集有相同的体素数，以便后续的并行计算。子集的分割方式会在相邻的自注意层中进行改变。这样，下一层可以进行前一层子集间的相互融合，以提高建模能力。同时，使用混合窗口分割，在相邻的Transformer块之间改变窗口大小，以进行多层次信息融合。实验表明，这样做可以提高性能并降低计算。通过批次处理的方式，所有区域的处理能完全并行。

对于3D稀疏池化操作，传统的基于3D稀疏卷积的方法需要的额外优化限制了部署，且为Transformer网络添加线性层或最大池化会影响性能。本文首先将稀疏下采样区域密集化，并以注意力方式进行3D池化，聚合局部空间特征。

3. 方法

3.1 概述

下图所示为本文的DSVT结构（柱体化表达）。首先通过体素特征编码（VFE）将点云进行体素化，其中每个体素称为一个token。由于Transformer感受野足够，且自动驾驶中物体的尺寸较小，本文使用单一步长网络而非层次结构网络。使用带有动态稀疏窗口注意力的DSVT块处理体素，且引入两种划分策略：旋转集合和混合窗口，分别进行窗口内和跨窗口特征传播。然后，使用可学习3D池化模块进行下采样，并压缩为BEV特征图输入任务头。

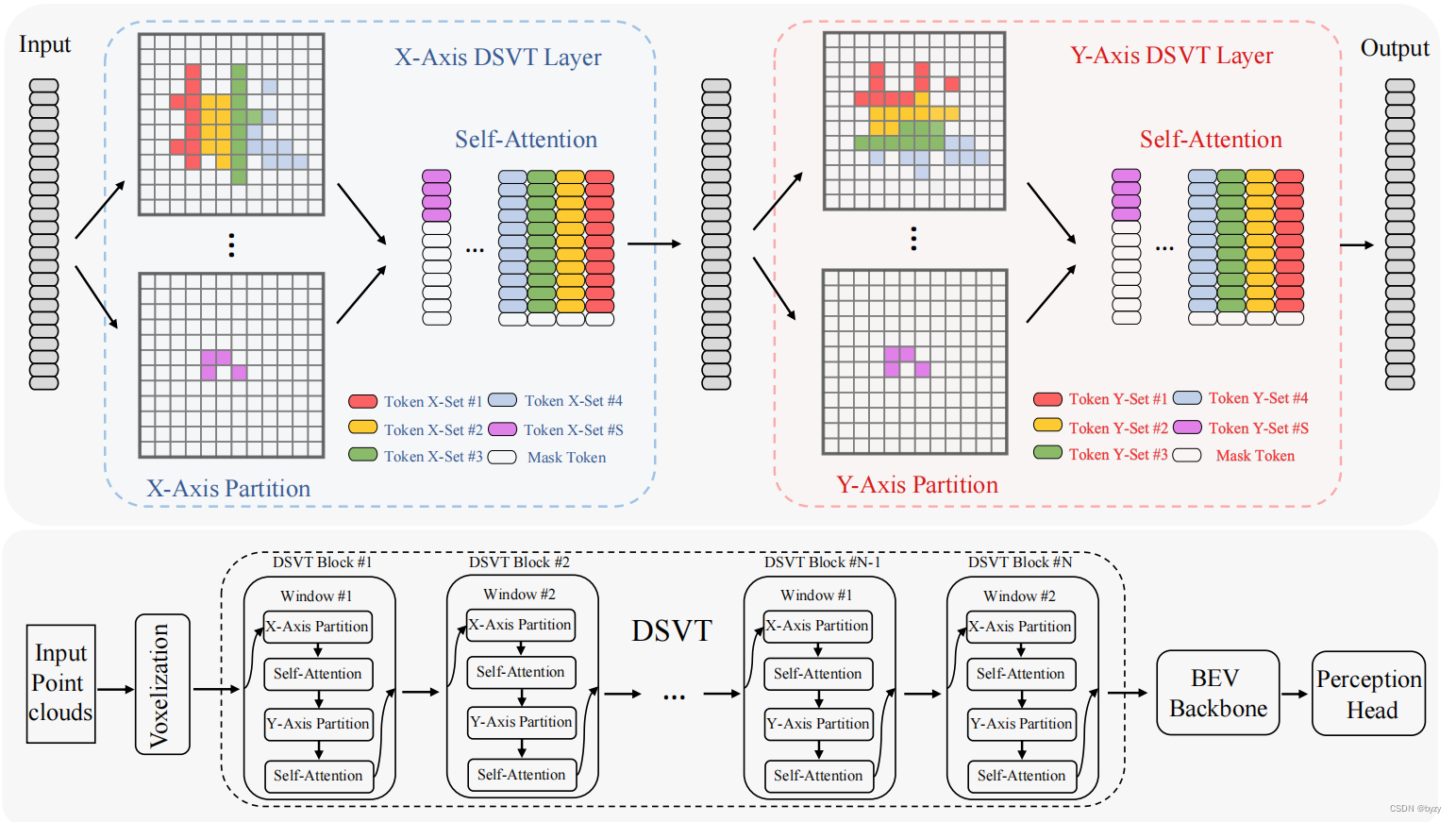
3.2 动态稀疏窗口注意力

本文提出动态稀疏窗口注意力，一种基于窗口的、高效并行处理3D体素的注意力策略，无需自定义CUDA操作。

动态集合划分：将token划分为窗口限制的、大小相同的子集。

首先将3D体素划分为固定大小的$L\times W\times H$的窗口。设某个窗口内含有$N$个非空体素：
V = { v i ∣ v i = [ ( x i , y i , z i ) ; f i ; d i ] } i = 1 N \mathcal{V}=\{v_i|v_i=[(x_i,y_i,z_i);f_i;d_i]\}_{i=1}^N V={vi?∣vi?=[(xi?,yi?,zi?);fi?;di?]}i=1N?
其中$(x_i,y_i,z_i)$为稀疏体素的坐标，$f_i\in {\mathbb{R}}^C$为体素特征。 d i ∈ { 1 , 2 , ? ? , N } d_i\in\{1,2,\cdots,N\} di?∈{1,2,?,N}为窗口内的体素ID，可通过某种体素排序策略得到。为生成不重叠的、大小相同的局部集合，首先计算需要的子集数量：
$$S=?\frac{N}{\tau }?+\mathbb{I}(N\%\tau >0)$$
其中$\mathbb{I}$为指示函数，$\tau$为集合内的最大非空体素数。$S$会根据窗口内体素的稀疏性动态变化。这样，非空体素越多的窗口会被分配更多的计算资源。

然后，将$N$个非空体素均匀分配给$S$个子集，第$j$个集合的第$k$个体素索引为
$$q_k^j=?\frac{j\times \tau +k}{S\times \tau }\times N?,k=0,1,?,\tau ?1$$
虽然上式会使得某些体素在子集中被复制多次，但这些冗余体素会被掩蔽（masked）。

得到第$j$个集合的划分结果 Q j = { q k j } k = 0 τ ? 1 \mathcal{Q}_j=\{q_k^j\}_{k=0}^{\tau-1} Qj?={qkj?}k=0τ?1?后，基于窗口内体素ID D = { d i } i = 1 N \mathcal{D}=\{d_i\}_{i=1}^N D={di?}i=1N?收集相应的体素特征${\mathcal{F}}_j\in {\mathbb{R}}^{\tau \times C}$和坐标${\mathcal{O}}_j\in {\mathbb{R}}^{\tau \times 3}$，记为：
$${\mathcal{F}}_j,{\mathcal{O}}_j=\text{INDEX}(\mathcal{V},{\mathcal{Q}}_j,\mathcal{D})$$

这样就能得到不重叠的、受窗口限制的、体素数量相同的集合。由于划分是基于窗口内体素ID得到的，可以通过重新排列体素来改变划分方式。

旋转集合注意力进行窗口内特征传播：上述方式能并行进行自注意力，但缺少集合间的交互。本文提出旋转集合注意力，在相邻的注意力层之间改变集合划分方式。

如前图所示，本文的DSVT块包含两种自注意力层，X轴划分（体素ID按照X坐标排列）和Y轴划分（体素ID按照Y坐标排列）。DSVT可按下式计算：
F l , O l = INDEX ( V l ? 1 , { Q j } j = 0 S ? 1 , D x ) V l = MHSA ( F l , PE ( O l ) ) F l + 1 , O l + 1 = INDEX ( V l , { Q j } j = 0 S ? 1 , D y ) V l + 1 = MHSA ( F l + 1 , PE ( O l + 1 ) ) \mathcal{F}^l,\mathcal{O}^l=\text{INDEX}(\mathcal{V}^{l-1},\{\mathcal{Q}_j\}_{j=0}^{S-1},\mathcal{D}_x)\\ \mathcal{V}^l=\text{MHSA}(\mathcal{F}^l,\text{PE}(\mathcal{O}^l))\\ \mathcal{F}^{l+1},\mathcal{O}^{l+1}=\text{INDEX}(\mathcal{V}^{l},\{\mathcal{Q}_j\}_{j=0}^{S-1},\mathcal{D}_y)\\ \mathcal{V}^{l+1}=\text{MHSA}(\mathcal{F}^{l+1},\text{PE}(\mathcal{O}^{l+1})) Fl,Ol=INDEX(Vl?1,{Qj?}j=0S?1?,Dx?)Vl=MHSA(Fl,PE(Ol))Fl+1,Ol+1=INDEX(Vl,{Qj?}j=0S?1?,Dy?)Vl+1=MHSA(Fl+1,PE(Ol+1))
其中${\mathcal{D}}_x,{\mathcal{D}}_y$分别为按X坐标和Y坐标排序后的体素索引。MHSA为带有FFN与层归一化的多头自注意力，PE为位置编码。

混合窗口分割进行跨窗口特征传播：为实现跨窗口体素交互，本文提出混合窗口划分。仅增加窗口的大小会减少计算，但也会导致小物体检测的性能下降。

本文在DSVT块之间使用与Swin-Transformer（见此文第二部分）类似的窗口移动技术，重新分割窗口，但窗口的大小会有所不同。

3.3 注意力形式的3D池化

填充稀疏区域并使用MLP进行下采样会降低性能，因为单层MLP无法从大量0填充结果中获取几何信息；此外也会损害网络优化。

本文提出注意力形式的3D池化操作。给定池化局部区域$l\times w\times h$，含$P$个非空体素 { p i } i = 1 P \{p_i\}_{i=1}^P {pi?}i=1P?，首先通过填充转化为密集区域 { p ~ i } i = 1 l × w × h \{\tilde{p}_i\}_{i=1}^{l\times w\times h} {p~?i?}i=1l×w×h?，然后沿体素维度使用最大池化：
P = MaxPool ( { p ~ i } i = 1 l × w × h ) \mathcal{P}=\text{MaxPool}(\{\tilde{p}_i\}_{i=1}^{l\times w\times h}) P=MaxPool({p~?i?}i=1l×w×h?)
将池化特征$\mathcal{P}$作为查询特征，未池化特征 { p ~ i } i = 1 l × w × h \{\tilde{p}_i\}_{i=1}^{l\times w\times h} {p~?i?}i=1l×w×h?作为键与值，进行注意力计算：
P ~ = Attn ( Q = P , K V = { p ~ i } i = 1 l × w × h ) \tilde{\mathcal{P}}=\text{Attn}(Q=\mathcal{P},KV=\{\tilde{p}_i\}_{i=1}^{l\times w\times h}) P~=Attn(Q=P,KV={p~?i?}i=1l×w×h?)
将上述结果输入到后续模块。

3.4 感知模型

主干网络变体：基于柱体表达的DSVT（DSVT-P），基于体素表达的DSVT（DSVT-V，仅在Z维度上使用3D池化逐步减小Z轴维度）。两个变体最终输出的体素数量和坐标均相同。

4. 实验

4.2 3D目标检测

本文的一阶段模型DSVT-V能超过之前最好的一阶段与二阶段模型，且与DSVT-P相比能大幅提升小物体的检测性能，证明了本文3D池化的捕捉细节几何信息的有效性。使用多帧输入（直接组合点云）时，本文的方法也能超过之前的多帧融合单阶段模型。

本文的两阶段模型也能在不同帧数的输入情况下超过过去的两阶段模型。

4.4 消融研究

与稀疏卷积主干相比：本文的DSVT有更高的性能和略高的延迟，但本文的方法能通过TensorRT进一步加速。

动态稀疏窗口划分的作用：与窗口密集化 + 自注意力的方案相比，本文的方法有更高的性能和更低的延迟。

为证明旋转集合划分的作用，本文的方法与随机集合划分（保证各集合内的体素在窗口内均匀分布）和一致集合划分（相邻注意力层之间不进行集合旋转）。实验表明一致集合划分优于随机集合划分，而旋转集合划分优于一致集合划分，因为其引入了集合间的交互。

3D池化模块的作用：与通过线性层池化、最大池化等方法相比，本文的方法能有更高的性能。为空体素添加掩膜（mask）会导致性能下降，这表明空体素也能编码物体几何信息。

4.5 推断速度

本文的方法经过TensorRT加速后能具有实时性（27Hz）。

补充材料

C. 超参数分析

集合大小：增大集合大小能提高性能，但过大的集合大小反而会略微降低性能。这是因为本文的局部区域集合自注意力可以更好地编码小物体的几何信息，而增大集合大小会引入噪声点。

网络深度：增大网络深度，性能会逐渐达到饱和，但延迟也会增加。