[足式机器人]Part2 Dr. CAN学习笔记-Ch00 - 数学知识基础
本文仅供学习使用
本文参考:
B站:DR_CAN
Dr. CAN学习笔记-Ch00 - 数学知识基础
1. Ch0-1矩阵的导数运算
1.1标量向量方程对向量求导,分母布局,分子布局
1.1.1 标量方程对向量的导数
-
y
y
y 为 一元向量 或 二元向量

-
y
y
y为多元向量
y ? = [ y 1 , y 2 , ? ? , y n ] ? ? f ( y ? ) ? y ? \vec{y}=\left[ y_1,y_2,\cdots ,y_{\mathrm{n}} \right] \Rightarrow \frac{\partial f\left( \vec{y} \right)}{\partial \vec{y}} y?=[y1?,y2?,?,yn?]??y??f(y?)?
其中: f ( y ? ) f\left( \vec{y} \right) f(y?) 为标量 1 × 1 1\times 1 1×1, y ? \vec{y} y?为向量 1 × n 1\times n 1×n
分母布局 Denominator Layout——行数与分母相同
? f ( y ? ) ? y ? = [ ? f ( y ? ) ? y 1 ? ? f ( y ? ) ? y n ] n × 1 \frac{\partial f\left( \vec{y} \right)}{\partial \vec{y}}=\left[ \begin{array}{c} \frac{\partial f\left( \vec{y} \right)}{\partial y_1}\\ \vdots\\ \frac{\partial f\left( \vec{y} \right)}{\partial y_{\mathrm{n}}}\\ \end{array} \right] _{n\times 1} ?y??f(y?)?= ??y1??f(y?)???yn??f(y?)?? ?n×1?分子布局 Nunerator Layout——行数与分子相同
? f ( y ? ) ? y ? = [ ? f ( y ? ) ? y 1 ? ? f ( y ? ) ? y n ] 1 × n \frac{\partial f\left( \vec{y} \right)}{\partial \vec{y}}=\left[ \begin{matrix} \frac{\partial f\left( \vec{y} \right)}{\partial y_1}& \cdots& \frac{\partial f\left( \vec{y} \right)}{\partial y_{\mathrm{n}}}\\ \end{matrix} \right] _{1\times n} ?y??f(y?)?=[?y1??f(y?)?????yn??f(y?)??]1×n?
1.1.2 向量方程对向量的导数
f
?
(
y
?
)
=
[
f
?
1
(
y
?
)
?
f
?
n
(
y
?
)
]
n
×
1
,
y
?
=
[
y
1
?
y
m
]
m
×
1
\vec{f}\left( \vec{y} \right) =\left[ \begin{array}{c} \vec{f}_1\left( \vec{y} \right)\\ \vdots\\ \vec{f}_{\mathrm{n}}\left( \vec{y} \right)\\ \end{array} \right] _{n\times 1},\vec{y}=\left[ \begin{array}{c} y_1\\ \vdots\\ y_{\mathrm{m}}\\ \end{array} \right] _{\mathrm{m}\times 1}
f?(y?)=
?f?1?(y?)?f?n?(y?)?
?n×1?,y?=
?y1??ym??
?m×1?
?
f
?
(
y
?
)
n
×
1
?
y
?
m
×
1
=
[
?
f
?
(
y
?
)
?
y
1
?
?
f
?
(
y
?
)
?
y
m
]
m
×
1
=
[
?
f
1
(
y
?
)
?
y
1
?
?
f
n
(
y
?
)
?
y
1
?
?
?
?
f
1
(
y
?
)
?
y
m
?
?
f
n
(
y
?
)
?
y
m
]
m
×
n
\frac{\partial \vec{f}\left( \vec{y} \right) _{n\times 1}}{\partial \vec{y}_{\mathrm{m}\times 1}}=\left[ \begin{array}{c} \frac{\partial \vec{f}\left( \vec{y} \right)}{\partial y_1}\\ \vdots\\ \frac{\partial \vec{f}\left( \vec{y} \right)}{\partial y_{\mathrm{m}}}\\ \end{array} \right] _{\mathrm{m}\times 1}=\left[ \begin{matrix} \frac{\partial f_1\left( \vec{y} \right)}{\partial y_1}& \cdots& \frac{\partial f_{\mathrm{n}}\left( \vec{y} \right)}{\partial y_1}\\ \vdots& \ddots& \vdots\\ \frac{\partial f_1\left( \vec{y} \right)}{\partial y_{\mathrm{m}}}& \cdots& \frac{\partial f_{\mathrm{n}}\left( \vec{y} \right)}{\partial y_{\mathrm{m}}}\\ \end{matrix} \right] _{\mathrm{m}\times \mathrm{n}}
?y?m×1??f?(y?)n×1??=
??y1??f?(y?)???ym??f?(y?)??
?m×1?=
??y1??f1?(y?)???ym??f1?(y?)???????y1??fn?(y?)???ym??fn?(y?)??
?m×n?, 为分母布局
若: y ? = [ y 1 ? y m ] m × 1 , A = [ a 11 ? a 1 n ? ? ? a m 1 ? a m n ] \vec{y}=\left[ \begin{array}{c} y_1\\ \vdots\\ y_{\mathrm{m}}\\ \end{array} \right] _{\mathrm{m}\times 1}, A=\left[ \begin{matrix} a_{11}& \cdots& a_{1\mathrm{n}}\\ \vdots& \ddots& \vdots\\ a_{\mathrm{m}1}& \cdots& a_{\mathrm{mn}}\\ \end{matrix} \right] y?= ?y1??ym?? ?m×1?,A= ?a11??am1??????a1n??amn?? ?, 则有:
- ? A y ? ? y ? = A T \frac{\partial A\vec{y}}{\partial \vec{y}}=A^{\mathrm{T}} ?y??Ay??=AT(分母布局)
- ? y ? T A y ? ? y ? = A y ? + A T y ? \frac{\partial \vec{y}^{\mathrm{T}}A\vec{y}}{\partial \vec{y}}=A\vec{y}+A^{\mathrm{T}}\vec{y} ?y??y?TAy??=Ay?+ATy?, 当 A = A T A=A^{\mathrm{T}} A=AT时, ? y ? T A y ? ? y ? = 2 A y ? \frac{\partial \vec{y}^{\mathrm{T}}A\vec{y}}{\partial \vec{y}}=2A\vec{y} ?y??y?TAy??=2Ay?
若为分子布局,则有: ? A y ? ? y ? = A \frac{\partial A\vec{y}}{\partial \vec{y}}=A ?y??Ay??=A
1.2 案例分析,线性回归
- ? A y ? ? y ? = A T \frac{\partial A\vec{y}}{\partial \vec{y}}=A^{\mathrm{T}} ?y??Ay??=AT(分母布局)
- ? y ? T A y ? ? y ? = A y ? + A T y ? \frac{\partial \vec{y}^{\mathrm{T}}A\vec{y}}{\partial \vec{y}}=A\vec{y}+A^{\mathrm{T}}\vec{y} ?y??y?TAy??=Ay?+ATy?, 当 A = A T A=A^{\mathrm{T}} A=AT时, ? y ? T A y ? ? y ? = 2 A y ? \frac{\partial \vec{y}^{\mathrm{T}}A\vec{y}}{\partial \vec{y}}=2A\vec{y} ?y??y?TAy??=2Ay?
Linear Regression 线性回归
z
^
=
y
1
+
y
2
x
?
J
=
∑
i
=
1
n
[
z
i
?
(
y
1
+
y
2
x
i
)
]
2
\hat{z}=y_1+y_2x\Rightarrow J=\sum_{i=1}^n{\left[ z_i-\left( y_1+y_2x_i \right) \right] ^2}
z^=y1?+y2?x?J=i=1∑n?[zi??(y1?+y2?xi?)]2
找到
y
1
,
y
2
y_1,y_2
y1?,y2? 使得
J
J
J最小
z
?
=
[
z
1
?
z
n
]
,
[
x
?
]
=
[
1
x
1
?
?
1
x
n
]
,
y
?
=
[
y
1
y
2
]
?
z
?
^
=
[
x
?
]
y
?
=
[
y
1
+
y
2
x
1
?
y
1
+
y
2
x
n
]
\vec{z}=\left[ \begin{array}{c} z_1\\ \vdots\\ z_{\mathrm{n}}\\ \end{array} \right] ,\left[ \vec{x} \right] =\left[ \begin{array}{l} 1& x_1\\ \vdots& \vdots\\ 1& x_{\mathrm{n}}\\ \end{array} \right] ,\vec{y}=\left[ \begin{array}{c} y_1\\ y_2\\ \end{array} \right] \Rightarrow \hat{\vec{z}}=\left[ \vec{x} \right] \vec{y}=\left[ \begin{array}{c} y_1+y_2x_1\\ \vdots\\ y_1+y_2x_{\mathrm{n}}\\ \end{array} \right]
z=
?z1??zn??
?,[x]=
?1?1?x1??xn??
?,y?=[y1?y2??]?z^=[x]y?=
?y1?+y2?x1??y1?+y2?xn??
?
J
=
[
z
?
?
z
?
^
]
T
[
z
?
?
z
?
^
]
=
[
z
?
?
[
x
?
]
y
?
]
T
[
z
?
?
[
x
?
]
y
?
]
=
z
?
z
?
T
?
z
?
T
[
x
?
]
y
?
?
y
?
T
[
x
?
]
T
z
?
+
y
?
T
[
x
?
]
T
[
x
?
]
y
?
J=\left[ \vec{z}-\hat{\vec{z}} \right] ^{\mathrm{T}}\left[ \vec{z}-\hat{\vec{z}} \right] =\left[ \vec{z}-\left[ \vec{x} \right] \vec{y} \right] ^{\mathrm{T}}\left[ \vec{z}-\left[ \vec{x} \right] \vec{y} \right] =\vec{z}\vec{z}^{\mathrm{T}}-\vec{z}^{\mathrm{T}}\left[ \vec{x} \right] \vec{y}-\vec{y}^{\mathrm{T}}\left[ \vec{x} \right] ^{\mathrm{T}}\vec{z}+\vec{y}^{\mathrm{T}}\left[ \vec{x} \right] ^{\mathrm{T}}\left[ \vec{x} \right] \vec{y}
J=[z?z^]T[z?z^]=[z?[x]y?]T[z?[x]y?]=zzT?zT[x]y??y?T[x]Tz+y?T[x]T[x]y?
其中:
(
z
?
T
[
x
?
]
y
?
)
T
=
y
?
T
[
x
?
]
T
z
?
\left( \vec{z}^{\mathrm{T}}\left[ \vec{x} \right] \vec{y} \right) ^{\mathrm{T}}=\vec{y}^{\mathrm{T}}\left[ \vec{x} \right] ^{\mathrm{T}}\vec{z}
(zT[x]y?)T=y?T[x]Tz, 则有:
J
=
z
?
z
?
T
?
2
z
?
T
[
x
?
]
y
?
+
y
?
T
[
x
?
]
T
[
x
?
]
y
?
J=\vec{z}\vec{z}^{\mathrm{T}}-2\vec{z}^{\mathrm{T}}\left[ \vec{x} \right] \vec{y}+\vec{y}^{\mathrm{T}}\left[ \vec{x} \right] ^{\mathrm{T}}\left[ \vec{x} \right] \vec{y}
J=zzT?2zT[x]y?+y?T[x]T[x]y?
进而:
?
J
?
y
?
=
0
?
2
(
z
?
T
[
x
?
]
)
T
+
2
[
x
?
]
T
[
x
?
]
y
?
=
?
y
?
?
?
J
?
y
?
?
=
0
,
y
?
?
=
(
[
x
?
]
T
[
x
?
]
)
?
1
[
x
?
]
T
z
?
\frac{\partial J}{\partial \vec{y}}=0-2\left( \vec{z}^{\mathrm{T}}\left[ \vec{x} \right] \right) ^{\mathrm{T}}+2\left[ \vec{x} \right] ^{\mathrm{T}}\left[ \vec{x} \right] \vec{y}=\nabla \vec{y}\Longrightarrow \frac{\partial J}{\partial \vec{y}^*}=0,\vec{y}^*=\left( \left[ \vec{x} \right] ^{\mathrm{T}}\left[ \vec{x} \right] \right) ^{-1}\left[ \vec{x} \right] ^{\mathrm{T}}\vec{z}
?y??J?=0?2(zT[x])T+2[x]T[x]y?=?y???y???J?=0,y??=([x]T[x])?1[x]Tz
其中:
(
[
x
?
]
T
[
x
?
]
)
?
1
\left( \left[ \vec{x} \right] ^{\mathrm{T}}\left[ \vec{x} \right] \right) ^{-1}
([x]T[x])?1不一定有解,则
y
?
?
\vec{y}^*
y??无法得到解析解——定义初始
y
?
?
\vec{y}^*
y??,
y
?
?
=
y
?
?
?
α
?
,
α
=
[
α
1
0
0
α
2
]
\vec{y}^*=\vec{y}^*-\alpha \nabla ,\alpha =\left[ \begin{matrix} \alpha _1& 0\\ 0& \alpha _2\\ \end{matrix} \right]
y??=y???α?,α=[α1?0?0α2??]
其中:
α
\alpha
α称为学习率,对
x
x
x而言则需进行归一化
1.3 矩阵求导的链式法则
标量函数: J = f ( y ( u ) ) , ? J ? u = ? J ? y ? y ? u J=f\left( y\left( u \right) \right) ,\frac{\partial J}{\partial u}=\frac{\partial J}{\partial y}\frac{\partial y}{\partial u} J=f(y(u)),?u?J?=?y?J??u?y?
标量对向量求导: J = f ( y ? ( u ? ) ) , y ? = [ y 1 ( u ? ) ? y m ( u ? ) ] m × 1 , u ? = [ u ? 1 ? u ? n ] n × 1 J=f\left( \vec{y}\left( \vec{u} \right) \right) ,\vec{y}=\left[ \begin{array}{c} y_1\left( \vec{u} \right)\\ \vdots\\ y_{\mathrm{m}}\left( \vec{u} \right)\\ \end{array} \right] _{m\times 1},\vec{u}=\left[ \begin{array}{c} \vec{u}_1\\ \vdots\\ \vec{u}_{\mathrm{n}}\\ \end{array} \right] _{\mathrm{n}\times 1} J=f(y?(u)),y?= ?y1?(u)?ym?(u)? ?m×1?,u= ?u1??un?? ?n×1?
分析: ? J 1 × 1 ? u n × 1 n × 1 = ? J ? y m × 1 m × 1 ? y m × 1 ? u n × 1 n × m \frac{\partial J_{1\times 1}}{\partial u_{\mathrm{n}\times 1}}_{\mathrm{n}\times 1}=\frac{\partial J}{\partial y_{m\times 1}}_{m\times 1}\frac{\partial y_{m\times 1}}{\partial u_{\mathrm{n}\times 1}}_{\mathrm{n}\times \mathrm{m}} ?un×1??J1×1??n×1?=?ym×1??J?m×1??un×1??ym×1??n×m? 无法相乘
y ? = [ y 1 ( u ? ) y 2 ( u ? ) ] 2 × 1 , u ? = [ u ? 1 u ? 2 u ? 3 ] 3 × 1 \vec{y}=\left[ \begin{array}{c} y_1\left( \vec{u} \right)\\ y_2\left( \vec{u} \right)\\ \end{array} \right] _{2\times 1},\vec{u}=\left[ \begin{array}{c} \vec{u}_1\\ \vec{u}_2\\ \vec{u}_3\\ \end{array} \right] _{3\times 1} y?=[y1?(u)y2?(u)?]2×1?,u= ?u1?u2?u3?? ?3×1?
J = f ( y ? ( u ? ) ) , ? J ? u ? = [ ? J ? u ? 1 ? J ? u ? 2 ? J ? u ? 3 ] 3 × 1 ? ? J ? u ? 1 = ? J ? y 1 ? y 1 ( u ? ) ? u ? 1 + ? J ? y 2 ? y 2 ( u ? ) ? u ? 1 ? J ? u ? 2 = ? J ? y 1 ? y 1 ( u ? ) ? u ? 2 + ? J ? y 2 ? y 2 ( u ? ) ? u ? 2 ? J ? u ? 3 = ? J ? y 1 ? y 1 ( u ? ) ? u ? 3 + ? J ? y 2 ? y 2 ( u ? ) ? u ? 3 ? ? J ? u ? = [ ? y 1 ( u ? ) ? u ? 1 ? y 2 ( u ? ) ? u ? 1 ? y 1 ( u ? ) ? u ? 2 ? y 2 ( u ? ) ? u ? 2 ? y 1 ( u ? ) ? u ? 3 ? y 2 ( u ? ) ? u ? 3 ] 3 × 2 [ ? J ? y 1 ? J ? y 2 ] 2 × 2 = ? y ? ( u ? ) ? u ? ? J ? y ? J=f\left( \vec{y}\left( \vec{u} \right) \right) ,\frac{\partial J}{\partial \vec{u}}=\left[ \begin{array}{c} \frac{\partial J}{\partial \vec{u}_1}\\ \frac{\partial J}{\partial \vec{u}_2}\\ \frac{\partial J}{\partial \vec{u}_3}\\ \end{array} \right] _{3\times 1}\Longrightarrow \begin{array}{c} \frac{\partial J}{\partial \vec{u}_1}=\frac{\partial J}{\partial y_1}\frac{\partial y_1\left( \vec{u} \right)}{\partial \vec{u}_1}+\frac{\partial J}{\partial y_2}\frac{\partial y_2\left( \vec{u} \right)}{\partial \vec{u}_1}\\ \frac{\partial J}{\partial \vec{u}_2}=\frac{\partial J}{\partial y_1}\frac{\partial y_1\left( \vec{u} \right)}{\partial \vec{u}_2}+\frac{\partial J}{\partial y_2}\frac{\partial y_2\left( \vec{u} \right)}{\partial \vec{u}_2}\\ \frac{\partial J}{\partial \vec{u}_3}=\frac{\partial J}{\partial y_1}\frac{\partial y_1\left( \vec{u} \right)}{\partial \vec{u}_3}+\frac{\partial J}{\partial y_2}\frac{\partial y_2\left( \vec{u} \right)}{\partial \vec{u}_3}\\ \end{array} \\ \Longrightarrow \frac{\partial J}{\partial \vec{u}}=\left[ \begin{array}{l} \frac{\partial y_1\left( \vec{u} \right)}{\partial \vec{u}_1}& \frac{\partial y_2\left( \vec{u} \right)}{\partial \vec{u}_1}\\ \frac{\partial y_1\left( \vec{u} \right)}{\partial \vec{u}_2}& \frac{\partial y_2\left( \vec{u} \right)}{\partial \vec{u}_2}\\ \frac{\partial y_1\left( \vec{u} \right)}{\partial \vec{u}_3}& \frac{\partial y_2\left( \vec{u} \right)}{\partial \vec{u}_3}\\ \end{array} \right] _{3\times 2}\left[ \begin{array}{c} \frac{\partial J}{\partial y_1}\\ \frac{\partial J}{\partial y_2}\\ \end{array} \right] _{2\times 2}=\frac{\partial \vec{y}\left( \vec{u} \right)}{\partial \vec{u}}\frac{\partial J}{\partial \vec{y}} J=f(y?(u)),?u?J?= ??u1??J??u2??J??u3??J?? ?3×1???u1??J?=?y1??J??u1??y1?(u)?+?y2??J??u1??y2?(u)??u2??J?=?y1??J??u2??y1?(u)?+?y2??J??u2??y2?(u)??u3??J?=?y1??J??u3??y1?(u)?+?y2??J??u3??y2?(u)????u?J?= ??u1??y1?(u)??u2??y1?(u)??u3??y1?(u)???u1??y2?(u)??u2??y2?(u)??u3??y2?(u)?? ?3×2?[?y1??J??y2??J??]2×2?=?u?y?(u)??y??J?
? J ? u ? = ? y ? ( u ? ) ? u ? ? J ? y ? \frac{\partial J}{\partial \vec{u}}=\frac{\partial \vec{y}\left( \vec{u} \right)}{\partial \vec{u}}\frac{\partial J}{\partial \vec{y}} ?u?J?=?u?y?(u)??y??J?
eg:
x
?
[
k
+
1
]
=
A
x
?
[
k
]
+
B
u
?
[
k
]
,
J
=
x
?
T
[
k
+
1
]
x
?
[
k
+
1
]
\vec{x}\left[ k+1 \right] =A\vec{x}\left[ k \right] +B\vec{u}\left[ k \right] ,J=\vec{x}^{\mathrm{T}}\left[ k+1 \right] \vec{x}\left[ k+1 \right]
x[k+1]=Ax[k]+Bu[k],J=xT[k+1]x[k+1]
?
J
?
u
?
=
?
x
?
[
k
+
1
]
?
u
?
?
J
?
x
?
[
k
+
1
]
=
B
T
?
2
x
?
[
k
+
1
]
=
2
B
T
x
?
[
k
+
1
]
\frac{\partial J}{\partial \vec{u}}=\frac{\partial \vec{x}\left[ k+1 \right]}{\partial \vec{u}}\frac{\partial J}{\partial \vec{x}\left[ k+1 \right]}=B^{\mathrm{T}}\cdot 2\vec{x}\left[ k+1 \right] =2B^{\mathrm{T}}\vec{x}\left[ k+1 \right]
?u?J?=?u?x[k+1]??x[k+1]?J?=BT?2x[k+1]=2BTx[k+1]
2. Ch0-2 特征值与特征向量
2.1 定义
A
v
?
=
λ
v
?
A\vec{v}=\lambda \vec{v}
Av=λv
对于给定线性变换
A
A
A,特征向量eigenvector
v
?
\vec{v}
v 在此变换后仍与原来的方向共线,但长度可能会发生改变,其中
λ
\lambda
λ 为标量,即缩放比例,称其为特征值eigenvalue
2.1.1 线性变换

2.1.2 求解特征值,特征向量
A
v
?
=
λ
v
?
?
(
A
?
λ
E
)
v
?
=
0
?
∣
A
?
λ
E
∣
=
0
A\vec{v}=\lambda \vec{v}\Rightarrow \left( A-\lambda E \right) \vec{v}=0\Rightarrow \left| A-\lambda E \right|=0
Av=λv?(A?λE)v=0?∣A?λE∣=0

2.1.3 应用:对角化矩阵——解耦Decouple
P = [ v ? 1 , v ? 2 ] P=\left[ \vec{v}_1,\vec{v}_2 \right] P=[v1?,v2?]—— coordinate transformation matrix
A P = A [ v ? 1 v ? 2 ] = [ A [ v 11 v 12 ] A [ v 21 v 22 ] ] = [ λ 1 v 11 λ 2 v 21 λ 1 v 12 λ 2 v 22 ] = [ v 11 v 21 v 12 v 22 ] [ λ 1 0 0 λ 2 ] = P Λ ? A P = P Λ ? P ? 1 A P = Λ AP=A\left[ \begin{matrix} \vec{v}_1& \vec{v}_2\\ \end{matrix} \right] =\left[ \begin{matrix} A\left[ \begin{array}{c} v_{11}\\ v_{12}\\ \end{array} \right]& A\left[ \begin{array}{c} v_{21}\\ v_{22}\\ \end{array} \right]\\ \end{matrix} \right] =\left[ \begin{matrix} \lambda _1v_{11}& \lambda _2v_{21}\\ \lambda _1v_{12}& \lambda _2v_{22}\\ \end{matrix} \right] =\left[ \begin{matrix} v_{11}& v_{21}\\ v_{12}& v_{22}\\ \end{matrix} \right] \left[ \begin{matrix} \lambda _1& 0\\ 0& \lambda _2\\ \end{matrix} \right] =P\varLambda \\ \Rightarrow AP=P\varLambda \Rightarrow P^{-1}AP=\varLambda AP=A[v1??v2??]=[A[v11?v12??]?A[v21?v22??]?]=[λ1?v11?λ1?v12??λ2?v21?λ2?v22??]=[v11?v12??v21?v22??][λ1?0?0λ2??]=PΛ?AP=PΛ?P?1AP=Λ
- 微分方程组 state-space rep
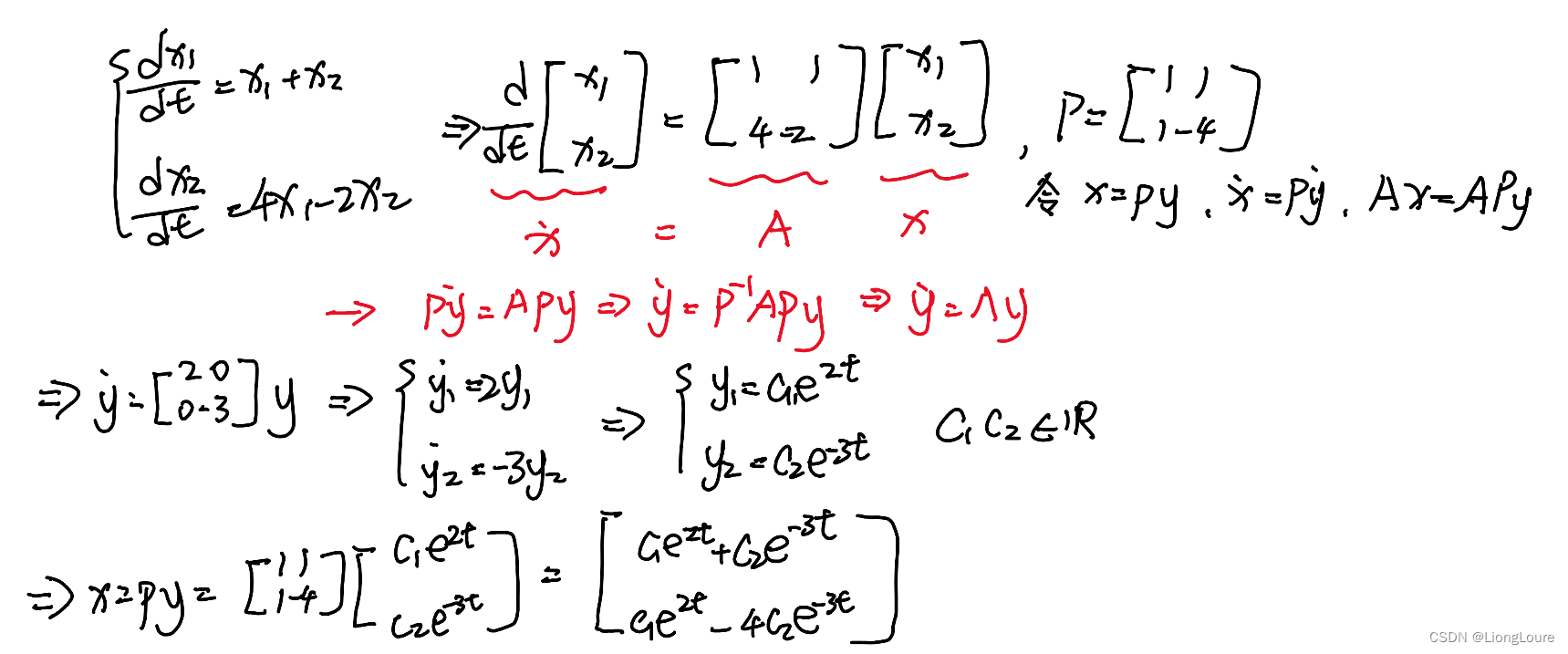
2.2 Summary
- A v ? = λ v ? A\vec{v}=\lambda \vec{v} Av=λv 在一条直线上
- 求解方法: ∣ A ? λ E ∣ = 0 \left| A-\lambda E \right|=0 ∣A?λE∣=0
- P ? 1 A P = Λ , P = [ v ? 1 v ? 2 ? ] , Λ = [ λ 1 λ 2 ? ] P^{-1}AP=\varLambda , P=\left[ \begin{matrix} \vec{v}_1& \vec{v}_2& \cdots\\ \end{matrix} \right] , \varLambda =\left[ \begin{matrix} \lambda _1& & \\ & \lambda _2& \\ & & \ddots\\ \end{matrix} \right] P?1AP=Λ,P=[v1??v2????],Λ= ?λ1??λ2???? ?
- x ˙ = A x , x = P y , y ˙ = Λ y \dot{x}=Ax, x=Py,\dot{y}=\varLambda y x˙=Ax,x=Py,y˙?=Λy
3. Ch0-3线性化Linearization
3.1 线性系统 Linear System 与 叠加原理 Superposition
x ˙ = f ( x ) \dot{x}=f\left( x \right) x˙=f(x)
- x 1 , x 2 x_1,x_2 x1?,x2? 是解
- x 3 = k 1 x 1 + k 2 x 2 , k 1 , k 2 ∈ R x_3=k_1x_1+k_2x_2,k_1,k_2\in \mathbb{R} x3?=k1?x1?+k2?x2?,k1?,k2?∈R
- x 3 x_3 x3? 是解
eg:
x
¨
+
2
x
˙
+
2
x
=
0
√
x
¨
+
2
x
˙
+
2
x
2
=
0
×
x
¨
+
sin
?
x
˙
+
2
x
=
0
×
\ddot{x}+2\dot{x}+\sqrt{2}x=0 √ \\ \ddot{x}+2\dot{x}+\sqrt{2}x^2=0 × \\ \ddot{x}+\sin \dot{x}+\sqrt{2}x=0 ×
x¨+2x˙+2?x=0√x¨+2x˙+2?x2=0×x¨+sinx˙+2?x=0×
3.2 线性化:Taylor Series
f ( x ) = f ( x 0 ) + f ′ ( x 0 ) 1 ! ( x ? x 0 ) + f ′ ′ ( x 0 ) 2 ! ( x ? x 0 ) 2 + ? + f n ( x 0 ) n ! ( x ? x 0 ) n f\left( x \right) =f\left( x_0 \right) +\frac{f^{\prime}\left( x_0 \right)}{1!}\left( x-x_0 \right) +\frac{{f^{\prime}}^{\prime}\left( x_0 \right)}{2!}\left( x-x_0 \right) ^2+\cdots +\frac{f^n\left( x_0 \right)}{n!}\left( x-x_0 \right) ^n f(x)=f(x0?)+1!f′(x0?)?(x?x0?)+2!f′′(x0?)?(x?x0?)2+?+n!fn(x0?)?(x?x0?)n
若 x ? x 0 → 0 , ( x ? x 0 ) n → 0 x-x_0\rightarrow 0,\left( x-x_0 \right) ^n\rightarrow 0 x?x0?→0,(x?x0?)n→0,则有: ? f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x ? x 0 ) ? f ( x ) = k 1 + k 2 x ? k 3 x 0 ? f ( x ) = k 2 x + b \Rightarrow f\left( x \right) =f\left( x_0 \right) +f^{\prime}\left( x_0 \right) \left( x-x_0 \right) \Rightarrow f\left( x \right) =k_1+k_2x-k_3x_0\Rightarrow f\left( x \right) =k_2x+b ?f(x)=f(x0?)+f′(x0?)(x?x0?)?f(x)=k1?+k2?x?k3?x0??f(x)=k2?x+b

eg1:

eg2:

eg3:
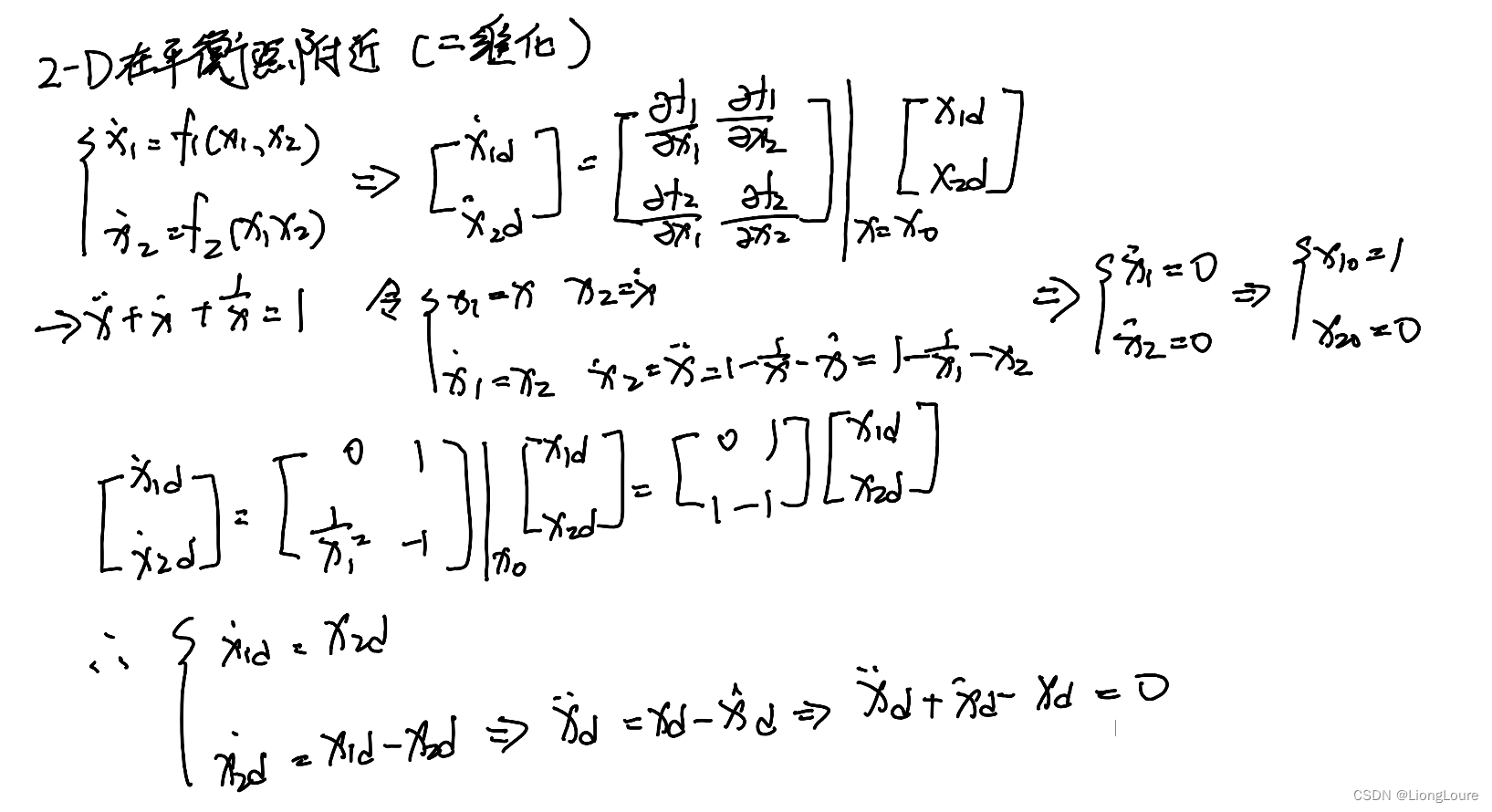
3.3 Summary
- f ( x ) = f ( x 0 ) + f ′ ( x 0 ) 1 ! ( x ? x 0 ) , x ? x 0 → 0 f\left( x \right) =f\left( x_0 \right) +\frac{f^{\prime}\left( x_0 \right)}{1!}\left( x-x_0 \right) ,x-x_0\rightarrow 0 f(x)=f(x0?)+1!f′(x0?)?(x?x0?),x?x0?→0
- [ x ˙ 1 d x ˙ 2 d ] = [ ? f 1 ? x 1 ? f 1 ? x 2 ? f 2 ? x 1 ? f 2 ? x 2 ] ∣ x = x 0 [ x 1 d x 2 d ] \left[ \begin{array}{c} \dot{x}_{1\mathrm{d}}\\ \dot{x}_{2\mathrm{d}}\\ \end{array} \right] =\left. \left[ \begin{matrix} \frac{\partial f_1}{\partial x_1}& \frac{\partial f_1}{\partial x_2}\\ \frac{\partial f_2}{\partial x_1}& \frac{\partial f_2}{\partial x_2}\\ \end{matrix} \right] \right|_{\mathrm{x}=\mathrm{x}_0}\left[ \begin{array}{c} x_{1\mathrm{d}}\\ x_{2\mathrm{d}}\\ \end{array} \right] [x˙1d?x˙2d??]=[?x1??f1???x1??f2????x2??f1???x2??f2???] ?x=x0??[x1d?x2d??]
4. Ch0-4线性时不变系统中的冲激响应与卷积
4.1 LIT System:Linear Time Invariant
-
运算operator : O { ? } O\left\{ \cdot \right\} O{?}
I n p u t O { f ( t ) } = o u t p u t x ( t ) \begin{array}{c} Input\\ O\left\{ f\left( t \right) \right\}\\ \end{array}=\begin{array}{c} output\\ x\left( t \right)\\ \end{array} InputO{f(t)}?=outputx(t)? -
线性——
叠加原理superpositin principle:
{ O { f 1 ( t ) + f 2 ( t ) } = x 1 ( t ) + x 2 ( t ) O { a f 1 ( t ) } = a x 1 ( t ) O { a 1 f 1 ( t ) + a 2 f 2 ( t ) } = a 1 x 1 ( t ) + a 2 x 2 ( t ) \begin{cases} O\left\{ f_1\left( t \right) +f_2\left( t \right) \right\} =x_1\left( t \right) +x_2\left( t \right)\\ O\left\{ af_1\left( t \right) \right\} =ax_1\left( t \right)\\ O\left\{ a_1f_1\left( t \right) +a_2f_2\left( t \right) \right\} =a_1x_1\left( t \right) +a_2x_2\left( t \right)\\ \end{cases} ? ? ??O{f1?(t)+f2?(t)}=x1?(t)+x2?(t)O{af1?(t)}=ax1?(t)O{a1?f1?(t)+a2?f2?(t)}=a1?x1?(t)+a2?x2?(t)? -
时不变Time Invariant:
O { f ( t ) } = x ( t ) ? O { f ( t ? τ ) } = x ( t ? τ ) O\left\{ f\left( t \right) \right\} =x\left( t \right) \Rightarrow O\left\{ f\left( t-\tau \right) \right\} =x\left( t-\tau \right) O{f(t)}=x(t)?O{f(t?τ)}=x(t?τ)
4.2 卷积 Convolution

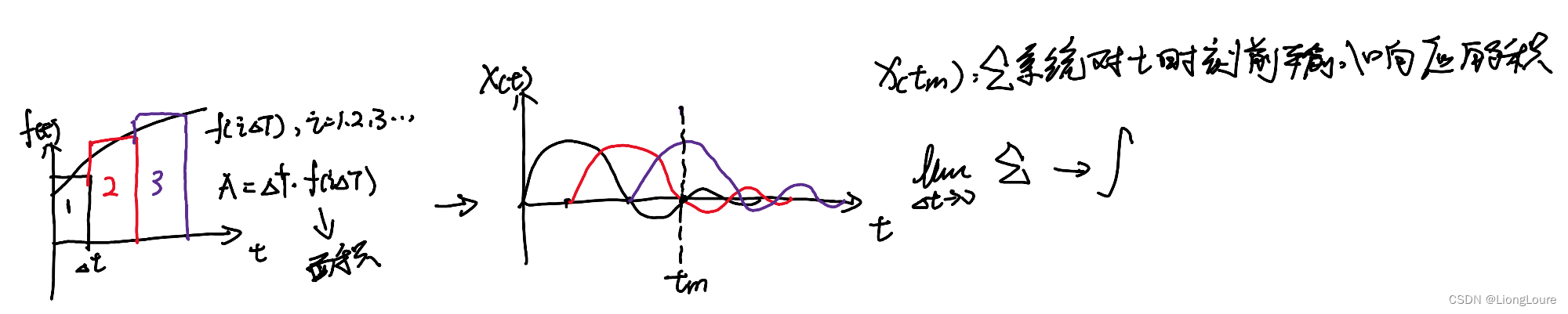
4.3 单位冲激 Unit Impulse——Dirac Delta
LIT系统,h(t)可以完全定义系统

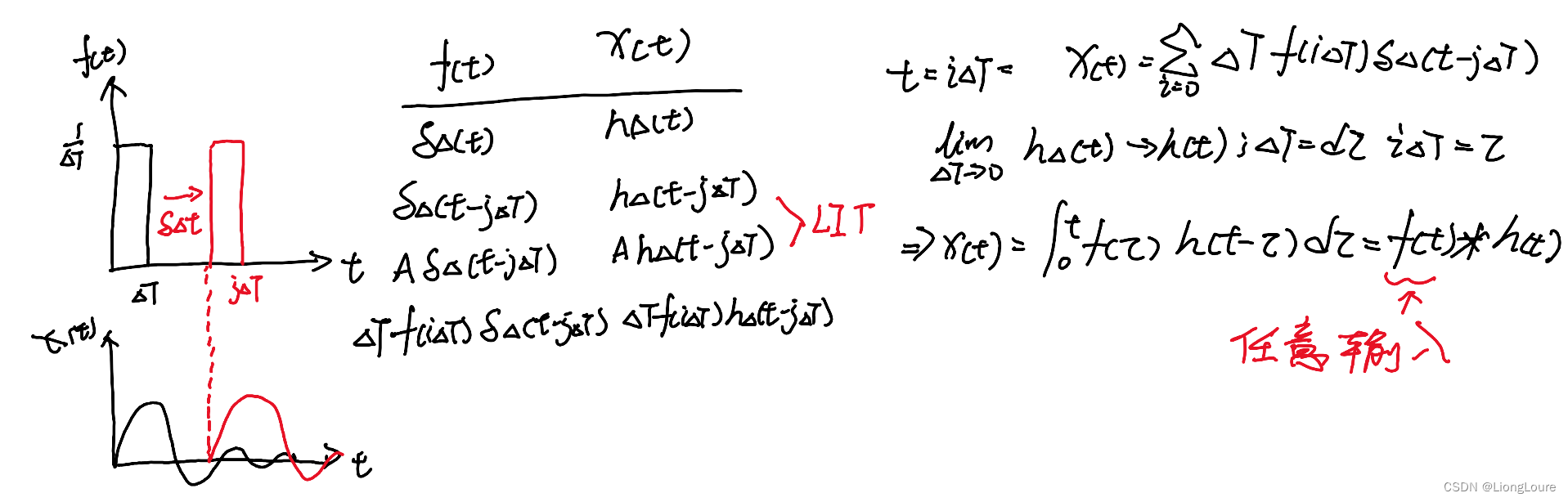
5. Ch0-5Laplace Transform of Convolution卷积的拉普拉斯变换
线性时不变系统 : LIT System
冲激响应:Impluse Response
卷积:Convolution
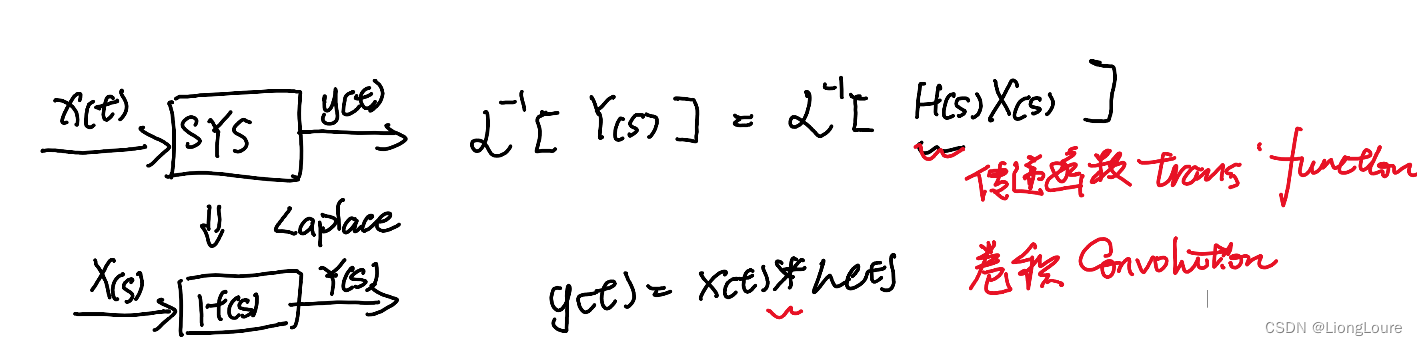
Laplace Transform : X ( s ) = L [ x ( t ) ] = ∫ 0 ∞ x ( t ) e ? s t d t X\left( s \right) =\mathcal{L} \left[ x\left( t \right) \right] =\int_0^{\infty}{x\left( t \right) e^{-st}}\mathrm{d}t X(s)=L[x(t)]=∫0∞?x(t)e?stdt
Convolution : x ( t ) ? g ( t ) = ∫ 0 t x ( τ ) g ( t ? τ ) d τ x\left( t \right) *g\left( t \right) =\int_0^t{x\left( \tau \right) g\left( t-\tau \right)}\mathrm{d}\tau x(t)?g(t)=∫0t?x(τ)g(t?τ)dτ
证明: L [ x ( t ) ? g ( t ) ] = X ( s ) G ( s ) \mathcal{L} \left[ x\left( t \right) *g\left( t \right) \right] =X\left( s \right) G\left( s \right) L[x(t)?g(t)]=X(s)G(s)
L [ x ( t ) ? g ( t ) ] = ∫ 0 ∞ ∫ 0 t x ( τ ) g ( t ? τ ) d τ e ? s t d t = ∫ 0 ∞ ∫ τ ∞ x ( τ ) g ( t ? τ ) e ? s t d t d τ \mathcal{L} \left[ x\left( t \right) *g\left( t \right) \right] =\int_0^{\infty}{\int_0^t{x\left( \tau \right) g\left( t-\tau \right) \mathrm{d}\tau}e^{-st}}\mathrm{d}t=\int_0^{\infty}{\int_{\tau}^{\infty}{x\left( \tau \right) g\left( t-\tau \right)}e^{-st}}\mathrm{d}t\mathrm{d}\tau L[x(t)?g(t)]=∫0∞?∫0t?x(τ)g(t?τ)dτe?stdt=∫0∞?∫τ∞?x(τ)g(t?τ)e?stdtdτ
>令: u = t ? τ , t = u + τ , d t = d u + d τ , t ∈ [ τ , + ∞ ) ? u ∈ [ 0 , + ∞ ) u=t-\tau ,t=u+\tau ,\mathrm{d}t=\mathrm{d}u+\mathrm{d}\tau ,t\in \left[ \tau ,+\infty \right) \Rightarrow u\in \left[ 0,+\infty \right) u=t?τ,t=u+τ,dt=du+dτ,t∈[τ,+∞)?u∈[0,+∞)
L [ x ( t ) ? g ( t ) ] = ∫ 0 ∞ ∫ 0 ∞ x ( τ ) g ( u ) e ? s ( u + τ ) d u d τ = ∫ 0 ∞ x ( τ ) e ? s τ d τ ∫ 0 ∞ g ( u ) e ? s u d u = X ( s ) G ( s ) \mathcal{L} \left[ x\left( t \right) *g\left( t \right) \right] =\int_0^{\infty}{\int_0^{\infty}{x\left( \tau \right) g\left( u \right)}e^{-s\left( u+\tau \right)}}\mathrm{d}u\mathrm{d}\tau =\int_0^{\infty}{x\left( \tau \right)}e^{-s\tau}\mathrm{d}\tau \int_0^{\infty}{g\left( u \right)}e^{-su}\mathrm{d}u=X\left( s \right) G\left( s \right) L[x(t)?g(t)]=∫0∞?∫0∞?x(τ)g(u)e?s(u+τ)dudτ=∫0∞?x(τ)e?sτdτ∫0∞?g(u)e?sudu=X(s)G(s)
L [ x ( t ) ? g ( t ) ] = L [ x ( t ) ] L [ g ( t ) ] = X ( s ) G ( s ) \mathcal{L} \left[ x\left( t \right) *g\left( t \right) \right] =\mathcal{L} \left[ x\left( t \right) \right] \mathcal{L} \left[ g\left( t \right) \right] =X\left( s \right) G\left( s \right) L[x(t)?g(t)]=L[x(t)]L[g(t)]=X(s)G(s)
6. Ch0-6复数Complex Number
x 2 ? 2 x + 2 = 0 ? x = 1 ± i x^2-2x+2=0\Rightarrow x=1\pm i x2?2x+2=0?x=1±i
- 代数表达:
z
=
a
+
b
i
,
R
e
(
z
)
=
a
,
I
m
(
z
)
=
b
z=a+bi,\mathrm{Re}\left( z \right) =a,\mathrm{Im}\left( z \right) =b
z=a+bi,Re(z)=a,Im(z)=b, 分别称为
实部与虚部 - 几何表达:
z
=
∣
z
∣
cos
?
θ
+
∣
z
∣
sin
?
θ
i
=
∣
z
∣
(
cos
?
θ
+
sin
?
θ
i
)
z=\left| z \right|\cos \theta +\left| z \right|\sin \theta i=\left| z \right|\left( \cos \theta +\sin \theta i \right)
z=∣z∣cosθ+∣z∣sinθi=∣z∣(cosθ+sinθi)

- 指数表达: z = ∣ z ∣ e i θ z=\left| z \right|e^{i\theta} z=∣z∣eiθ
z 1 = ∣ z 1 ∣ e i θ 1 , z 2 = ∣ z 2 ∣ e i θ 2 ? z 1 ? z 2 = ∣ z 1 ∣ ∣ z 2 ∣ e i ( θ 1 + θ 2 ) z_1=\left| z_1 \right|e^{i\theta _1},z_2=\left| z_2 \right|e^{i\theta _2}\Rightarrow z_1\cdot z_2=\left| z_1 \right|\left| z_2 \right|e^{i\left( \theta _1+\theta _2 \right)} z1?=∣z1?∣eiθ1?,z2?=∣z2?∣eiθ2??z1??z2?=∣z1?∣∣z2?∣ei(θ1?+θ2?)

共轭: z 1 = a 1 + b 1 i , z 2 = a 2 ? b 2 i ? z 1 = z ˉ 2 z_1=a_1+b_1i,z_2=a_2-b_2i\Rightarrow z_1=\bar{z}_2 z1?=a1?+b1?i,z2?=a2??b2?i?z1?=zˉ2?

7. Ch0-7欧拉公式的证明
更有意思的版本
e
i
θ
=
cos
?
θ
+
sin
?
θ
i
,
i
=
?
1
e^{i\theta}=\cos \theta +\sin \theta i,i=\sqrt{-1}
eiθ=cosθ+sinθi,i=?1?
证明:
f
(
θ
)
=
e
i
θ
cos
?
θ
+
sin
?
θ
i
f
′
(
θ
)
=
i
e
i
θ
(
cos
?
θ
+
sin
?
θ
i
)
?
e
i
θ
(
?
sin
?
θ
+
cos
?
θ
i
)
(
cos
?
θ
+
sin
?
θ
i
)
2
=
0
?
f
(
θ
)
=
c
o
n
s
tan
?
t
f
(
θ
)
=
f
(
0
)
=
e
i
0
cos
?
0
+
sin
?
0
i
=
1
?
e
i
θ
cos
?
θ
+
sin
?
θ
i
=
1
?
e
i
θ
=
cos
?
θ
+
sin
?
θ
i
f\left( \theta \right) =\frac{e^{i\theta}}{\cos \theta +\sin \theta i} \\ f^{\prime}\left( \theta \right) =\frac{ie^{i\theta}\left( \cos \theta +\sin \theta i \right) -e^{i\theta}\left( -\sin \theta +\cos \theta i \right)}{\left( \cos \theta +\sin \theta i \right) ^2}=0 \\ \Rightarrow f\left( \theta \right) =\mathrm{cons}\tan\mathrm{t} \\ f\left( \theta \right) =f\left( 0 \right) =\frac{e^{i0}}{\cos 0+\sin 0i}=1\Rightarrow \frac{e^{i\theta}}{\cos \theta +\sin \theta i}=1 \\ \Rightarrow e^{i\theta}=\cos \theta +\sin \theta i
f(θ)=cosθ+sinθieiθ?f′(θ)=(cosθ+sinθi)2ieiθ(cosθ+sinθi)?eiθ(?sinθ+cosθi)?=0?f(θ)=constantf(θ)=f(0)=cos0+sin0iei0?=1?cosθ+sinθieiθ?=1?eiθ=cosθ+sinθi
求解: sin ? x = 2 \sin x=2 sinx=2
令: sin ? z = 2 = c , z ∈ C \sin z=2=c,z\in \mathbb{C} sinz=2=c,z∈C
{ e i z = cos ? z + sin ? z i e i ( ? z ) = cos ? z ? sin ? z i ? e i z ? e ? i z = 2 sin ? z i \begin{cases} e^{iz}=\cos z+\sin zi\\ e^{i\left( -z \right)}=\cos z-\sin zi\\ \end{cases}\Rightarrow e^{iz}-e^{-iz}=2\sin zi {eiz=cosz+sinziei(?z)=cosz?sinzi??eiz?e?iz=2sinzi
∴ sin ? z = e i z ? e ? i z 2 i = c ? e a i ? b ? e b ? a i 2 i = e a i e ? b ? e b e ? a i 2 i = c \therefore \sin z=\frac{e^{iz}-e^{-iz}}{2i}=c\Rightarrow \frac{e^{ai-b}-e^{b-ai}}{2i}=\frac{e^{ai}e^{-b}-e^be^{-ai}}{2i}=c ∴sinz=2ieiz?e?iz?=c?2ieai?b?eb?ai?=2ieaie?b?ebe?ai?=c
且有: { e i a = cos ? a + sin ? a i e i ( ? a ) = cos ? a ? sin ? a i \begin{cases} e^{ia}=\cos a+\sin ai\\ e^{i\left( -a \right)}=\cos a-\sin ai\\ \end{cases} {eia=cosa+sinaiei(?a)=cosa?sinai?
? e ? b ( cos ? a + sin ? a i ) ? e b ( cos ? a ? sin ? a i ) 2 i = ( e ? b ? e b ) cos ? a ? ( e ? b + e b ) sin ? a i 2 i = c ? 1 2 ( e b ? e ? b ) cos ? a i + 1 2 ( e ? b + e b ) sin ? a = c = c + 0 i \Rightarrow \frac{e^{-b}\left( \cos a+\sin ai \right) -e^b\left( \cos a-\sin ai \right)}{2i}=\frac{\left( e^{-b}-e^b \right) \cos a-\left( e^{-b}+e^b \right) \sin ai}{2i}=c \\ \Rightarrow \frac{1}{2}\left( e^b-e^{-b} \right) \cos ai+\frac{1}{2}\left( e^{-b}+e^b \right) \sin a=c=c+0i ?2ie?b(cosa+sinai)?eb(cosa?sinai)?=2i(e?b?eb)cosa?(e?b+eb)sinai?=c?21?(eb?e?b)cosai+21?(e?b+eb)sina=c=c+0i
? { 1 2 ( e ? b + e b ) sin ? a = c 1 2 ( e b ? e ? b ) cos ? a = 0 \Rightarrow \begin{cases} \frac{1}{2}\left( e^{-b}+e^b \right) \sin a=c\\ \frac{1}{2}\left( e^b-e^{-b} \right) \cos a=0\\ \end{cases} ?{21?(e?b+eb)sina=c21?(eb?e?b)cosa=0?
- 当 b = 0 b=0 b=0 时, sin ? a = c \sin a=c sina=c 不成立(所设 a , b ∈ R a,b\in \mathbb{R} a,b∈R)
- 当 cos ? a = 0 \cos a=0 cosa=0 时, 1 2 ( e ? b + e b ) = ± c ? 1 + e 2 b ± 2 c e b = 0 \frac{1}{2}\left( e^{-b}+e^b \right) =\pm c\Rightarrow 1+e^{2b}\pm 2ce^b=0 21?(e?b+eb)=±c?1+e2b±2ceb=0
设 u = e b > 0 u=e^b>0 u=eb>0 ,则有: u = ± c ± c 2 ? 1 u=\pm c\pm \sqrt{c^2-1} u=±c±c2?1?
∴ b = ln ? ( c ± c 2 ? 1 ) \therefore b=\ln \left( c\pm \sqrt{c^2-1} \right) ∴b=ln(c±c2?1?)
? z = π 2 + 2 k π + ln ? ( c ± c 2 ? 1 ) i = π 2 + 2 k π + ln ? ( 2 ± 3 ) i \Rightarrow z=\frac{\pi}{2}+2k\pi +\ln \left( c\pm \sqrt{c^2-1} \right) i=\frac{\pi}{2}+2k\pi +\ln \left( 2\pm \sqrt{3} \right) i ?z=2π?+2kπ+ln(c±c2?1?)i=2π?+2kπ+ln(2±3?)i
8. Ch0-8Matlab/Simulink传递函数Transfer Function

L
?
1
[
a
0
Y
(
s
)
+
s
Y
(
s
)
]
=
L
?
1
[
b
0
U
(
s
)
+
b
1
s
U
(
s
)
]
?
a
0
y
(
t
)
+
y
˙
(
t
)
=
b
0
u
(
t
)
+
b
1
u
˙
(
t
)
?
y
˙
?
b
1
u
˙
=
b
0
u
?
y
\mathcal{L} ^{-1}\left[ a_0Y\left( s \right) +sY\left( s \right) \right] =\mathcal{L} ^{-1}\left[ b_0U\left( s \right) +b_1sU\left( s \right) \right] \\ \Rightarrow a_0y\left( t \right) +\dot{y}\left( t \right) =b_0u\left( t \right) +b_1\dot{u}\left( t \right) \\ \Rightarrow \dot{y}-b_1\dot{u}=b_0u-y
L?1[a0?Y(s)+sY(s)]=L?1[b0?U(s)+b1?sU(s)]?a0?y(t)+y˙?(t)=b0?u(t)+b1?u˙(t)?y˙??b1?u˙=b0?u?y


9. Ch0-9阈值选取-机器视觉中应用正态分布和6-sigma
5M1E——造成产品质量波动的六因素
人 Man Manpower
机器 Machine
材料 Material
方法 Method
测量 Measurment
环境 Envrionment
DMAIC —— 6σ管理中的流程改善
定义 Define
测量 Measure
分析 Analyse
改善 Improve
控制 Control
随机变量与正态分布 Normal Distribution
X
=
(
μ
,
σ
2
)
X=\left( \mu ,\sigma ^2 \right)
X=(μ,σ2)
μ
\mu
μ : 期望(平均值),
σ
2
\sigma ^2
σ2:方差

6σ与实际应用


本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!