基础数据结构第九期 堆（数组+STL）

前言

堆是一种重要的数据结构，因此应该熟练掌握。

一、堆的基本概念

堆的基本：

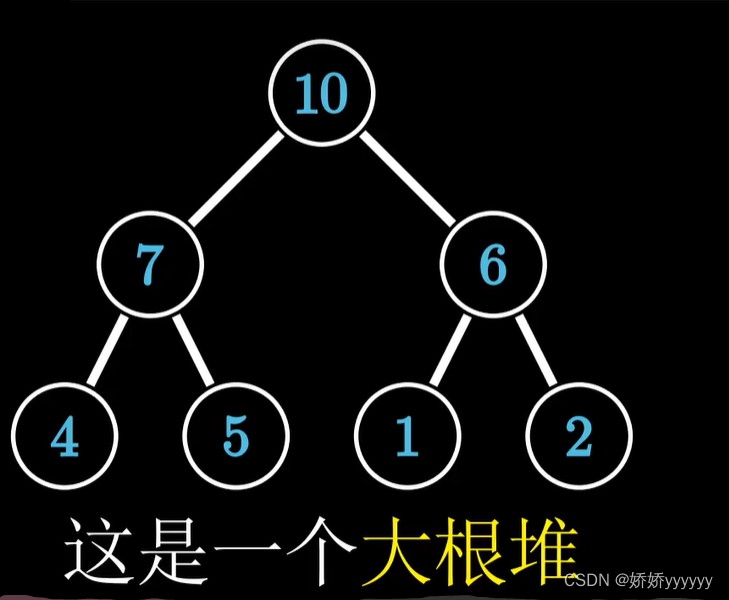
堆的结构实际上是一棵完全二叉树，堆可以分为大根堆和小根堆

大根堆：

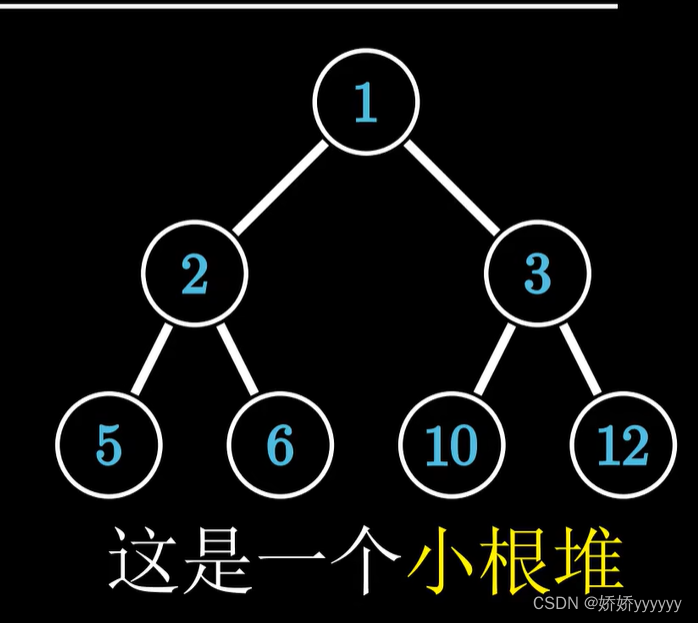
小根堆：

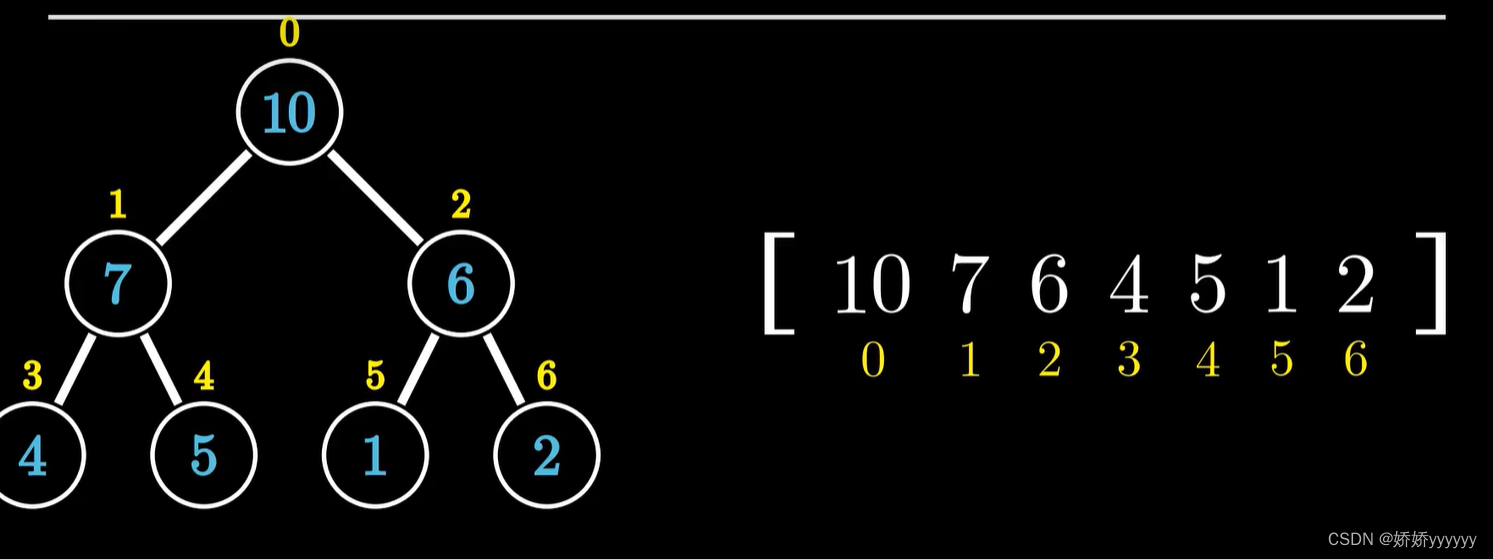
堆的储存：

若节点小标为i，则左子节点下标为2i+1，右子节点下标为2i+2。

堆的基本操作（模板）：

//down模板：

#include<bits/stdc++.h>
using namespace std;
const int N=100010;
int h[N],siz;
int n,m;
void down(int x)
{
? ? int t=x;
? ? if(2*x<=siz && h[2*x]<h[t]) t=2*x;
? ? if(2*x+1<=siz && h[2*x+1]<h[t]) t=2*x+1;
? ? if(x!=t)
? ? {
? ? ? ? swap(h[x],h[t]);
? ? ? ? down(t);
? ? }
}

//up模板：

void up(int x)
{
? ? while(x/2 &&h[x]<h[x/2])
? ? {
? ? ? ? headswap(x/2,x);
? ? ? ? x/=2;
? ? }

STL：

定义大根堆：

#include<iostream>
#include<queue>
using namespace std;
priority_queue<int, vector<int>, less<int> >q;
int main(){
	q.push(1);
	q.push(2);
	cout<<q.top();
	return 0;
}

或：

#include<iostream>
#include<queue>
using namespace std;
priority_queue<int>q;
int main(){
	q.push(1);
	q.push(2);
	cout<<q.top();
	return 0;
}

定义小根堆：

#include<iostream>
#include<queue>
using namespace std;
priority_queue<int, vector<int>, greater<int> >q;
int main(){
	q.push(1);
	q.push(2);
	cout<<q.top();
	return 0;
}

二、典型例题

1.例题：

2.AC代码：

#include <iostream>
#include <algorithm>
#include <string.h>
using namespace std;
const int N = 100010;
int h[N];//堆
int ph[N], hp[N];
int siz;
void heap_swap(int a,int b) {
	swap(ph[hp[a]],ph[hp[b]]);
	swap(hp[a],hp[b]);
	swap(h[a],h[b]);
}

void down(int u) {
	int t = u;
	if (u * 2 <= siz && h[u * 2] < h[t]) {
		t = u * 2;//比左儿子
	}
	if (u * 2 + 1 <= siz && h[u * 2 + 1] < h[t]) {
		t = u * 2 + 1;//比右儿子
	}
	if (u != t) {
		heap_swap(u, t);
		down(t);
	} 
}

void up(int u) {
	while (u / 2 && h[u / 2] > h[u]) {
		heap_swap(u / 2, u);
		u /= 2;
	}
}

int main () {
	int n, m = 0;
	scanf("%d", &n);
	while (n --) {
		char op[10];
		int k, x;
		scanf("%s", op);
		if (!strcmp(op,"I")) {
			scanf("%d", &x);
			siz++;
			m++;
			ph[m] = siz, hp[siz] = m;
			h[siz] = x;
			up(siz);
		}
		else if (!strcmp(op,"PM")) {
			printf("%d\n", h[1]);
		}
		else if (!strcmp(op,"DM")) {
			heap_swap(1, siz);
			siz--;
			down(1);
		}
		else if (!strcmp(op,"D")) {
			scanf("%d", &k);
			k = ph[k];
			heap_swap(k, siz);
			siz--;
			down(k), up(k);
		}
		else {
			scanf("%d%d", &k, &x);
			k = ph[k];
			h[k] = x;
			down(k), up(k);
		}
	}
	return 0;
}

总结：堆在算法中经常用到，应该熟练掌握，感谢大家的观看！！！