冬至·特辑:Note4---二叉树的链式结构

目录
前言🧶
上篇博客,我们学习了二叉树和堆的概念和结构,以及如何实现堆,和堆的应用。有需要的小伙伴可以点击下方链接:
Note3---初阶二叉树~~-CSDN博客文章浏览阅读770次,点赞43次,收藏27次。这篇博客,我们一起来了解并学习数据结构中的初阶的二叉树的概念和性质;以及堆和堆堆应用二叉树的知识点和内容比较多,友友们一定要有耐心看完(跳到自己需要的部分也是OK的)。
https://blog.csdn.net/2301_79184587/article/details/135033457本篇博客,小江带领大家一起学习如何实现二叉树的链式结构+二叉树的性质总结+涉及上篇博客和这篇博客的知识点一些选择题来巩固基础
下面我们就开始今天的学习吧!
1. 二叉树链式结构的实现🐧
1.1 要实现的目标🎯
1.实现二叉树的创建(手动创建)
2.实现二叉树的前序、中序、后序遍历
3.获取二叉树的节点、叶子节点个数
4.获取二叉树的高度
5.获取二叉树的第k层的节点个数
6.查找二叉树中值为x的节点
7.实现二叉树的层序遍历
8.判断是否是完全二叉树
9.实现二叉树的销毁
2.二叉树的创建🌹
???????在学习二叉树的基本操作前,需先要创建一棵二叉树,然后才能学习其相关的基本操作。由于现在大家对二叉树结构掌握还不够深入,为了降低大家学习成本,此处手动快速创建一棵简单的二叉树,快速进入二叉树操作学习,等二叉树结构了解的差不多时,我们反过头再来研究二叉树真正的创建方式。
2.1代码实现
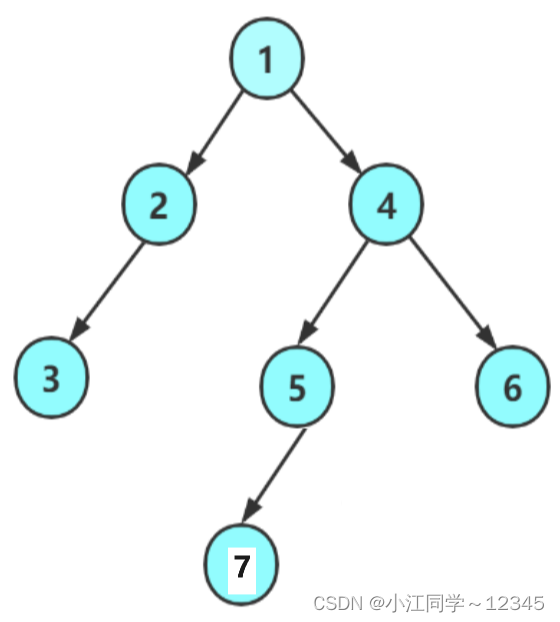
这是我们要实现的二叉树的图(也可以自定义):
从概念中可以看出,二叉树定义是递归式的,因此后序基本操作中基本都是按照该概念实现的。
2.1.1 TreeNode.h
#pragma once
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>
#include<math.h>
typedef int DataType;
typedef struct TreeNode
{
//值 左子树 右子树
DataType data;
struct TreeNode* left;
struct TreeNode* right;
}TNode;
//手动创建一个简单的二叉树
TNode* CreatTree();2.1.2 TreeNode.c
#include"TreeNode.h"
//手动创建一个简单的二叉树
TNode* BuyNode(DataType x)
{
TNode* node = (TNode*)malloc(sizeof(TNode));
if (node == NULL)
{
perror("malloc error!\n");
exit(0);
}
node->data = x;
node->left = node->right = NULL;
return node;
}
TNode* CreatTree()
{
TNode* node1 = BuyNode(1);
TNode* node2 = BuyNode(2);
TNode* node3 = BuyNode(3);
TNode* node4 = BuyNode(4);
TNode* node5 = BuyNode(5);
TNode* node6 = BuyNode(6);
TNode* node7 = BuyNode(7);
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
node5->left = node7;
return node1;
}3.实现二叉树的遍历🐲
所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉树中的节点进行相应的操作,并且每个节点只操作一次。
访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。
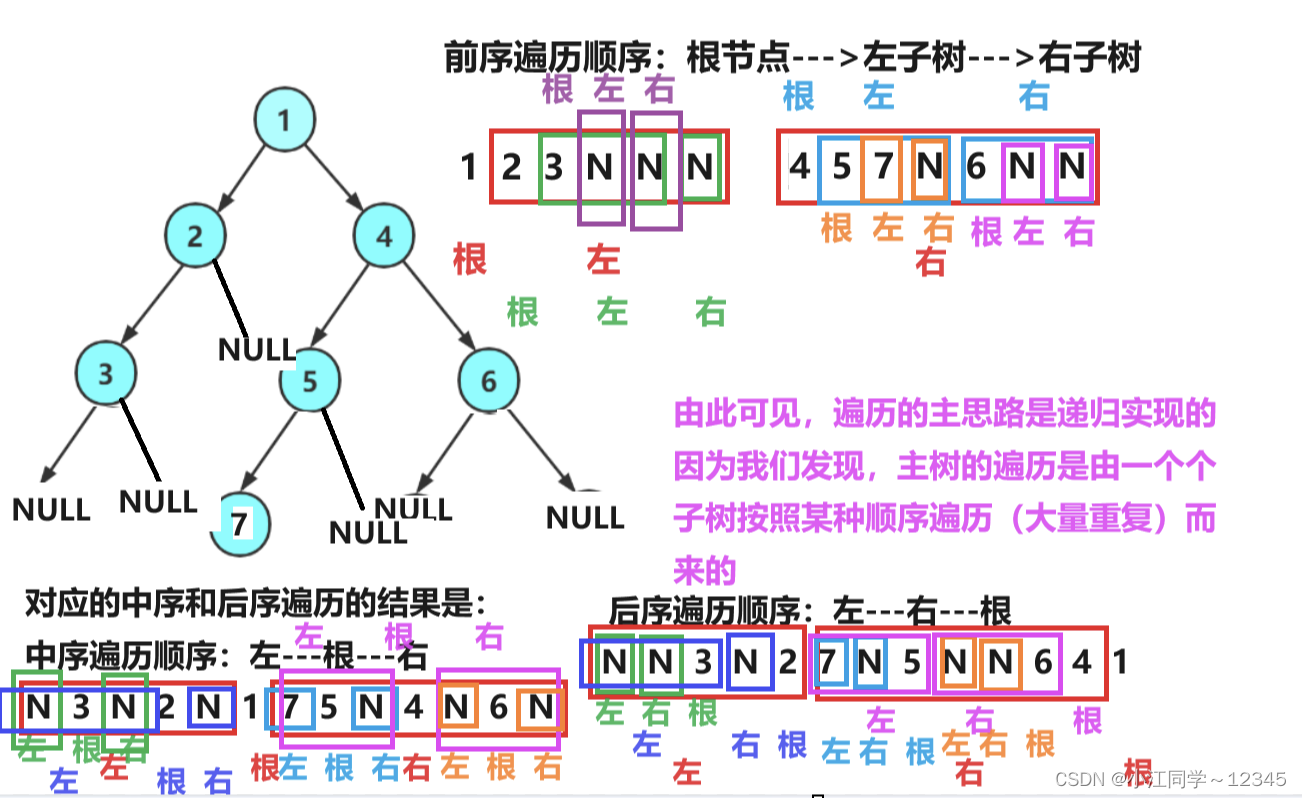
按照规则,二叉树的遍历有:前序/中序/后序的递归结构遍历
前序:根节点--->左子树--->右子树
中序:左子树--->根节点--->右子树
后序:左子树--->右子树--->根节点
3.1 思路分析🐤
下面主要分析前序递归遍历,中序与后序图解类似,大家可自己动手绘制。
3.2?前/中/后序遍历🦦
3.2.1 TreeNode.h
// 二叉树前序遍历
void PreOrder(TNode* root);
// 二叉树中序遍历
void InOrder(TNode* root);
// 二叉树后序遍历
void PostOrder(TNode* root);3.2.2 TreeNode.c
// 二叉树前序遍历
void PreOrder(TNode* root)
{
//注意判空
if (root == NULL)
{
printf("N ");
return;
}
printf("%d ", root->data);
PreOrder(root->left);
PreOrder(root->right);
}
// 二叉树中序遍历
void InOrder(TNode* root)
{
//注意判空
if (root == NULL)
{
printf("N ");
return;
}
InOrder(root->left);
printf("%d ", root->data);
InOrder(root->right);
}
// 二叉树后序遍历
void PostOrder(TNode* root)
{
//注意判空
if (root == NULL)
{
printf("N ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->data);
}3.2.3 test.c
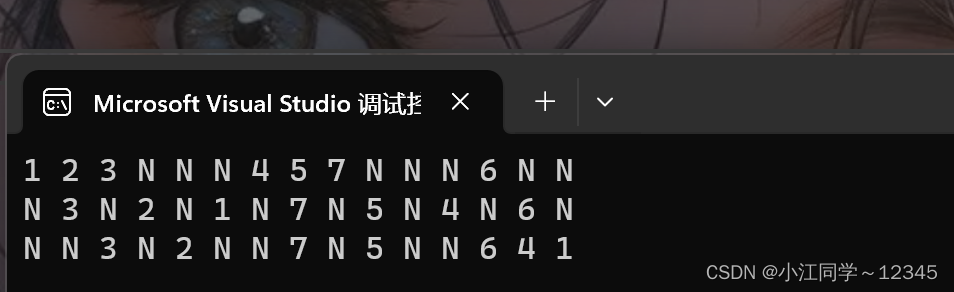
#include"TreeNode.h"
int main()
{
TNode* root=CreatTree();
PreOrder(root);
printf("\n");
InOrder(root);
printf("\n");
PostOrder(root);
printf("\n");
return 0;
}
3.3 递归流程图🐌
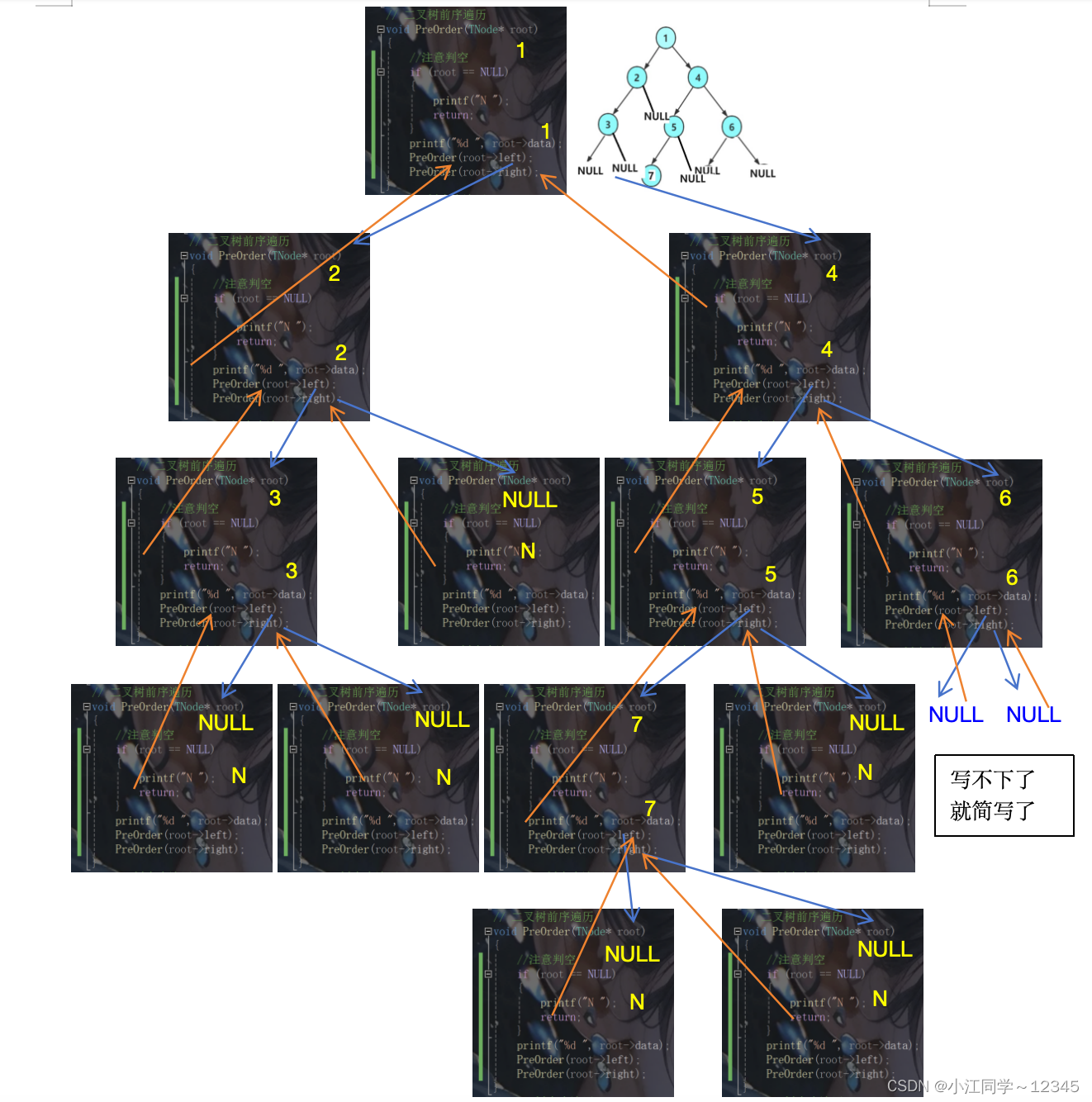
4.获取二叉树的节点、叶子节点个数🦄
4.1 思路分析🙊
总思想:递归+分治
1.求节点个数
分治:左子树节点个数+右子树节点个数+1(根节点)?
2.求叶子节点(无孩子节点)个数
分治:左子树叶子节点个数+右子树叶子节点个数
返回条件:
1. 空 返回0
2. 叶子节点 返回1
?
问题:空树怎么办? 要判断然后直接返回0
4.2 代码实现🦐
4.2.1 TreeNode.h
//节点个数
int TreeSize(TNode* root);
//叶子节点个数
int TreeLeafSize(TNode* root);4.2.2 TreeNode.c
//节点个数
int TreeSize(TNode* root)
{
if (root == NULL)
return 0;
return TreeSize(root->left) + TreeSize(root->right) + 1;
}
//叶子节点个数
int TreeLeafSize(TNode* root)
{
//空树,返回0
if (root == NULL)
return 0;
//叶子节点,返回1
if (root->left == NULL && root->right == NULL)
return 1;
return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}4.2.3 test.c
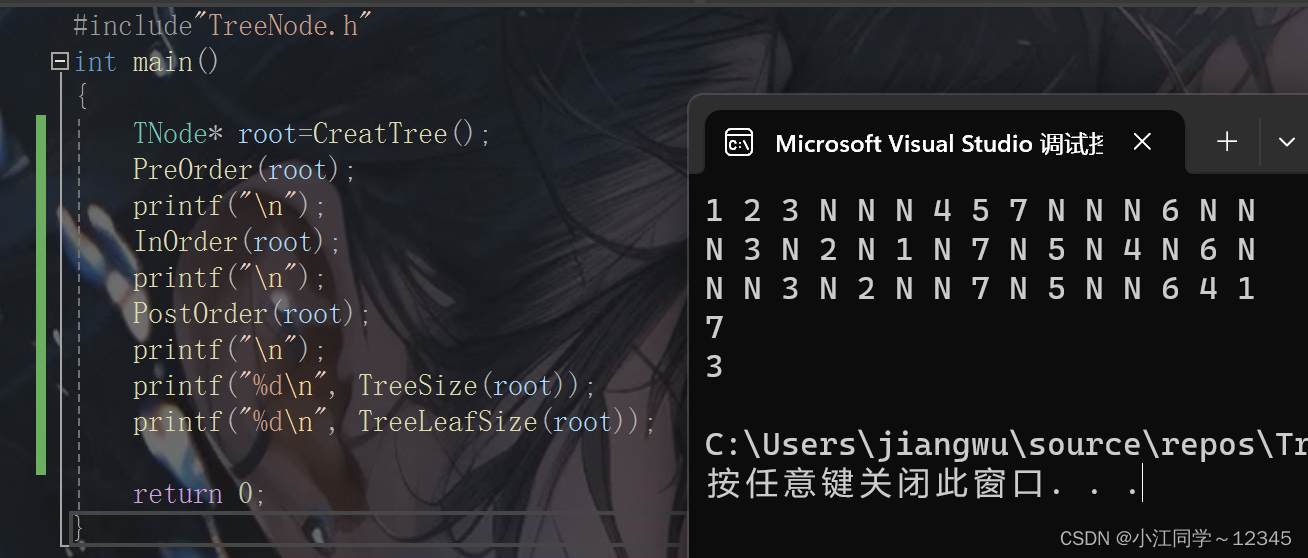
4.3 递归流程图🍄
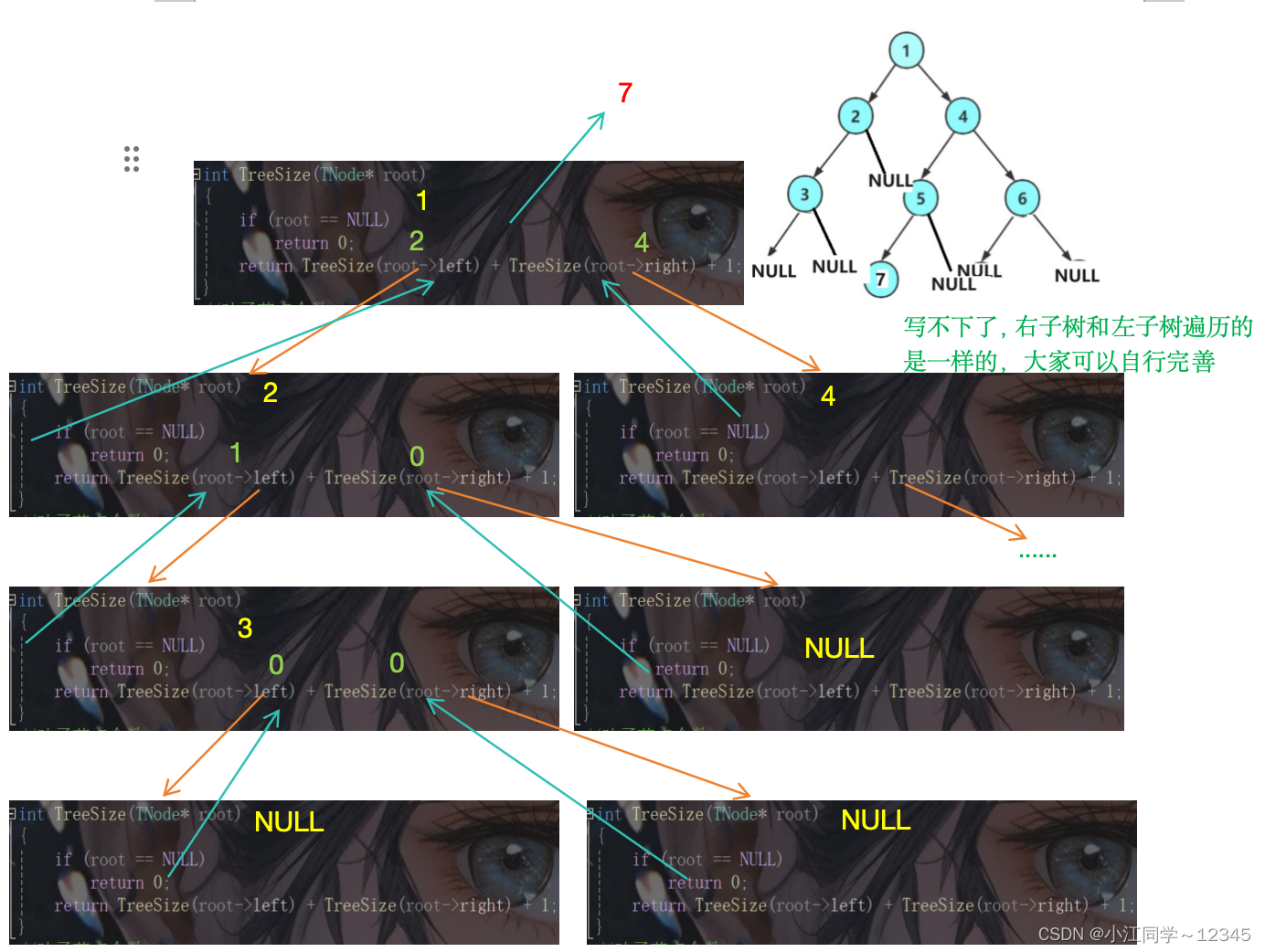
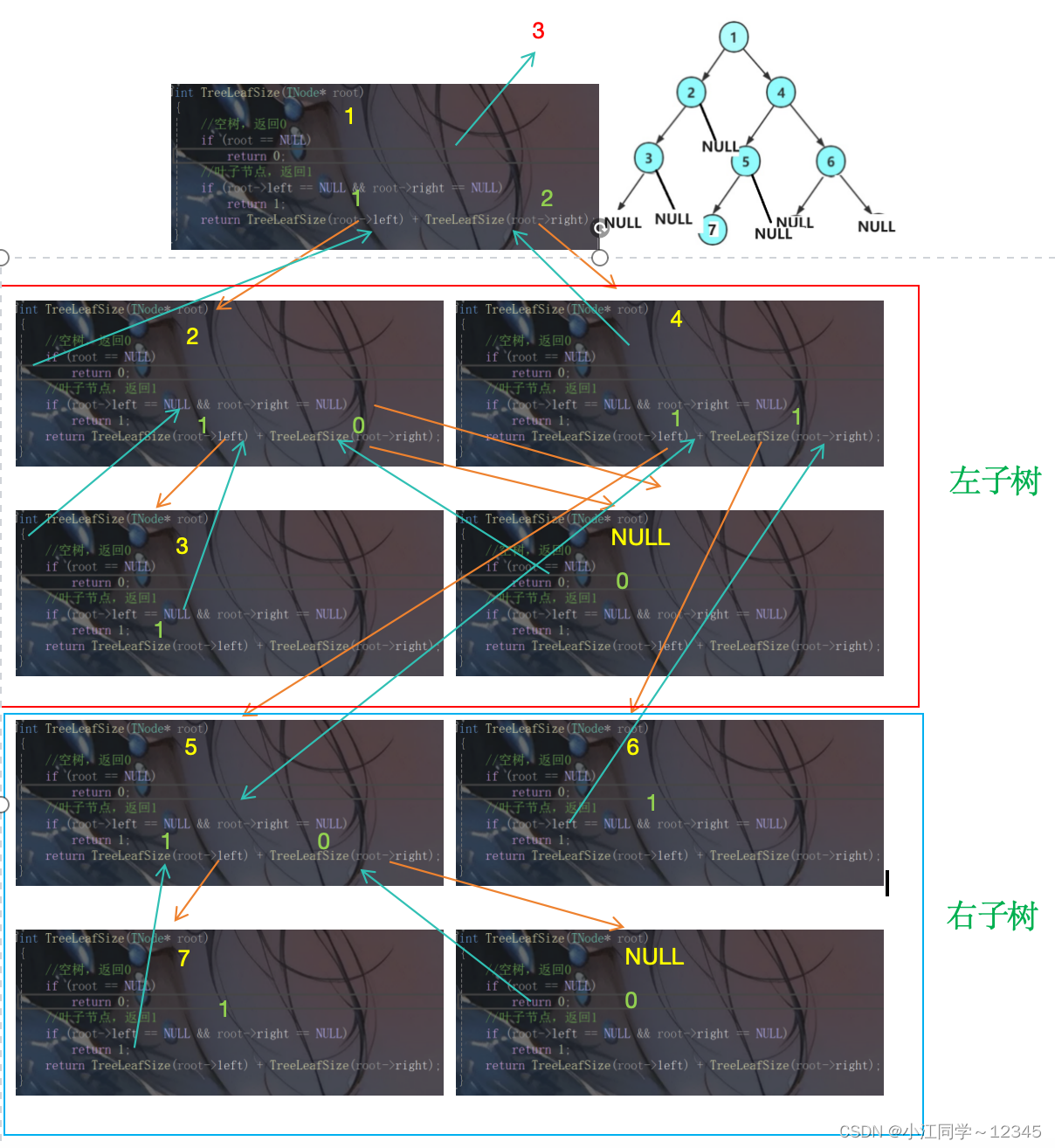
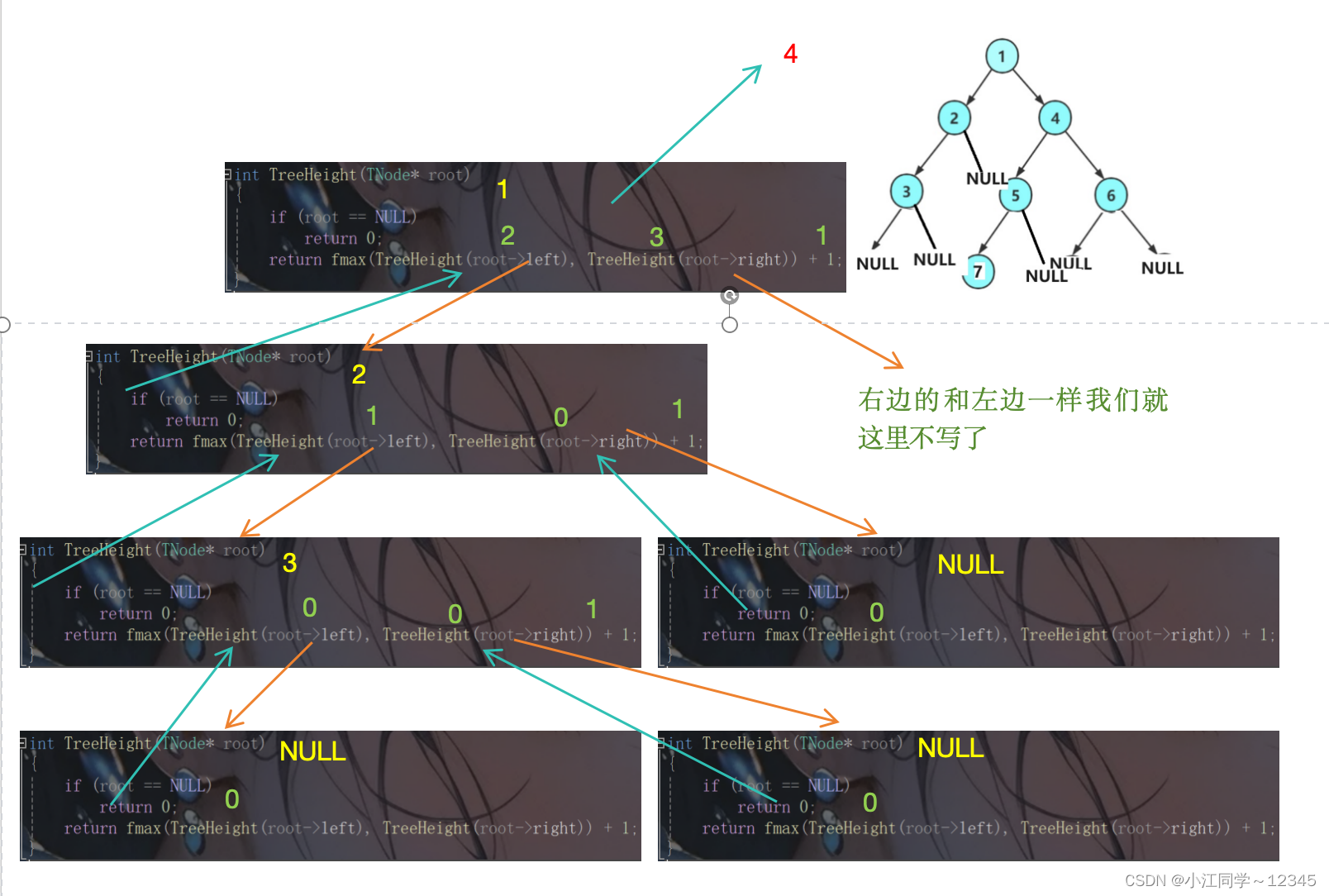
5.获取二叉树的高度🦁
5.1 思路分析🌵
递归+分治:
1.空?返回0
2.非空 比较左子树和右子树高度 较大的+1并且返回
5.2 代码实现🍀

5.2.1 TreeNode.h
//求高度
int TreeHeight(TNode* root);5.2.2 TreeNode.c
//求高度
int TreeHeight(TNode* root)
{
if (root == NULL)
return 0;
return fmax(TreeHeight(root->left), TreeHeight(root->right)) + 1;
}5.2.3 test.c
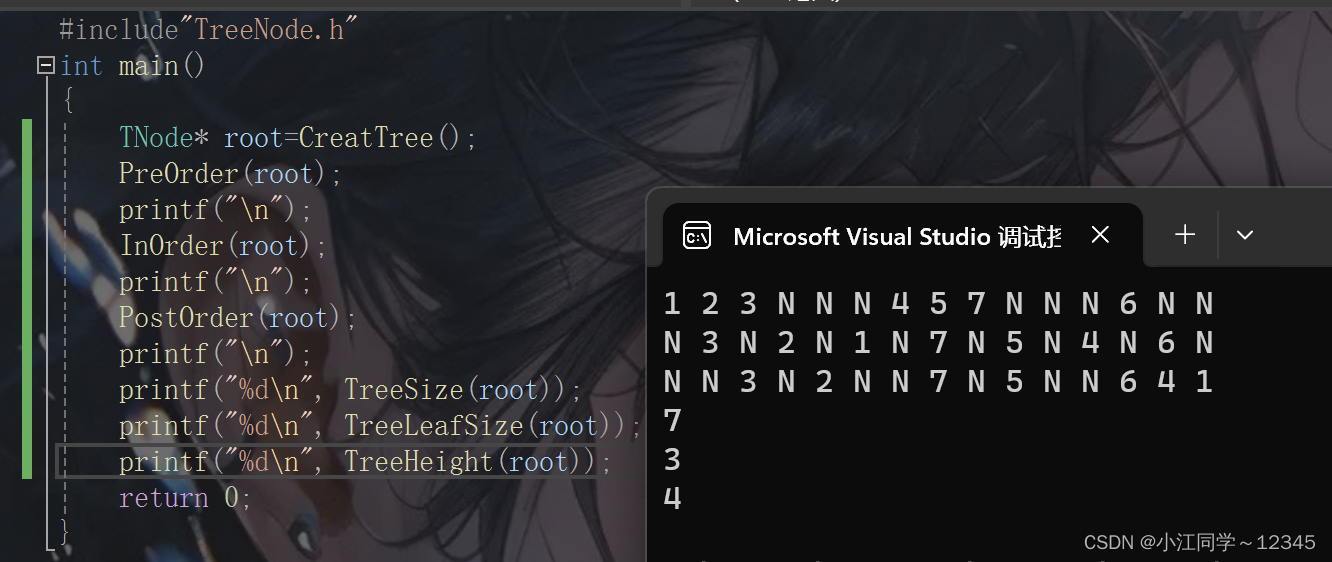
5.3 递归流程图🌼
6.求二叉树的第k层的节点个数🐙
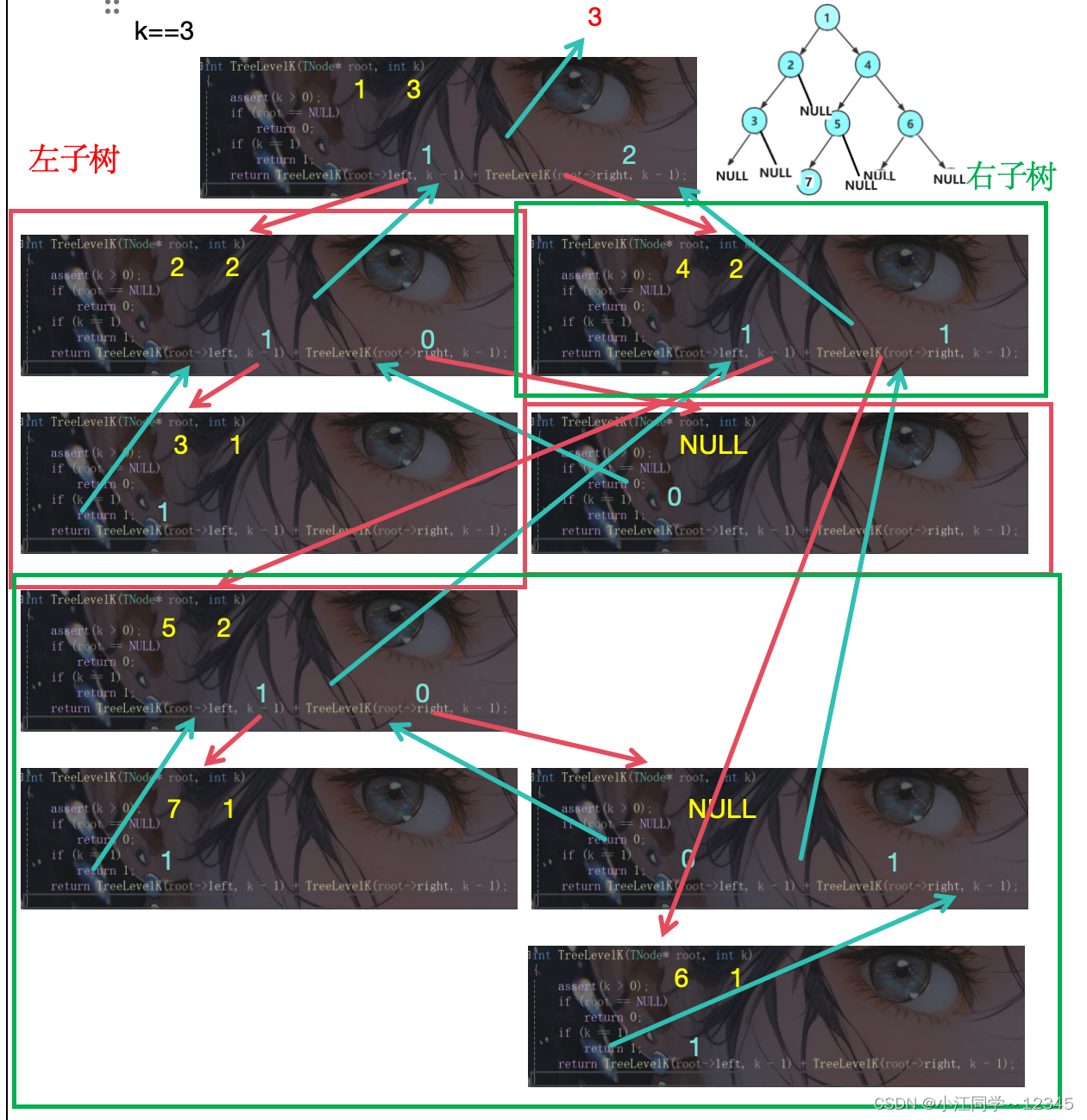
6.1 思路分析🦤
递归+分治:
1. 为空 返回0
2. 不为空并且k==1(根节点那一层) 返回1
3. 不为空并且k>1 返回左子树(k-1)层总个数+右子树(k-1)总层个数(不包括第一层)
6.2 代码实现🌾
6.2.1 TreeNode.h
//求第k层节点个数
int TreeLevelK(TNode* root, int k);6.2.2 TreeNode.c
//求第k层节点个数
int TreeLevelK(TNode* root, int k)
{
assert(k > 0);
if (root == NULL)
return 0;
if (k == 1)
return 1;
return TreeLevelK(root->left, k - 1) + TreeLevelK(root->right, k - 1);
}6.2.3 test.c
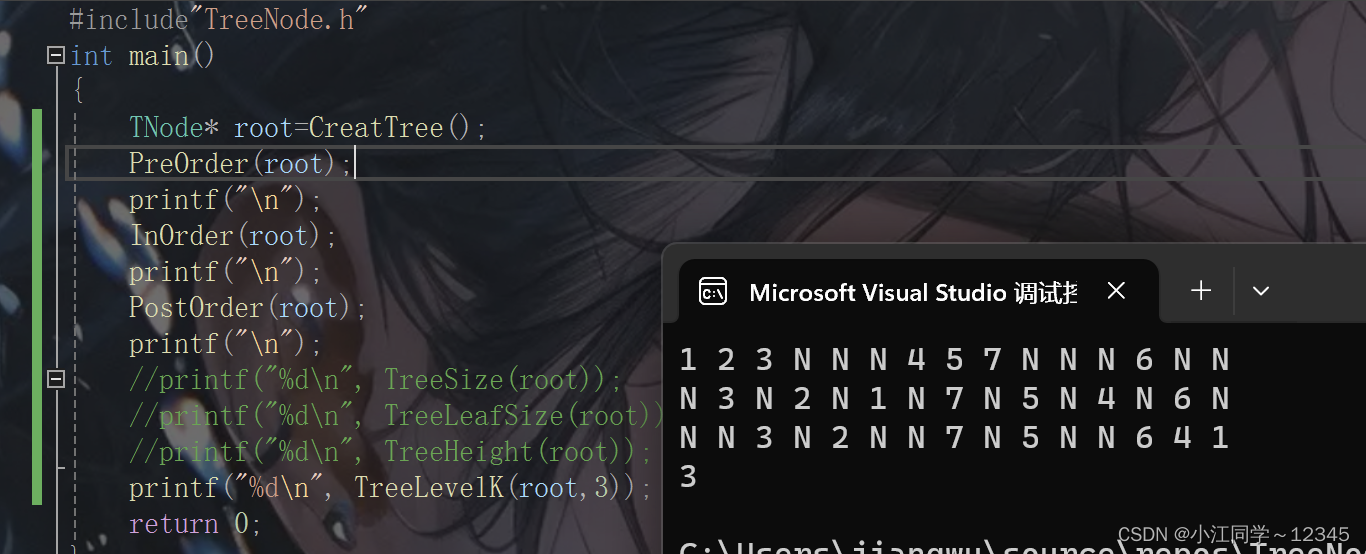
6.3 递归流程图🍁
7.查找二叉树中值为x的节点🐨
7.1 思路分析🌻
递归+分治:
1.空 ?返回NULL
2.值==x ?返回节点
3.值!=x ?先左子树遍历,比较+记录 ? 左子树没找到,右子树遍历,比较+遍历
7.2 代码实现🪺
7.2.1 TreeNode.h
//求x的节点
TNode* TreeFind(TNode* root, DataType x);7.2.2 TreeNode.c
//求x的节点
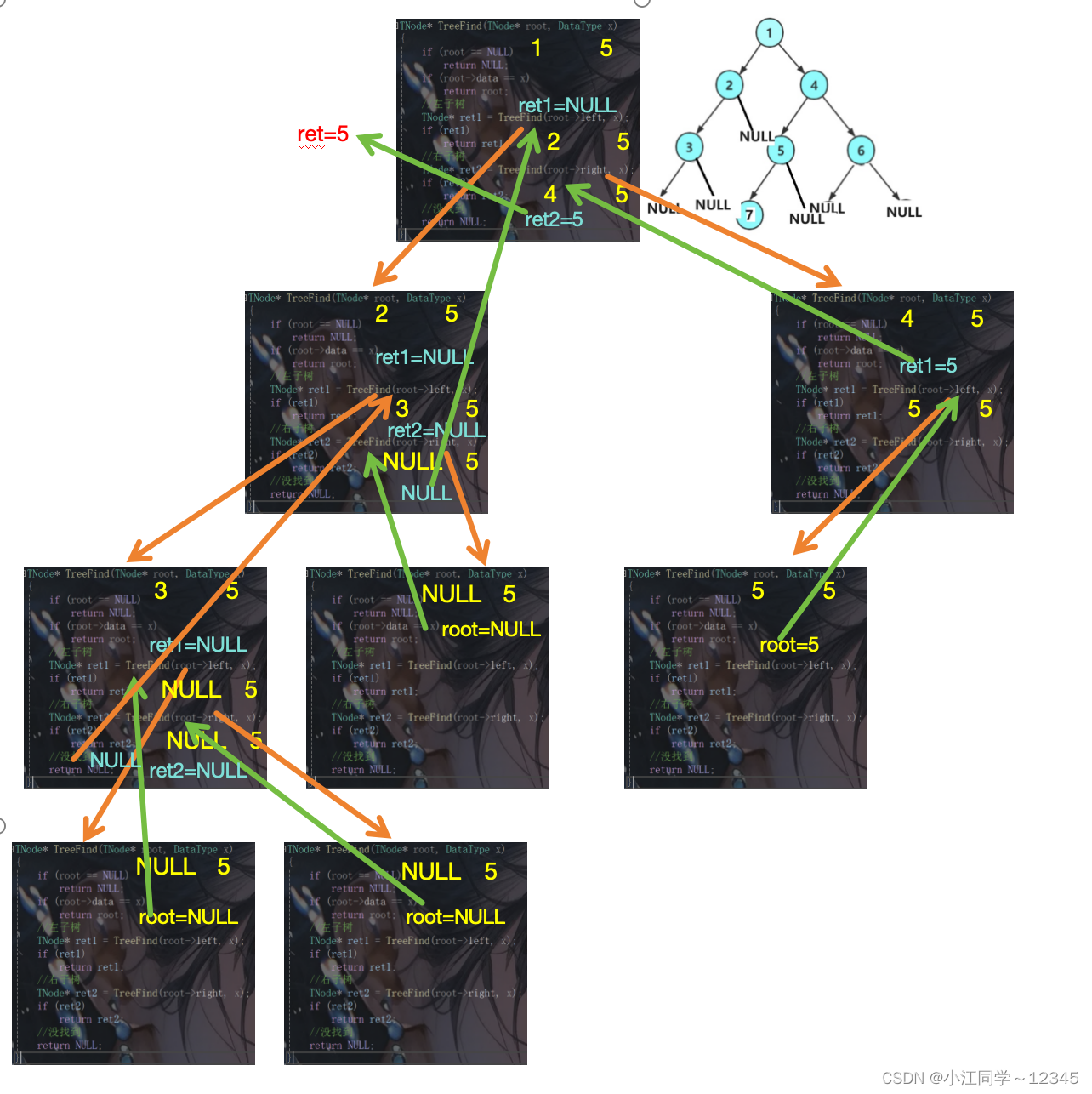
TNode* TreeFind(TNode* root, DataType x)
{
if (root == NULL)
return NULL;
if (root->data == x)
return root;
//左子树
TNode* ret1 = TreeFind(root->left, x);
if (ret1)
return ret1;
//右子树
TNode* ret2 = TreeFind(root->right, x);
if (ret2)
return ret2;
//没找到
return NULL;
}7.2.3 test.c
7.3 递归流程图🎄
8.实现二叉树的层序遍历🐝
1.什么是层序遍历?
一层一层遍历二叉树
?
2.层序遍历为什么要单独拿出来讲,而不是和前/中/后序一起讲?
因为层序遍历不需要递归就能实现,但是需要借助队列实现
?
3.为什么要借助队列实现?
因为队列的性质是先进先出,符合二叉树遍历的要求(遍历完一层,就打印一层的内容)
?
4.队列存放节点还是节点的值?
存放节点,因为单独存放值的话,找不到它的左孩子和右孩子?
5.队列放节点还是节点的指针呢?
节点的指针--->方便查找--->注意修改的Queue.h中QDataType的类型,不再是int类型的值了
8.1 思路分析🐚
1. 根节点入队
2.队列不为空的话:
获取头节点--->出队--->打印--->左子树入队--->右子树入队(一层就入队完成了)
继续循环??一层一层出
3.队列为空:
循环结束---遍历结束
8.2 代码实现🥊
队列的代码在之前的博客有,这里就不再做解释了,需要的小伙伴点击下方链接:
8.2.1 TreeNode.h
//层序遍历
void LevelOrder(TNode* root);8.2.2 TreeNode.c
//层序遍历
void LevelOrder(TNode* root)
{
Queue q;
QueueInit(&q);//初始化
if (root)
QueuePush(&q, root);
int LevelSize = 1;
while (!QueueEmpty(&q))
{
//一层一层出
while (LevelSize--)
{
TNode* front = QueueFront(&q);
QueuePop(&q);
printf("%d ", front->data);
//下一层的左子树
if (front->left)
QueuePush(&q, front->left);
//下一层的右子树
if (front->right)
QueuePush(&q, front->right);
}
printf("\n");
LevelSize = QueueSize(&q);
}
printf("\n");
QueueDestroy(&q);
}8.2.3 Queue.h
#pragma once
#include"TreeNode.h"
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
// 链式结构:表示队列
typedef struct TreeNode* QDataType;
typedef struct QListNode
{
struct QListNode* _next;
QDataType _data;
}QNode;
// 队列的结构
typedef struct Queue
{
QNode* _head;
QNode* _tail;
int size;
}Queue;
// 初始化队列
void QueueInit(Queue* q);
// 队尾入队列
void QueuePush(Queue* q, QDataType data);
// 队头出队列
void QueuePop(Queue* q);
// 获取队列头部元素
QDataType QueueFront(Queue* q);
// 获取队列队尾元素
QDataType QueueBack(Queue* q);
// 获取队列中有效元素个数
int QueueSize(Queue* q);
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
int QueueEmpty(Queue* q);
// 销毁队列
void QueueDestroy(Queue* q);8.2.4 Queue.c
#include"Queue.h"
// 初始化队列
void QueueInit(Queue* q)
{
assert(q);
q->_head = q->_tail = NULL;
q->size = 0;
}
// 队尾入队列
void QueuePush(Queue* q, QDataType data)
{
assert(q);
QNode* node = (QNode*)malloc(sizeof(QNode));
if (node == NULL)
{
perror("malloc error!\n");
return;
}
node->_data = data;
node->_next = NULL;
if (q->_head == NULL)
{
q->_head = q->_tail = node;
}
else
{
q->_tail->_next = node;
q->_tail = node;
}
q->size++;
}
// 队头出队列
void QueuePop(Queue* q)
{
assert(q);
//不为空
assert(q->_head);
//只有1给节点,直接free
if (q->_head->_next == NULL)
{
free(q->_head);
q->_head = NULL;
}
else
{
QNode* del = q->_head;
q->_head = q->_head->_next;
free(del);
del = NULL;
}
q->size--;
}
// 获取队列头部元素
QDataType QueueFront(Queue* q)
{
assert(q);
assert(q->_head);
return q->_head->_data;
}
// 获取队列队尾元素
QDataType QueueBack(Queue* q)
{
assert(q);
assert(q->_tail);
return q->_tail->_data;
}
// 获取队列中有效元素个数
int QueueSize(Queue* q)
{
assert(q);
return q->size;
}
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
int QueueEmpty(Queue* q)
{
assert(q);
if (q->_head == NULL)
return 1;
return 0;
}
// 销毁队列
void QueueDestroy(Queue* q)
{
assert(q);
QNode* del = q->_head;
while (del)
{
QNode* next = del->_next;
free(del);
del = NULL;
del = next;
}
q->_head = q->_tail = NULL;
q->size = 0;
}8.2.5?test.c
8.3 代码中存在的困惑点🔥
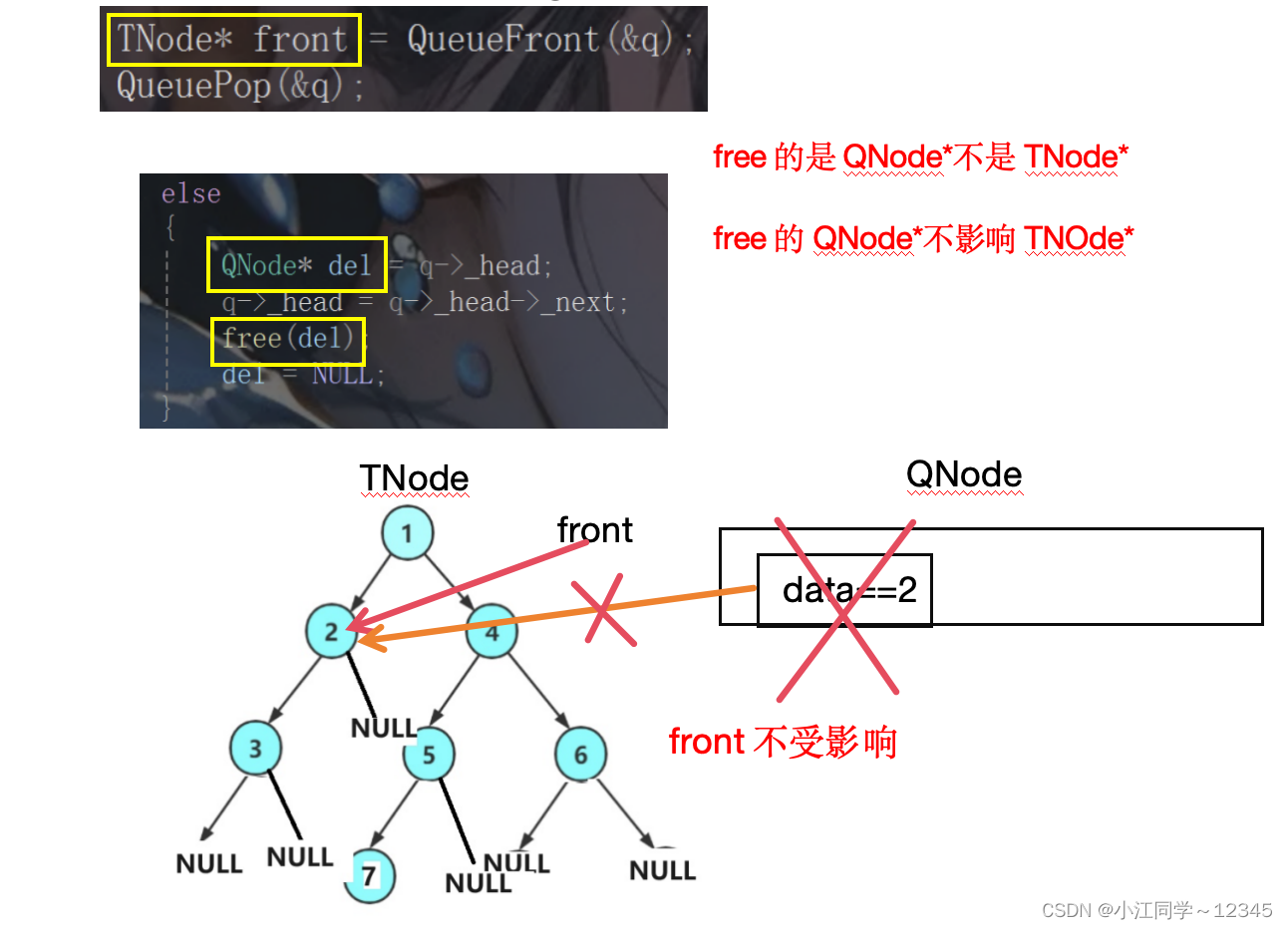
1.?front不是free了吗,还能使用吗?为什么?
2.为什么队列中的有效个数(k)就代表是第k层?
因为获取到该层的头节点时,头节点的下一层左右子树不为空的节点会存储到队列里面,当该层的节点都出队之后,下一层的全部节点也已经入队
此时队里面只有下一层的节点个数,要知道LevelSize代表的是内循环次数,此时队里面有K个节点,出队K次刚刚好
9.判断是否是完全二叉树🐠
9.1 思路分析🥟
关键点---只要不连续就不是完全二叉树---依据层序遍历的基础上实现
怎么判断是否连续?
层序遍历遍历到空结束,判断后面是否为空,为空则为完全二叉树;非空则不是完全二叉树
???????注意??
不存在空已经进去了的情况,但是后面的非空还没进去的情况(可以自己尝试举例看看)
9.2 代码实现🍿
9.2.1 TreeNode.h
//判断是否是完全二叉树
bool TreeComplete(TNode* root);9.2.2 TreeNode.c
//判断是否是完全二叉树
bool TreeComplete(TNode* root)
{
Queue q;
QueueInit(&q);//初始化
if (root)
QueuePush(&q, root);
int LevelSize = 1;
while (!QueueEmpty(&q))
{
TNode* front = QueueFront(&q);
QueuePop(&q);
//判空
if (front == NULL)
break;
QueuePush(&q, front->left);
QueuePush(&q, front->right);
}
//遇到空之后,判别后面是否为空
while (!QueueEmpty(&q))
{
TNode* front = QueueFront(&q);
QueuePop(&q);
if (front)
{
QueueDestroy(&q);
return false;
}
}
QueueDestroy(&q);
return true;
}9.2.3 tets.c
?
10.实现二叉树的销毁🪼
10.1 思路分析🧋
1. 用什么顺序遍历二叉树?
后序遍历
因为后序遍历,不用考虑左右子树的保存,更加方便
当然,前/中序也可以写
?
前序首先会free根节点,这就需要保存左右子树,否则找不到左右子树
中序会在free完左子树之后,free根节点,这就需要保存右子树,否则找不到右子树
后序最后才free根节点
2. 用一级指针还是二级指针?
一级指针,前面我们说过最好保证指针级数一致,但是一级指针需要手动置空
10.2 代码实现🧁
10.2.1 TreeNode.h
//销毁
void DestroyTree(TNode* root);10.2.2 TreeNode.c
//销毁
void DestroyTree(TNode* root)
{
if (root == NULL)
return;
//后序
DestroyTree(root->left);
DestroyTree(root->right);
free(root);
}10.2.3 test.c
#include"TreeNode.h"
#include"Queue.h"
int main()
{
TNode* root=CreatTree();
PreOrder(root);
printf("\n");
InOrder(root);
printf("\n");
PostOrder(root);
printf("\n");
//printf("%d\n", TreeSize(root));
//printf("%d\n", TreeLeafSize(root));
//printf("%d\n", TreeHeight(root));
//printf("%d\n", TreeLevelK(root,3));
//TNode* ret = TreeFind(root, 5);
//printf("TreeFind:%p\n", ret);
/*LevelOrder(root);*/
printf("%d\n", TreeComplete(root));
DestroyTree(root);
root = NULL;
return 0;
}后语🪢
本次的博客,我们介绍了如何实现二叉树的链式结构。下篇博客,我们将一起练习二叉树的知识运用,包含性质题,选择题,oj题。
本次的分享到这里就结束了!!!
PS:小江目前只是个新手小白。欢迎大家在评论区讨论哦!有问题也可以讨论的!
如果对你有帮助的话,记得点赞👍+收藏??+关注?

?
?
?
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!