递归算法:二叉树前序、中序、后序遍历解析与递归思想深度剖析
2023-12-21 12:24:28

文章目录
一、二叉树的遍历
学习二叉树链式结构,最简单的方式就是遍历。所谓 二叉树遍历(Traversal) 是按照某种特定的规则,依次对二叉树中的结点进行相应的操作,并且每个结点只操作一次。
按照规则,二叉树的遍历有:前序/中序/后序的递归结构遍历:
- 前序遍历
( Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。 - 中序遍历
( Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。 - 后序遍历
( Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后
访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。
由于被访问的结点必是某子树的根,所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。
1.1 链式结构二叉树的创建
这里只是模拟创建一下链式二叉树真正的结构并不是这样创建的:
📚 代码演示:
#include<stdio.h>
#include<stdlib.h>
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;
//创建节点
BTNode* BuyNode(int x)
{
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
if (node == NULL)
{
perror("malloc file");
exit(-1);
}
node->data = x;
node->left = NULL;
node->right = NULL;
return node;
}
int main()
{
BTNode* node1 = BuyNode(1);
BTNode* node2 = BuyNode(2);
BTNode* node3 = BuyNode(3);
BTNode* node4 = BuyNode(4);
BTNode* node5 = BuyNode(5);
BTNode* node6 = BuyNode(6);
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
PreOrder(node1);
return 0;
}
1.1 二叉树结构图

二、 前序遍历
前序遍历( Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
- 也就是先访问堆顶然后再访问左子树 (但是要保证每个子树都是这样遍历的)
- 而这个情况用递归在合适不过了,简直就是非常的简单。大家看下这段代码看看理解嘛?
代码演示:
//前序遍历
void PreOrder(BTNode* root)
{
if (root == NULL)
return;
printf("%d ", root->data);
PreOrder(root->left);
PreOrder(root->right);
}
是不是非常震惊,只需要几行代买就解决前序遍历的问题,这就是递归思想
- 大问题化简成递归小问题
🍹递归的技巧
大问题转化为子问题
以及递归的结束条件
2.1 前序遍历递归展开图
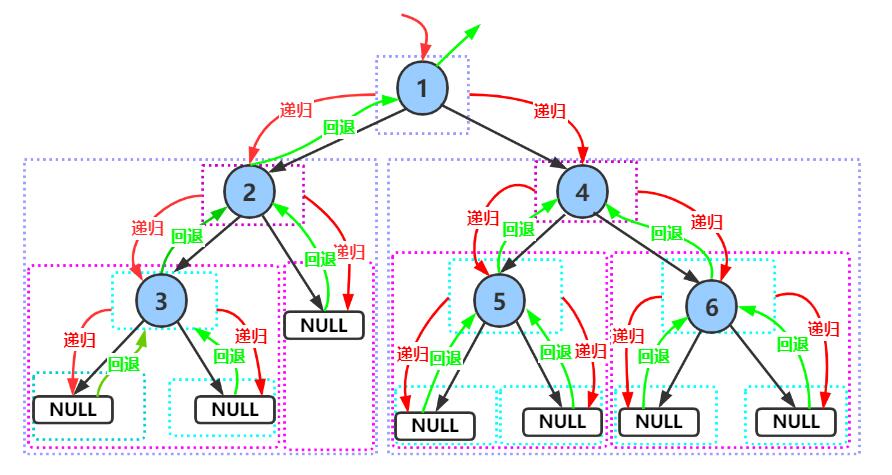
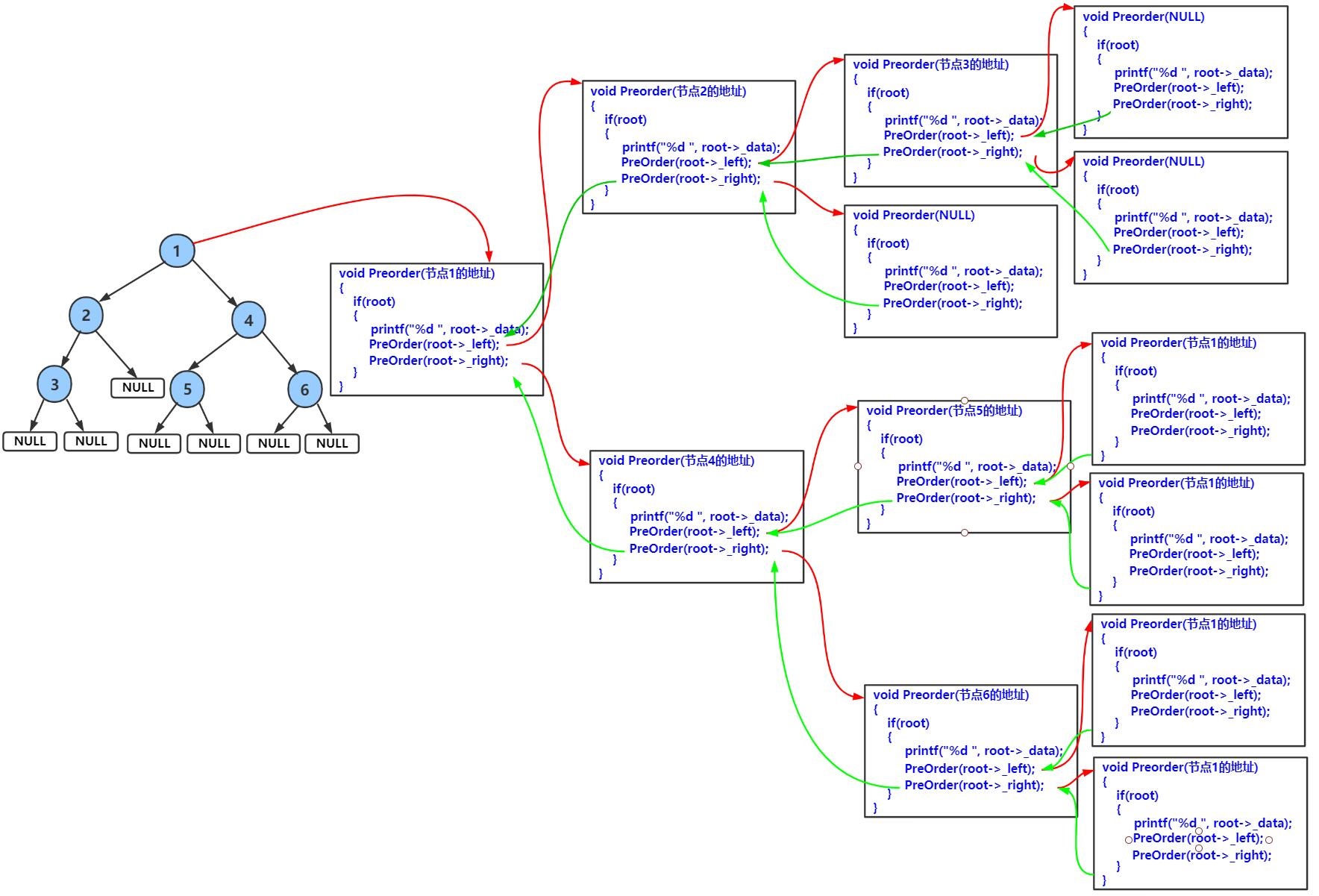
三、中序遍历
有了前序遍历的经验我们接下来中序遍历简直就是 直接秒杀
- 直接照猫画虎就好了
代码演示:
//中序遍历
void InOrder(BTNode* root)
{
if (root == NULL)
return;
InOrder(root->left);
printf("%d ", root->data);
InOrder(root->right);
}
四、后序遍历
代码演示:
//后序遍历
void PostOrder(BTNode* root)
{
if (root == NULL)
return;
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->data);
}
五、二叉树的层序遍历
层序遍历就是从所在二叉树的根结点出发,首先访问第一层的树根结点,然后从左到右访问第2层上的结点,接着是第三层的结点.
- 以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。

5.1 层序遍历的思想
层序遍历大家看到一层一层遍历不知道对,我们前面学的数据结构 队列 是否有想法也是和层序一样:
- 从跟进去然后是左右子树,子树又是左右子树
- 每次把根 打印出来就把他的子树带进去 然后删除跟
- 这样是不是就是前一层带后一层的子树了
📚 代码演示:
// 层序遍历
void LevelOrder(BTNode* root)
{
Que q;
QueueInit(&q);
if (root)
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
printf("%d ", front->data);
if(front->left)
QueuePush(&q, front->left);
if (front->right)
QueuePush(&q, front->right);
QueuePop(&q);
}
}
📝文章结语:
?? 把本章的内容全部掌握,铁汁们就可以熟练应用switch语句啦!
看到这里了还不给博主扣个:
?? 点赞🍹收藏 ?? 关注!
💛 💙 💜 ?? 💚💓 💗 💕 💞 💘 💖
拜托拜托这个真的很重要!
你们的点赞就是博主更新最大的动力!
有问题可以评论或者私信呢秒回哦。

文章来源:https://blog.csdn.net/qq_57761637/article/details/135103646
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!