2-2基础算法-Nim和/前缀和/差分

一.Nim和

Nim游戏是一个数学策略游戏，通常涉及两名玩家轮流从几堆物品（如石子或饼干）中取走一定数量的物品。每个玩家每次可以从任意一堆中取走任意数量的物品，但必须至少取走一个。最后无法进行操作的玩家输掉游戏。

Nim和是所有堆中物品数量的二进制异或（XOR）结果。在计算Nim和时，我们将每堆物品的数量转换为二进制数，然后对这些二进制数进行异或运算。例如，如果有三堆物品，数量分别是3、5、7，则它们的二进制表示分别是011、101、111。它们的Nim和是011 XOR 101 XOR 111 = 001。

在标准的Nim游戏中，如果Nim和为0，那么当前的局面对于后手（即非当前回合的玩家）是有利的，因为后手可以通过策略性地取物品，始终保持Nim和为0的状态，直到游戏结束。如果Nim和非0，先手（当前回合的玩家）处于优势，因为他们可以通过一次操作改变堆的状态，使Nim和变为0，从而控制游戏进程。

[例] Alice和Bob的爱恨情仇

评测系统

分析：此题游戏规则中有额外的限制（每次只能取走k的奇数倍的物品），我们需要对标准Nim游戏的策略进行调整。我们可以通过检查每堆中物品的数量是否可以通过取走k的奇数倍来减少到Nim和的值，从而确定哪位玩家拥有获胜策略。

#include <iostream>
#include <vector>
using namespace std;
int power(int base, int exp) {
    int result=1;
    while (exp) {
        result = result * base;
        exp--;
    }
    return base;
}
bool canwin(int a[], int n, int k) {
    int nimsum = 0;
    for (int i = 0; i < n; i++) {
        nimsum = nimsum ^ a[i];//异或^
    }
    if (nimsum == 0)
        return false;
    for (int i = 0; i < n; i++) {
        int num = a[i];//第i堆饼干数量
        for (int j = 1; power(j,k) <= num; j+=2) { //保证j是奇数
            if (num - power(j, k) == (nimsum ^ num)) //即:如果if条件满足，那么当前玩家可以通过这次移动使得整个游戏的Nim和变为0
                return true;
        }
    }
    return false;
}
int main()
{
    int n, k;
    cin >> n >> k;
    int a[2000005];
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }
    bool wins = canwin(a, n, k);
    cout<<(wins ? "Alice" : "Bob");
}

二.前缀和&区间和

1.前缀和原理和特点
定义：（类似于前n项和）
prefix[0]=0

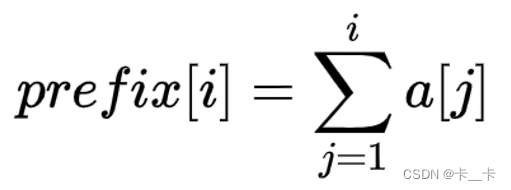
性质：

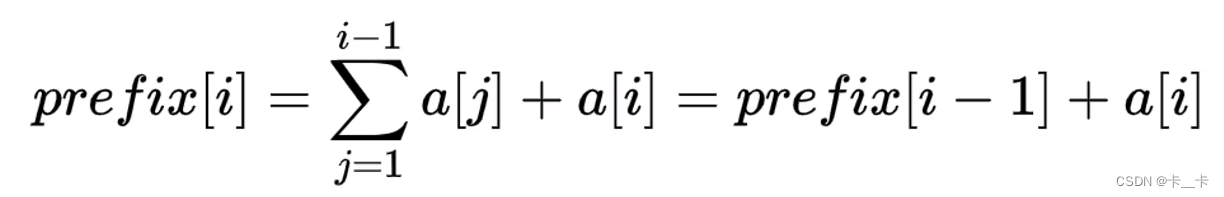
前缀和可以在O(1)的复杂度处理一段区间的和
如：数组l到r的和，等于p[r]-p[l-1]

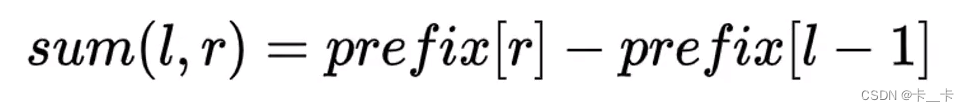
2.例题
（1）区间次方和

评测系统

常规方式可能超时

由于k比较小，我们可以定义5个数组，分别表示原数组的1~5次幂，然后只需输出l ~ r之间元素的和即可。整个过程可以借助二维数组实现。此方法仍然会超时

再加上前缀和

#include <iostream>
#include <vector>
using namespace std;
const int value= 1e9+7;
int main()
{
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	int n, m;
	cin >> n >> m;
	long long arr[6][100005];
	for (int i = 1; i <= n; i++) { //输入与k次方
		cin >> arr[1][i];
		for (int k = 2; k <= 5; k++) {
			arr[k][i] = arr[k - 1][i] * arr[1][i]%value;
		}
	}
	long long prefix[6][100005];//前缀和数组
	for (int i = 1; i <= 5; i++) {
		for (int j = 1; j <= n; j++) {
			prefix[i][j] = (prefix[i][j - 1] + arr[i][j]) % value;
		}
	}
	while (m--) {
		int a, b, c;
		cin >> a >> b >> c;
		//在计算过程中对每个元素都取模，会导致后面元素不一定大于前面元素
		//最终结果仍要取模，并考虑负数的出现
		cout << (prefix[c][b]-prefix[c][a-1]+value)%value << endl;
	}
}

（2）大石头的搬运工


评测系统

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
int main()
{
	int n;
	cin >> n;
	pair<int, int> q[N];//初始数据
	for (int i = 1; i <= n; ++i) {
		cin >> q[i].second >> q[i].first;//first初始位置,second权重
	}
	sort(q+1, q + n+1);

	long long s = 0;
	long long prefix[N] = { 0 }; //从第一个位置到位置i的所有石头 移动到位置i的总费用
	for (int i = 1; i <= n; ++i) {
		prefix[i] =prefix[i - 1] + s * (q[i].first - q[i - 1].first);
		s += q[i].second;
	}

	s = 0;
	long long nextfix[N] = { 0 };//从位置i到最后一个位置的所有石头 移动到位置i的总费用
	for (int i = n; i >= 1; --i) {
		nextfix[i] =nextfix[i + 1]+ s * (q[i + 1].first - q[i].first);
		s += q[i].second;
	}

	long long res=1e18;
	for (int i = 1; i <= n; ++i) {
		res = min(res, prefix[i] + nextfix[i]);
	}
	cout << res;
}

（3）最大数组和



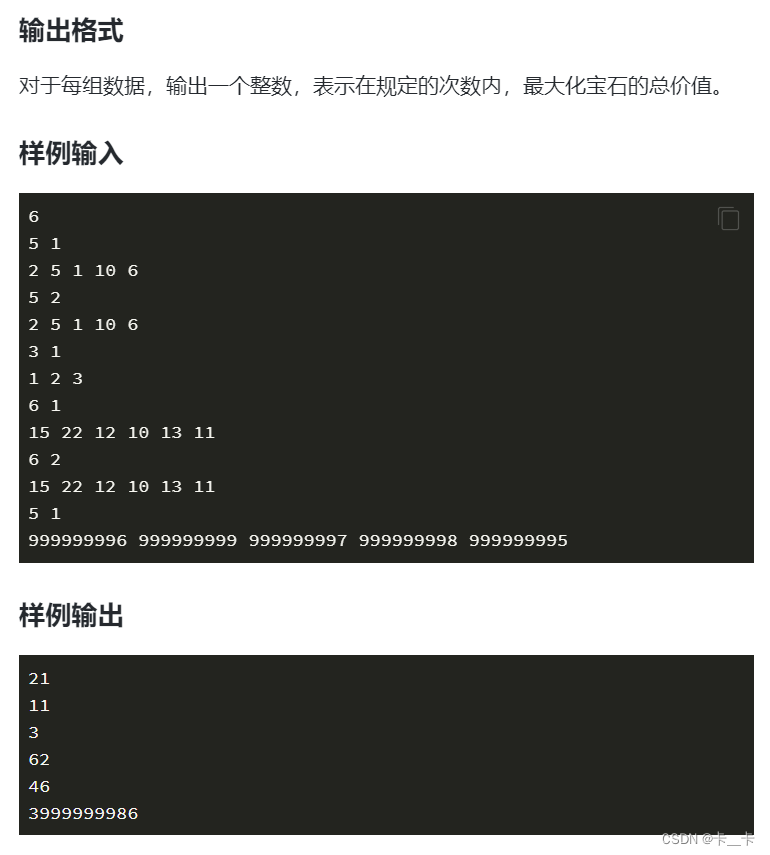
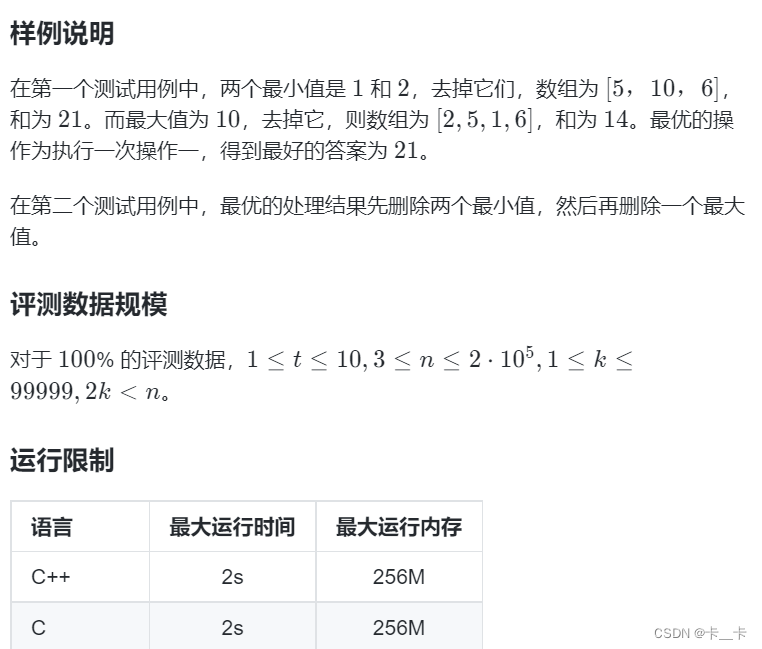
评测系统

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 2e5+5;
int main()
{
	int t;
	cin >> t;
	long long sum;
	while (t--) {
		long long a[N] = { 0 };
		int n, k;
		cin >> n >> k;
		sum = 0;
		for (int i = 1; i <= n; ++i) {
			cin >> a[i];
			sum += a[i];
		}
		sort(a+1, a + n+1);
		long long pre[N] = { 0 }, nex[N] = { 0 };
		for (int i = 1; i <= n; ++i) {//前缀和
			pre[i] = pre[i - 1] + a[i];
		}
		for (int i = n; i >= 1; --i) {//后缀和
			nex[i] = nex[i + 1] + a[i];
		}
		long long temp = 1e18;
		for (int i = 0; i <= k; ++i) {
			int cntmin = i * 2;//对前面处理i次，删掉了开头的2i个数
			int cntmax = k - i;//对后面操作了k-i次，删掉了尾部的k-i个数
			temp=min(temp,pre[cntmin] + nex[n-cntmax+1]);
		}
		cout << sum - temp << endl;
	}
}

三.差分

差分的主要优势是可以快速地对原数组的一个区间内的所有元素进行同样的增加或减少操作。

1.原理
定义：差分定义为原数组相邻元素之间的差值
a[]原数组，diff差分数组
其中diff[0]=a[0]

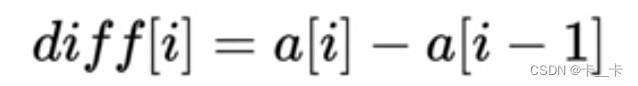
性质：差分数组的前缀和等于原数组

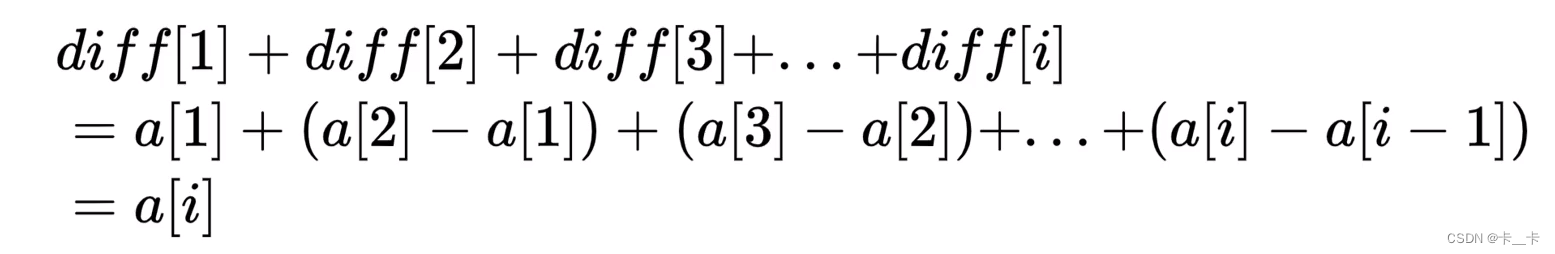
如果我们想对区间[k,r]中的元素都加x
只需：
从k到数组末尾的元素都加x：diff[k]+=x
r+1及其以后的元素都减x：diff[r+1]-=x

这里diff[k]+=x的意义是，a[k]比a[k-1]多了x。a[k+1]和a[k]的差值要想保持不变，也a[k+1]也需要加x，以此类推

注：只有使用前缀和输出才是有效更新

2.练习
（1）区间更新

评测系统

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5 + 5;
int main()
{
	int n, m;
	while (cin >> n >> m) {
		int a[N] = { 0 }, diff[N] = { 0 }, prefix[N] = { 0 };
		for (int i = 1; i <= n; i++) {
			cin >> a[i];
		}
		for (int i = 1; i <= n; i++) {
			diff[i] = a[i] - a[i - 1];
		}
		while (m--) {
			int x, y, z;
			cin >> x >> y >> z;
			diff[x] += z;
			diff[y+1] -= z;
		}
		for (int i = 1; i <= n; i++) { //使用前缀和还原
			prefix[i] = prefix[i - 1] + diff[i];
		}
		for (int i = 1; i <= n; i++) {
			cout << prefix[i] << " ";
		}
		cout << endl;
	}
}

（2）小明的彩灯

评测系统

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 5e5 + 5;  //修改
int main()
{
	int n, q;
	cin >> n >> q;
	long long a[N] = { 0 }, diff[N] = { 0 }, prefix[N] = { 0 };  //修改
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
	}
	for (int i = 1; i <= n; i++) {
		diff[i] = a[i] - a[i - 1];
	}
	while (q--) {
		int x, y, z;
		cin >> x >> y >> z;
		diff[x] += z;
		diff[y + 1] -= z;
	}
	for (int i = 1; i <= n; i++) {
		prefix[i] = prefix[i - 1] + diff[i];
	}
	for (int i = 1; i <= n; i++) {  //修改
		if (prefix[i] > 0)
			cout << prefix[i] << " ";
		else
			cout << 0 <<" ";
	}
	cout << endl;
}