【数据结构】——排序篇（中）

前面我们已经了解了几大排序了，那么我们今天就来再了解一下剩下的快速排序法，这是一种非常经典的方法，时间复杂度是N*logN。

快速排序法：

基本思想为：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

我们的快速排序可以通过递归和非递归来实现，我们先来看看递归实现快排，我们的递归快排又分为三个版本，三种方法各有各的特点，我们接下来就来看看吧。

需要调用的函数代码：

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

int GetMidi(int* a, int begin, int end)
{
	int midi = (begin + end) / 2;
	// begin midi end 三个数选中位数
	if (a[begin] < a[midi])
	{
		if (a[midi] < a[end])
			return midi;
		else if (a[begin] > a[end])
			return begin;
		else
			return end;
	}
	else // a[begin] > a[midi]
	{
		if (a[midi] > a[end])
			return midi;
		else if (a[begin] < a[end])
			return begin;
		else
			return end;
	}
}

hoare版本单趟排序：

// hoare
int PartSort1(int* a, int begin, int end)
{
	int midi = GetMidi(a, begin, end);
	Swap(&a[midi], &a[begin]);

	int left = begin, right = end;
	int keyi = begin;

	while (left < right)
	{
		// 右边找小
		while (left < right && a[right] >= a[keyi])
		{
			--right;
		}

		// 左边找大
		while (left < right && a[left] <= a[keyi])
		{
			++left;
		}

		Swap(&a[left], &a[right]);
	}

	Swap(&a[left], &a[keyi]);

	return left;
}

这个版本的单趟排序理解起来很容易，但是我们的坑点比较多，所以难度对于我们而言还是有点挑战性，我们需要两个变量来实现，我们的left从左边数组的首元素开始走，找比keyi位置大的元素，keyi代表的就是我们数组首元素的下标，我们用right从最后一个元素开始走，找比keyi位置小的元素，找到了一个大的元素和一个小的元素就交换，但是我们的数组中可能有多个相等的元素，所以我们内嵌循环就得用<=。我们最后left和right相遇时结束，相遇位置的右边的元素大于等于keyi位置的元素，而相遇位置左边的元素都小于等于keyi位置的元素，我们最后就将left位置的元素和keyi位置的元素交换再返回left就完成了。

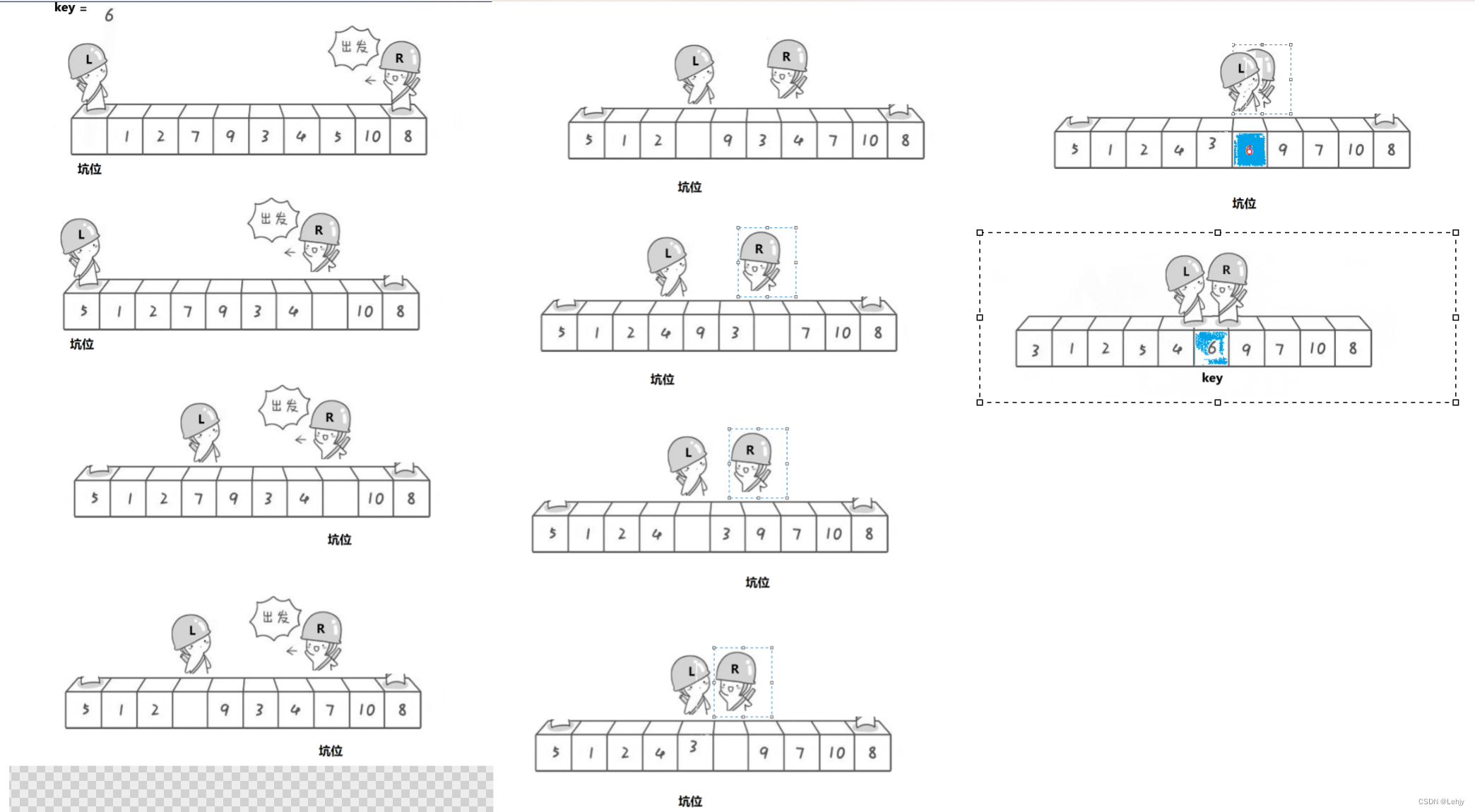
挖坑法单趟排序：

int PartSort2(int* a, int begin, int end)
{
	int midi = GetMidi(a, begin, end);
	Swap(&a[midi], &a[begin]);

	int key = a[begin];
	int hole = begin;
	while (begin < end)
	{
		// 右边找小，填到左边的坑
		while (begin < end && a[end] >= key)
		{
			--end;
		}

		a[hole] = a[end];
		hole = end;

		// 左边找大，填到右边的坑
		while (begin < end && a[begin] <= key)
		{
			++begin;
		}

		a[hole] = a[begin];
		hole = begin;
	}

	a[hole] = key;
	return hole;
}

我们先将第一个数据存放在临时变量key中形成一个坑位，我们同样用到left和right，同样的用法，left从第一个元素往后走，right从最后一个元素往前走。我们的right先走，找到一个比hole下标小的元素就于hole下标的元素交换，交换之后left再走，找到一个比hole位置大的元素就与hole位置的元素交换，然后再left位置形成一个坑点。然后又是right走，交换后left走，反复进行，最后在相遇的时候就结束循环。因为我们的hole下标的值都是空的，所以在最后我们将key的数据给hole下标的坑位就可以了，最后再返回坑位的数据。具体的过程如下图所示：

前后指针版本单趟排序：

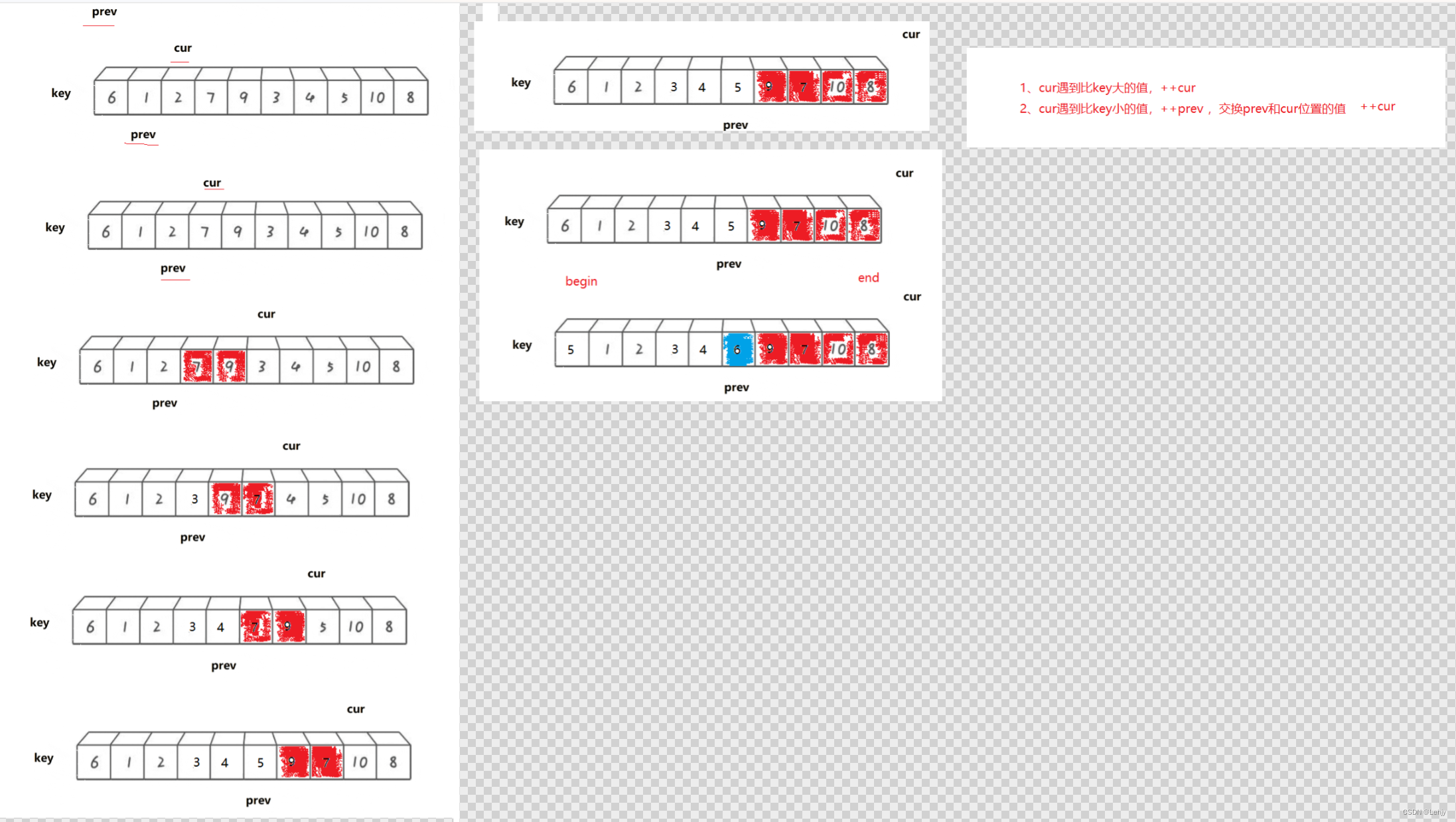
int PartSort3(int* a, int begin, int end)
{
	int midi = GetMidi(a, begin, end);
	Swap(&a[midi], &a[begin]);
	int keyi = begin;

	int prev = begin;
	int cur = prev + 1;
	while (cur <= end)
	{
		if (a[cur] < a[keyi] && ++prev != cur)
			Swap(&a[prev], &a[cur]);

		++cur;
	}

	Swap(&a[prev], &a[keyi]);
	keyi = prev;
	return keyi;
}

我们的前后指针版本看起来比前两个版本更加的容易，因为我们的两个指针prev指向我们数组首元素的下标，而cur是我们首元素的下一个元素的下标，我们的cur先走，如果我们指向的元素比keyi位置的元素大的话我们就cur++向前走一位，如果比keyi位置的元素小的话我们就prev++向前走一位再与cur位置的交换，cur再继续往前走知道cur>end的时候就结束循环。最后我们再将prev位置的数据给keyi位置就完成了。

单趟优化版本：

void QuickSort(int* a, int begin, int end)
{
	if (begin >= end)
		return;

	if (end - begin + 1 <= 10)
	{
		InsertSort(a + begin, end - begin + 1);
	}
	else
	{
		int midi = GetMidi(a, begin, end);
		Swap(&a[midi], &a[begin]);

		int left = begin, right = end;
		int keyi = begin;

		while (left < right)
		{
			// 右边找小
			while (left < right && a[right] >= a[keyi])
			{
				--right;
			}

			// 左边找大
			while (left < right && a[left] <= a[keyi])
			{
				++left;
			}

			Swap(&a[left], &a[right]);
		}

		Swap(&a[left], &a[keyi]);
		keyi = left;

		// [begin, keyi-1] keyi [keyi+1, end]
		QuickSort(a, begin, keyi - 1);
		QuickSort(a, keyi + 1, end);
	}
}

单趟优化版本就是我们的区间数据不大时，我们用直接插入排序法，而数据太大的时候我们就用hoare版本的单趟排序。

函数递归实现快排：

void QuickSort(int* a, int begin, int end)
{
	if (begin >= end)
		return;

	int keyi = PartSort2(a, begin, end);
	QuickSort(a, begin, keyi - 1);
	QuickSort(a, keyi + 1, end);
}

实现我们只需要调用一个版本的单趟排序在进行递归就可以了。我们代码中是用的挖坑法的单趟排序，我们就直接调用PartSort2就可以了。

递归的我们已经了解完了，那么我们就来看看非递归的怎么实现吧：

void QuickSortNonR(int* a, int begin, int end)
{
	ST s;
	STInit(&s);
	STPush(&s, end);
	STPush(&s, begin);

	while (!STEmpty(&s))
	{
		int left = STTop(&s);
		STPop(&s);
		int right = STTop(&s);
		STPop(&s);

		int keyi = PartSort3(a, left, right);
		// [left, keyi-1] keyi [keyi+1, right]
		if (left < keyi - 1)
		{
			STPush(&s, keyi - 1);
			STPush(&s, left);
		}

		if (keyi + 1 < right)
		{
			STPush(&s, right);
			STPush(&s, keyi + 1);
		}
	}

	STDestroy(&s);
}

非递归版本的快速排序。我们需要起始位置 begin 和结束位置 end。首先，函数创建一个栈 st，用于存储待处理的子数组的起始和结束位置。将 end 和 begin 分别压入栈中，表示对整个数组进行排序。进入循环，只要栈不为空，从栈中弹出两个元素，分别赋值给 left 和 right，表示当前要处理的子数组的起始和结束位置。调用 PartSort3 函数对子数组进行分区，得到基准元素的位置 keyi。根据分区的结果，将子数组划分为 [left, keyi-1]、[keyi]、[keyi+1, right] 三个部分。如果 keyi + 1 < right，说明右侧子数组仍然有元素需要排序，将右侧子数组的起始位置 keyi + 1 和结束位置 right 压入栈中。如果 left < keyi - 1，说明左侧子数组仍然有元素需要排序，将左侧子数组的起始位置 left 和结束位置 keyi - 1 压入栈中。循环继续进行，直到栈为空，表示所有子数组都被处理完毕。最后，销毁栈 st，就完成了非递归版本的快速排序。

如果对大家有所帮助的话就支持一下吧！