DL Homework 11

2023-12-25 10:14:08

目录

1. 被优化函数??编辑?(代码来源于邱锡鹏老师的神经网络与深度学习的实验）

L1.py

op.py

（1）SimpleBatchGD

（2）Adagrad

（3）RMSprop

（4）Momentum

（5）Adam

2.被优化函数??编辑?

?3.解释不同轨迹的形成原因，并分析各个算法的优缺点

（1）SimpleBatchGD

（2）Adagrad

（3）RMSprop

（4）Momentum

（5）Adam

总结

在展开本次作业之前，首先要明确优化对于深度学习非常重要

训练更快

? ? ? ? 训练复杂的模型可能需要数小时、几天甚至数周

? ? ? ? 优化算法的性能直接影响模型的训练效率

模型更好

? ? ? ? 了解优化算法的原则及其超参数的作用

? ? ? ? 能够以有针对性的方式调整超参数,提高模型的性能

高纬变量的非凸优化

鞍点（saddle point）梯度为0，在一些维度上是最高点，在另一些维度上是最低点。既不是全局最小值也不是局部最小值。

驻点（Stationary Point）梯度为0的点，高纬空间中大部分驻点都是鞍点。

高维空间非凸优化的难点：如何逃离鞍点

在梯度方向上引入随机性，可以有效地逃离鞍点

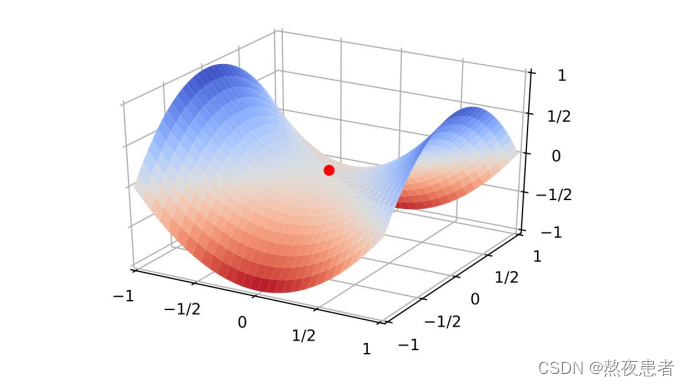
高纬空间的非凸优化问题

模型收敛到平坦局部最小值，鲁棒性会更好，即微小的参数变动不会剧烈影响模型能力；

模型收敛到尖锐局部最小值，鲁棒性会较差

具备良好泛化能力的模型通常应该是鲁棒的，因此理想的局部最小值应该是平坦的

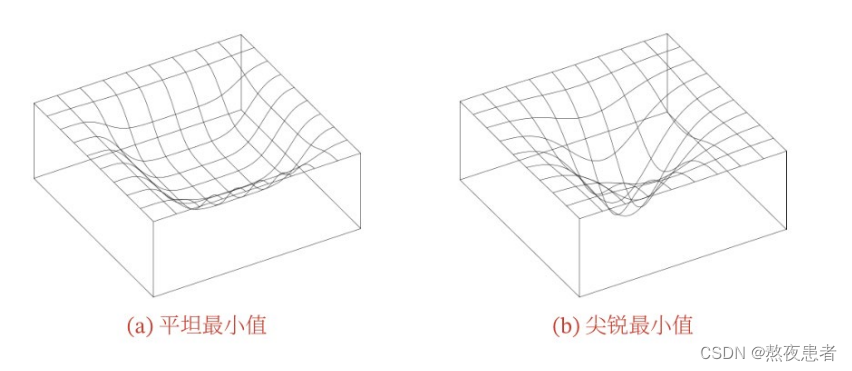
优化算法大体上可以分为两类：

1） 调整学习率， 使得优化更稳定

2） 梯度估计修正， 优化训练速度

简要介绍图中的优化算法，编程实现并2D可视化

1. 被优化函数?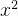x^{2}?(代码来源于邱锡鹏老师的神经网络与深度学习的实验）

期望结果如下：

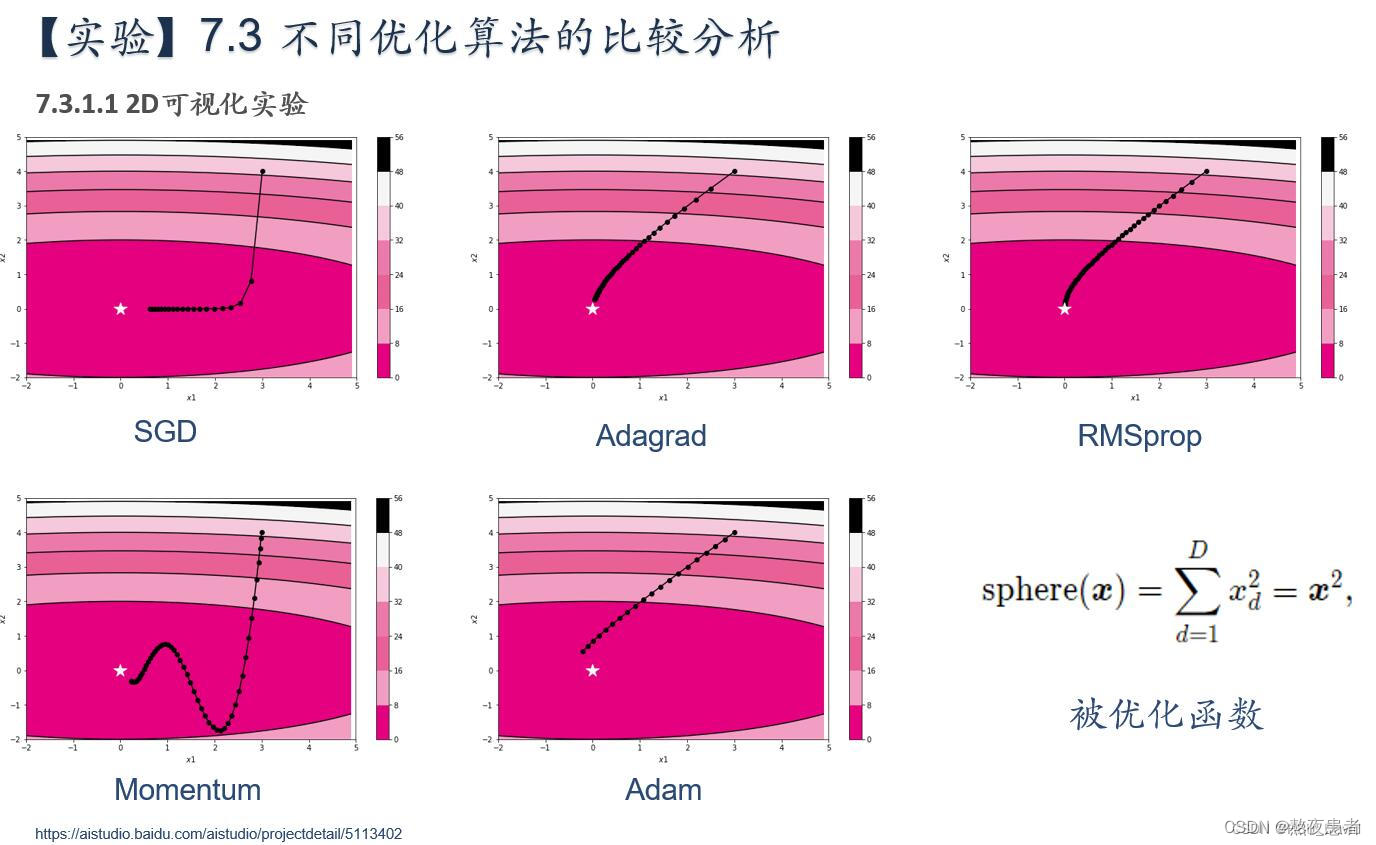
被优化函数选择Sphere函数作为被优化函数，并对比它们的优化效果。Sphere函数的定义为

\mathrm{sphere}(x ) = \sum_{d=1}^{D} x_d^2 = x^2,

其中?$ x \in \mathbb{R}^D$?，?$ x^2$?表示逐元素平方。Sphere函数有全局的最优点?$ x^*=0$。

这里为了展示方便，我们使用二维的输入并略微修改Sphere函数，定义?$\mathrm{sphere}( x) = w^\top x^2$?，并根据梯度下降公式计算对?x?的偏导

\frac{\partial \mathrm{sphere}( x)}{\partial x} = 2 w \odot x

其中$\odot$表示逐元素积。

代码的工程目录如下：

L1.py

引入头文件

from nndl.op import Op
import torch
import copy
import numpy as np
import matplotlib.pyplot as plt

将被优化函数实现为OptimizedFunction算子，其forward方法是Sphere函数的前向计算，backward方法则计算被优化函数对?x?的偏导。代码实现如下：

class OptimizedFunction(Op):
    def __init__(self, w):
        super(OptimizedFunction, self).__init__()
        self.w = torch.as_tensor(w, dtype=torch.float32)
        self.params = {'x': torch.as_tensor(0, dtype=torch.float32)}
        self.grads = {'x': torch.as_tensor(0, dtype=torch.float32)}

    def forward(self, x):
        self.params['x'] = x
        return torch.matmul(self.w.T, torch.square(self.params['x']))

    def backward(self):
        self.grads['x'] = 2 * torch.multiply(self.w.T, self.params['x'])

训练函数?定义一个简易的训练函数，记录梯度下降过程中每轮的参数?x?和损失。代码实现如下：?

def train_f(model, optimizer, x_init, epoch):
    x = x_init
    all_x = []
    losses = []
    for i in range(epoch):
        all_x.append(copy.copy(x.numpy()))
        loss = model(x)
        losses.append(loss)
        model.backward()
        optimizer.step()
        x = model.params['x']
    return torch.as_tensor(np.array(all_x)), losses

可视化函数?定义一个Visualization类，用于绘制?x?的更新轨迹。代码实现如下：

class Visualization(object):
    def __init__(self):
        x1 = np.arange(-5, 5, 0.1)
        x2 = np.arange(-5, 5, 0.1)
        x1, x2 = np.meshgrid(x1, x2)
        self.init_x = torch.as_tensor(np.array([x1, x2]))

    def plot_2d(self, model, x, fig_name):
        fig, ax = plt.subplots(figsize=(10, 6))
        cp = ax.contourf(self.init_x[0], self.init_x[1], model(self.init_x.transpose(1, 0)),
                         colors=['#e4007f', '#f19ec2', '#e86096', '#eb7aaa', '#f6c8dc', '#f5f5f5', '#000000'])
        c = ax.contour(self.init_x[0], self.init_x[1], model(self.init_x.transpose(1, 0)), colors='black')
        cbar = fig.colorbar(cp)
        ax.plot(x[:, 0], x[:, 1], '-o', color='#000000')
        ax.plot(0, 'w*', markersize=18)

        ax.set_xlabel('$x1$')
        ax.set_ylabel('$x2$')

        ax.set_xlim((-2, 5))
        ax.set_ylim((-2, 5))
        # plt.savefig(fig_name)
        plt.show()

定义train_and_plot_f函数，调用train_f和Visualization，训练模型并可视化参数更新轨迹。代码实现如下：

def train_and_plot_f(model, optimizer, epoch, fig_name):
    x_init = torch.as_tensor([3, 4], dtype=torch.float32)
    print('x1 initiate: {}, x2 initiate: {}'.format(x_init[0].numpy(), x_init[1].numpy()))
    x, losses = train_f(model, optimizer, x_init, epoch)
    losses = np.array(losses)

    # 展示x1、x2的更新轨迹
    vis = Visualization()
    vis.plot_2d(model, x, fig_name)

最后一步，模型训练与可视化? 指定Sphere函数中?w?的值，实例化被优化函数，通过小批量梯度下降法更新参数，并可视化?x?的更新轨迹。

from nndl.op import SimpleBatchGD

# 固定随机种子
torch.seed()
w = torch.as_tensor([0.2, 2])
model = OptimizedFunction(w)
opt = SimpleBatchGD(init_lr=0.2, model=model)
train_and_plot_f(model, opt, epoch=20, fig_name='opti-vis-para.pdf')

from nndl.op import Adagrad

# 固定随机种子
torch.seed()
w = torch.as_tensor([0.2, 2])
model2 = OptimizedFunction(w)
opt2 = Adagrad(init_lr=0.5, model=model2, epsilon=1e-7)
train_and_plot_f(model2, opt2, epoch=50, fig_name='opti-vis-para2.pdf')

from nndl.op import RMSprop

# 固定随机种子
torch.seed()
w = torch.as_tensor([0.2, 2])
model3 = OptimizedFunction(w)
opt3 = RMSprop(init_lr=0.1, model=model3, beta=0.9, epsilon=1e-7)
train_and_plot_f(model3, opt3, epoch=50, fig_name='opti-vis-para3.pdf')

from nndl.op import Momentum

# 固定随机种子
torch.seed()
w = torch.as_tensor([0.2, 2])
model4 = OptimizedFunction(w)
opt4 = Momentum(init_lr=0.01, model=model4, rho=0.9)
train_and_plot_f(model4, opt4, epoch=50, fig_name='opti-vis-para4.pdf')

from nndl.op import Adam

# 固定随机种子
torch.seed()
w = torch.as_tensor([0.2, 2])
model5 = OptimizedFunction(w)
opt5 = Adam(init_lr=0.2, model=model5, beta1=0.9, beta2=0.99, epsilon=1e-7)
train_and_plot_f(model5, opt5, epoch=20, fig_name='opti-vis-para5.pdf')

op.py

op文件主要是保存的各个学习器的算子等等，代码如下：

from abc import abstractmethod
import torch


class Op(object):
    def __init__(self):
        pass

    def __call__(self, inputs):
        return self.forward(torch.as_tensor(inputs,dtype=torch.float32))

    def forward(self, inputs):
        raise NotImplementedError

    def backward(self, inputs):
        raise NotImplementedError


# 优化器基类
class Optimizer(object):
    def __init__(self, init_lr, model):
        self.init_lr = init_lr
        #指定优化器需要优化的模型
        self.model = model

    @abstractmethod
    def step(self):
        pass

（1）SimpleBatchGD

????????梯度下降优化器SimpleBatchGD。按照梯度下降的梯度更新公式?$\theta_t \leftarrow \theta_{t-1} - \alpha \mathbf g_t$?进行梯度更新。

class SimpleBatchGD(Optimizer):
    def __init__(self, init_lr, model):
        super(SimpleBatchGD, self).__init__(init_lr=init_lr, model=model)

    def step(self):
        #参数更新
        if isinstance(self.model.params, dict):
            for key in self.model.params.keys():
                self.model.params[key] = self.model.params[key] - self.init_lr * self.model.grads[key]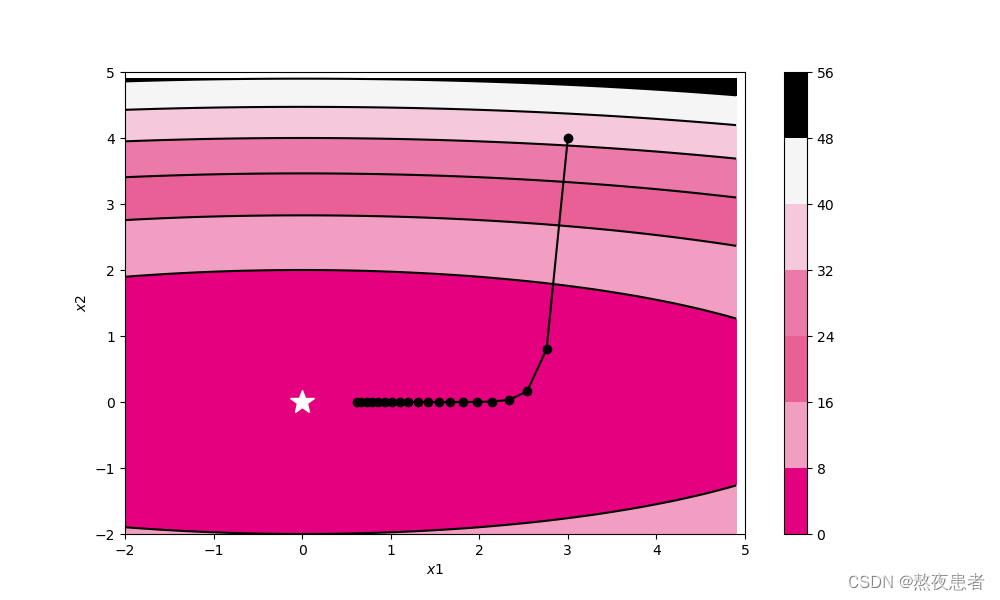

（2）Adagrad

AdaGrad算法（Adaptive Gradient Algorithm，自适应梯度算法)是借鉴 $\ell_2$ 正则化的思想，每次迭代时自适应地调整每个参数的学习率。在第?$t$?次迭代时，先计算每个参数梯度平方的累计值。

G_t = \sum^t_{\tau=1} \mathbf g_{\tau} \odot \mathbf g_{\tau}

其中?$\odot$?为按元素乘积，$\mathbf g_{\tau} \in \mathbb R^{\mid \theta \mid}$?是第?$\tau$?次迭代时的梯，G_t?为梯度平方的累计值

\Delta \theta_t = - \frac{\alpha}{\sqrt{G_t + \epsilon}} \odot \mathbf g_{t}

$\theta_t \leftarrow \theta_{t-1} - \frac{\alpha}{\sqrt{G_t + \epsilon}} \odot \mathbf g_{t} $

其中?$\alpha$?是初始的学习率，?$\epsilon$?是为了保持数值稳定性而设置的非常小的常数，一般取值?e^{-7}?到?e^{-10}?。此外，这里的开平方、除、加运算都是按元素进行的操作。

torch.optim.Adagrad(params, lr=0.01, lr_decay=0, weight_decay=0, initial_accumulator_value=0, eps=1e-10)
  • 如果某个参数的偏导数累积比较大，其学习率相对较小
  • 如果某个参数的偏导数累积比较小，其学习率相对较大

构建优化器? 定义Adagrad类，继承Optimizer类。定义step函数调用adagrad进行参数更新。代码实现如下：

class Adagrad(Optimizer):
    def __init__(self, init_lr, model, epsilon):
        super(Adagrad, self).__init__(init_lr=init_lr, model=model)
        self.G = {}
        for key in self.model.params.keys():
            self.G[key] = 0
        self.epsilon = epsilon

    def adagrad(self, x, gradient_x, G, init_lr):
        G += gradient_x ** 2
        x -= init_lr / torch.sqrt(G + self.epsilon) * gradient_x
        return x, G

    def step(self):
        for key in self.model.params.keys():
            self.model.params[key], self.G[key] = self.adagrad(self.model.params[key],
                                                               self.model.grads[key],
                                                               self.G[key],
                                                               self.init_lr)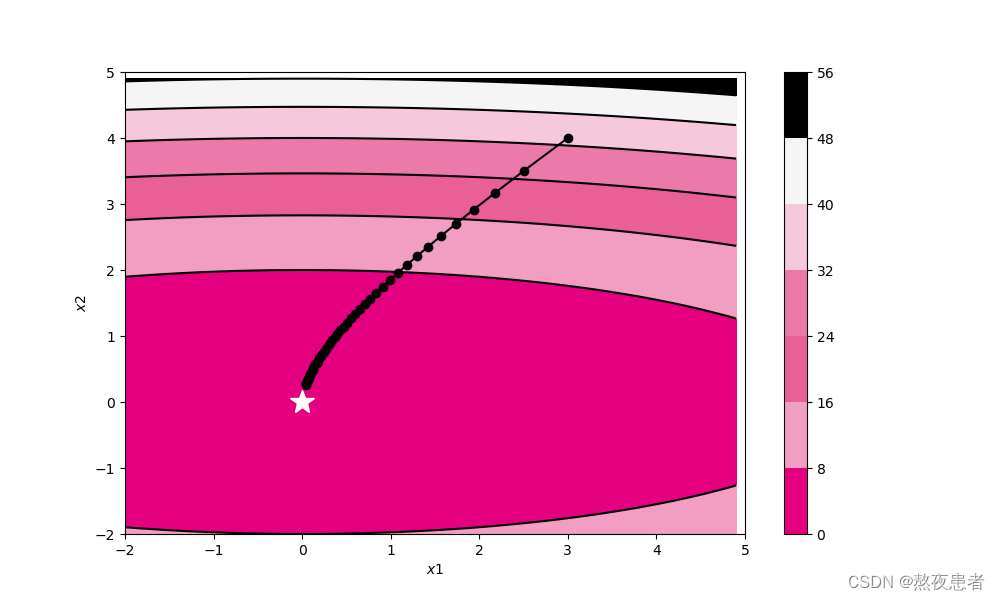

（3）RMSprop

RMSprop算法是一种自适应学习率的方法，可以在有些情况下避免AdaGrad算法中学习率不断单调下降以至于过早衰减的缺点。

RMSprop算法首先计算每次迭代梯度平方?$\mathbf g_{t}^{2}$?的加权移动平均（指数衰减移动平均）

G_t = \beta G_{t-1} + (1 - \beta) \mathbf g_t \odot \mathbf g_t

其中?$\beta$?为衰减率，一般取值为0.9。

RMSprop算法的参数更新差值为：

\Delta \theta_t = - \frac{\alpha}{\sqrt{G_t + \epsilon}} \odot \mathbf g_t

$\theta_t \leftarrow \theta_{t-1} - \frac{\alpha}{\sqrt{G_t + \epsilon}} \odot \mathbf g_{t} $

其中?$\alpha$?是初始的学习率，比如0.001。RMSprop算法和AdaGrad算法的区别在于RMSprop算法中?$G_t$?的计算由累积方式变成了加权移动平均。在迭代过程中，每个参数的学习率并不是呈衰减趋势，既可以变小也可以变大。

torch.optim.RMSprop(params, lr=0.01, alpha=0.99, eps=1e-08, weight_decay=0, momentum=0, centered=False)

构建优化器? 定义RMSprop类，继承Optimizer类。定义step函数调用rmsprop更新参数。代码实现如下：

class RMSprop(Optimizer):
    def __init__(self, init_lr, model, beta, epsilon):
        super(RMSprop, self).__init__(init_lr=init_lr, model=model)
        self.G = {}
        for key in self.model.params.keys():
            self.G[key] = 0
        self.beta = beta
        self.epsilon = epsilon

    def rmsprop(self, x, gradient_x, G, init_lr):
        """
        rmsprop算法更新参数，G为迭代梯度平方的加权移动平均
        """
        G = self.beta * G + (1 - self.beta) * gradient_x ** 2
        x -= init_lr / torch.sqrt(G + self.epsilon) * gradient_x
        return x, G

    def step(self):
        """参数更新"""
        for key in self.model.params.keys():
            self.model.params[key], self.G[key] = self.rmsprop(self.model.params[key],
                                                               self.model.grads[key],
                                                               self.G[key],
                                                               self.init_lr)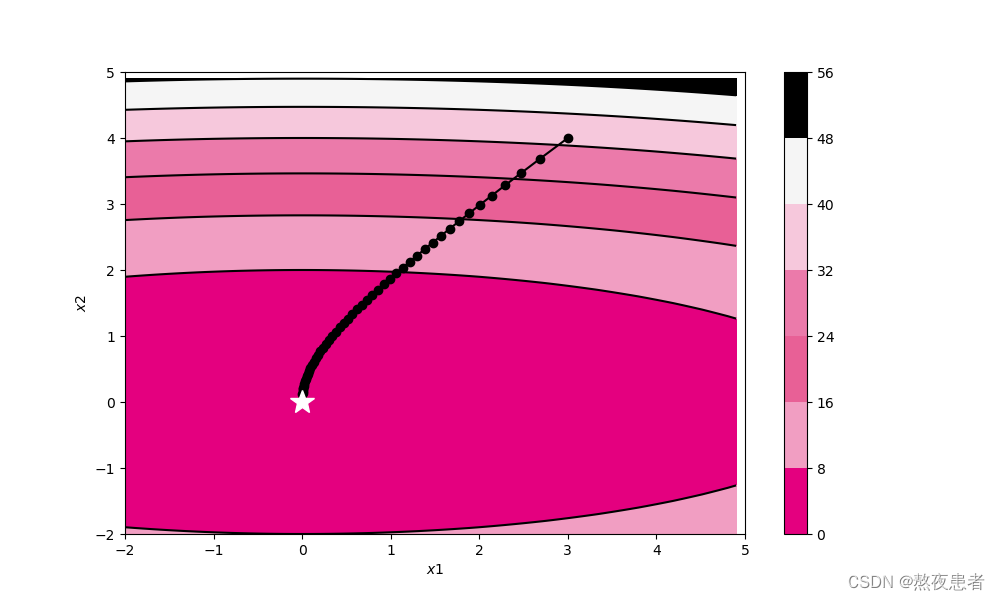

（4）Momentum

动量法（Momentum Method）是用之前积累动量来替代真正的梯度。每次迭代的梯度可以看作加速度。

在第?$t$?次迭代时，计算负梯度的“加权移动平均”作为参数的更新方向，

\Delta \theta_t = \rho \Delta \theta_{t-1} - \alpha \mathbf g_t = - \alpha \sum_{\tau=1}^t\rho^{t - \tau} \mathbf g_{\tau}

其中?$\rho$?为动量因子，通常设为0.9，?$\alpha$?为学习率。

这样，每个参数的实际更新差值取决于最近一段时间内梯度的加权平均值。当某个参数在最近一段时间内的梯度方向不一致时，其真实的参数更新幅度变小。相反，当某个参数在最近一段时间内的梯度方向都一致时，其真实的参数更新幅度变大，起到加速作用。一般而言，在迭代初期，梯度方向都比较一致，动量法会起到加速作用，可以更快地到达最优点。在迭代后期，梯度方向会不一致，在收敛值附近振荡，动量法会起到减速作用，增加稳定性。从某种角度来说，当前梯度叠加上部分的上次梯度，一定程度上可以近似看作二阶梯度。

当然如果就看理论可能不太好理解，看图

这个图其实较为明确的指出了，最后梯度方向是由前一次的梯度方向和这一次的梯度方向共同决定，如果觉得这个图字母太多不爱看，那看如下这个，我认为是我目前看到的最明了的图：

深度学习优化函数详解（4）-- momentum 动量法_深度学习动量法理论详讲-CSDN博客

构建优化器? 定义Momentum类，继承Optimizer类。定义step函数调用momentum进行参数更新。代码实现如下：

class Momentum(Optimizer):
    def __init__(self, init_lr, model, rho):
        super(Momentum, self).__init__(init_lr=init_lr, model=model)
        self.delta_x = {}
        for key in self.model.params.keys():
            self.delta_x[key] = 0
        self.rho = rho

    def momentum(self, x, gradient_x, delta_x, init_lr):
        """
        momentum算法更新参数，delta_x为梯度的加权移动平均
        """
        delta_x = self.rho * delta_x - init_lr * gradient_x
        x += delta_x
        return x, delta_x

    def step(self):
        """参数更新"""
        for key in self.model.params.keys():
            self.model.params[key], self.delta_x[key] = self.momentum(self.model.params[key],
                                                                      self.model.grads[key],
                                                                      self.delta_x[key],
                                                                      self.init_lr)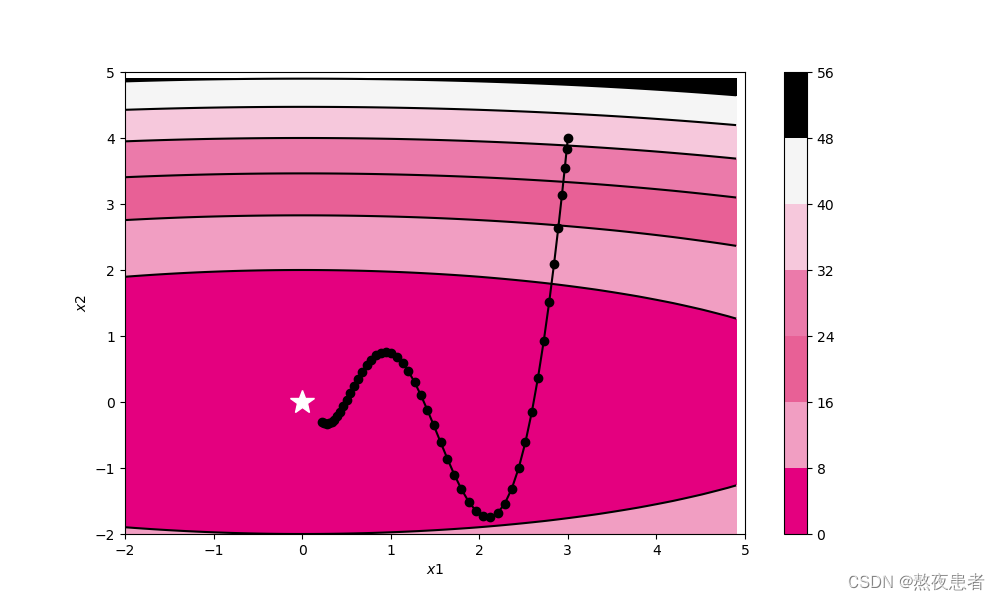

（5）Adam

Adam算法（Adaptive Moment Estimation Algorithm，自适应矩估计算法）可以看作动量法和RMSprop算法的结合，不但使用动量作为参数更新方向，而且可以自适应调整学习率。

Adam算法一方面计算梯度平方?$\mathbf g_t^2$?的加权移动平均（和RMSprop算法类似），另一方面计算梯度?$\mathbf g_t$?的加权移动平均（和动量法类似）。

M_t = \beta_1 M_{t-1} + (1 - \beta_1)\mathbf g_t \\ G_t = \beta_2 G_{t-1} + (1 - \beta_2)\mathbf g_t \odot \mathbf g_t

其中?$\beta_1$?和?$\beta_2$?分别为两个移动平均的衰减率，通常取值为?$\beta_1 = 0.9, \beta_2 = 0.99$?。我们可以把?$M_t$?和?$G_t$?分别看作梯度的均值(一阶矩)和未减去均值的方差(二阶矩)。

假设?$M_0 = 0, G_0 = 0$?，那么在迭代初期?$M_t$?和?$G_t$?的值会比真实的均值和方差要小。特别是当?$\beta_1$?和?$\beta_2$?都接近于1时，偏差会很大。因此，需要对偏差进行修正。

\hat M_t = \frac{M_t}{1 - \beta^t_1} \\ \hat G_t = \frac{G_t}{1 - \beta^t_2}

Adam算法的参数更新差值为

\Delta \theta_t = - \frac{\alpha}{\sqrt{\hat G_t + \epsilon}}\hat M_t

其中学习率?$\alpha$?通常设为0.001，并且也可以进行衰减，比如?$a_t = \frac{a_0}{\sqrt{t}}$?。

构建优化器? 定义Adam类，继承Optimizer类。定义step函数调用adam函数更新参数。代码实现如下：

class Adam(Optimizer):
    def __init__(self, init_lr, model, beta1, beta2, epsilon):
        super(Adam, self).__init__(init_lr=init_lr, model=model)
        self.beta1 = beta1
        self.beta2 = beta2
        self.epsilon = epsilon
        self.M, self.G = {}, {}
        for key in self.model.params.keys():
            self.M[key] = 0
            self.G[key] = 0
        self.t = 1

    def adam(self, x, gradient_x, G, M, t, init_lr):
        M = self.beta1 * M + (1 - self.beta1) * gradient_x
        G = self.beta2 * G + (1 - self.beta2) * gradient_x ** 2
        M_hat = M / (1 - self.beta1 ** t)
        G_hat = G / (1 - self.beta2 ** t)
        t += 1
        x -= init_lr / torch.sqrt(G_hat + self.epsilon) * M_hat
        return x, G, M, t

    def step(self):
        """参数更新"""
        for key in self.model.params.keys():
            self.model.params[key], self.G[key], self.M[key], self.t = self.adam(self.model.params[key],
                                                                                 self.model.grads[key],
                                                                                 self.G[key],
                                                                                 self.M[key],
                                                                                 self.t,
                                                                                 self.init_lr)

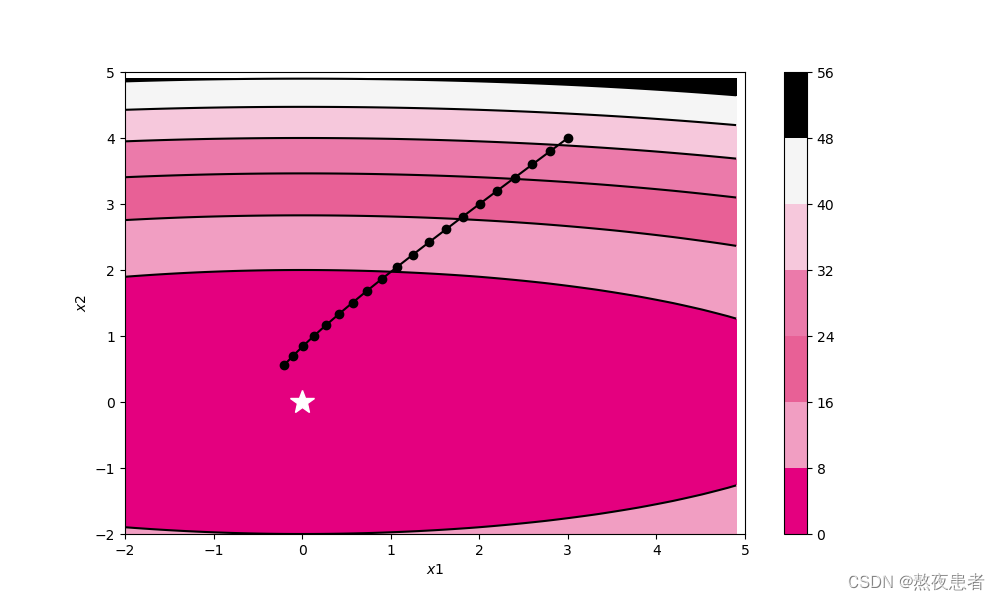
2.被优化函数?x^{2}/20+y^{2}?

预期结果如下:

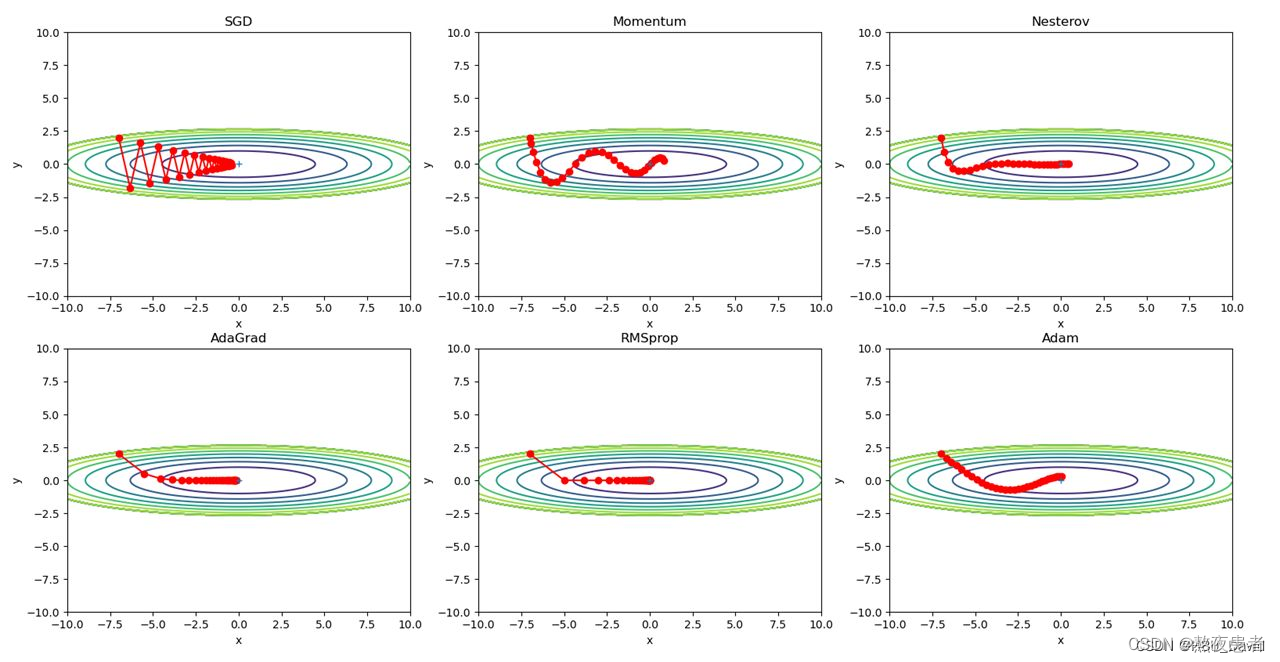
代码如下,来源老师的博客【NNDL 作业】优化算法比较 增加 RMSprop、Nesterov_随着优化的进展,需要调整γ吗?rmsprop算法习题-CSDN博客

# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict


class SGD:
    """随机梯度下降法（Stochastic Gradient Descent）"""

    def __init__(self, lr=0.01):
        self.lr = lr

    def update(self, params, grads):
        for key in params.keys():
            params[key] -= self.lr * grads[key]


class Momentum:
    """Momentum SGD"""

    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None

    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)

        for key in params.keys():
            self.v[key] = self.momentum * self.v[key] - self.lr * grads[key]
            params[key] += self.v[key]


class Nesterov:
    """Nesterov's Accelerated Gradient (http://arxiv.org/abs/1212.0901)"""

    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None

    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)

        for key in params.keys():
            self.v[key] *= self.momentum
            self.v[key] -= self.lr * grads[key]
            params[key] += self.momentum * self.momentum * self.v[key]
            params[key] -= (1 + self.momentum) * self.lr * grads[key]


class AdaGrad:
    """AdaGrad"""

    def __init__(self, lr=0.01):
        self.lr = lr
        self.h = None

    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)

        for key in params.keys():
            self.h[key] += grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)


class RMSprop:
    """RMSprop"""

    def __init__(self, lr=0.01, decay_rate=0.99):
        self.lr = lr
        self.decay_rate = decay_rate
        self.h = None

    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)

        for key in params.keys():
            self.h[key] *= self.decay_rate
            self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)


class Adam:
    """Adam (http://arxiv.org/abs/1412.6980v8)"""

    def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
        self.lr = lr
        self.beta1 = beta1
        self.beta2 = beta2
        self.iter = 0
        self.m = None
        self.v = None

    def update(self, params, grads):
        if self.m is None:
            self.m, self.v = {}, {}
            for key, val in params.items():
                self.m[key] = np.zeros_like(val)
                self.v[key] = np.zeros_like(val)

        self.iter += 1
        lr_t = self.lr * np.sqrt(1.0 - self.beta2 ** self.iter) / (1.0 - self.beta1 ** self.iter)

        for key in params.keys():
            self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
            self.v[key] += (1 - self.beta2) * (grads[key] ** 2 - self.v[key])

            params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)


def f(x, y):
    return x ** 2 / 20.0 + y ** 2


def df(x, y):
    return x / 10.0, 2.0 * y


init_pos = (-7.0, 2.0)
params = {}
params['x'], params['y'] = init_pos[0], init_pos[1]
grads = {}
grads['x'], grads['y'] = 0, 0

learningrate = [0.9, 0.3, 0.3, 0.6, 0.6, 0.6, 0.6]
optimizers = OrderedDict()
optimizers["SGD"] = SGD(lr=learningrate[0])
optimizers["Momentum"] = Momentum(lr=learningrate[1])
optimizers["Nesterov"] = Nesterov(lr=learningrate[2])
optimizers["AdaGrad"] = AdaGrad(lr=learningrate[3])
optimizers["RMSprop"] = RMSprop(lr=learningrate[4])
optimizers["Adam"] = Adam(lr=learningrate[5])

idx = 1
id_lr = 0

for key in optimizers:
    optimizer = optimizers[key]
    lr = learningrate[id_lr]
    id_lr = id_lr + 1
    x_history = []
    y_history = []
    params['x'], params['y'] = init_pos[0], init_pos[1]

    for i in range(30):
        x_history.append(params['x'])
        y_history.append(params['y'])

        grads['x'], grads['y'] = df(params['x'], params['y'])
        optimizer.update(params, grads)

    x = np.arange(-10, 10, 0.01)
    y = np.arange(-5, 5, 0.01)

    X, Y = np.meshgrid(x, y)
    Z = f(X, Y)
    # for simple contour line
    mask = Z > 7
    Z[mask] = 0

    # plot
    plt.subplot(2, 3, idx)
    idx += 1
    plt.plot(x_history, y_history, 'o-', color="r")
    # plt.contour(X, Y, Z)  # 绘制等高线
    plt.contour(X, Y, Z, cmap='gray')  # 颜色填充
    plt.ylim(-10, 10)
    plt.xlim(-10, 10)
    plt.plot(0, 0, '+')
    # plt.axis('off')
    # plt.title(key+'\nlr='+str(lr), fontstyle='italic')
    plt.text(0, 10, key + '\nlr=' + str(lr), fontsize=20, color="b",
             verticalalignment='top', horizontalalignment='center', fontstyle='italic')
    plt.xlabel("x")
    plt.ylabel("y")

plt.subplots_adjust(wspace=0, hspace=0)  # 调整子图间距
plt.show()

结果如下：

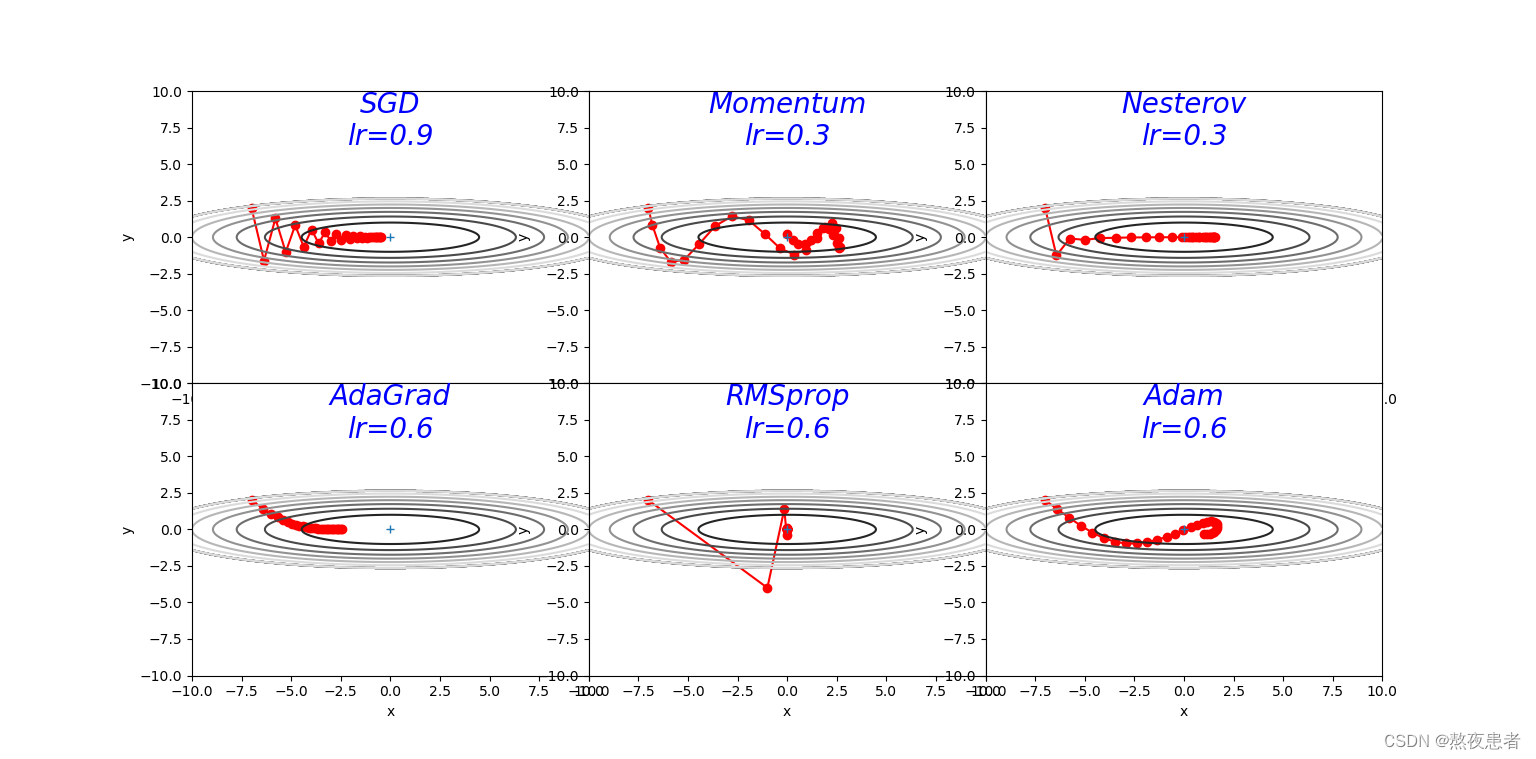
?3.解释不同轨迹的形成原因，并分析各个算法的优缺点

（1）SimpleBatchGD

轨迹形成原因：SGD收敛轨迹呈“之”字形的原因主要是由于梯度下降过程中，学习率过高或者数据集中存在一些特殊情况（如个别样本的梯度值与其他样本相比过大或过小），导致更新方向在每次迭代中变化很大，使得算法无法稳定地朝着全局最优解的方向前进。如果在函数的形状非均向时，单纯朝着梯度方向更新参数，容易使得算法在某些方向上的更新幅度大，而在其他方向上的更新幅度小，从而出现“之”字形的收敛轨迹。

优点：

????????由于不是在全部训练数据上的损失函数，而是在每轮迭代中，随机优化某一条训练数据上的损失函数，这样每一轮参数的更新速度大大加快。
缺点：

  1. 准确度下降。由于即使在目标函数为强凸函数的情况下，SGD仍旧无法做到线性收敛。
  2. 可能会收敛到局部最优，由于单个样本并不能代表全体样本的趋势.
  3. 不易于并行实现。

（2）Adagrad

轨迹形成的原因:函数的取值高效地向着最小值移动。 由于y轴方向上的梯度较大，因此刚开始变动较大，但是后面会根据这个较大的变动按比例进行调整，减小更新的步伐。 因此y轴方向上的更新程度被减弱，“之”字形的变动程度有所衰减.

优点：

  1. 自适应学习率：AdaGrad算法通过自适应地调整学习率，能够更好地适应不同的参数更新情况，提高了算法的效率和稳定性。

  2. 支持稀疏数据：AdaGrad算法能够自适应地调整每个参数的学习率，对于稀疏数据能够更好地适应和处理。

  3. 不需要手动调整学习率：AdaGrad算法不需要手动调整学习率，能够减少调参的时间和成本。

缺点：

  1. 无法处理非凸函数：由于学习率的不断衰减，AdaGrad算法可能会在后期陷入局部最优解，无法处理非凸函数。

  2. 参数更新过于激进：由于学习率的不断减小，AdaGrad算法可能会导致部分参数更新过于激进，导致优化过程不稳定。

  3. 可能会出现过拟合：由于学习率的逐渐减小，AdaGrad算法可能会导致过早停止更新，出现过拟合的情况。

（3）RMSprop

轨迹形成原因：RMSprop算法相较于AdaGrad算法，在学习率变化方面表现更加平缓和稳定，因此能够更有效地收敛到损失函数的最小值。它通过引入指数加权移动平均来调整学习率，使得在训练过程中逐渐遗忘过去的梯度，只受近期梯度的影响。这样可以解决AdaGrad算法在训练后期学习率衰减过快的问题。

优点：

  1. 自适应学习率：RMSprop算法通过自适应地调整学习率和梯度的平均值，能够更好地适应不同的参数更新情况，提高了算法的效率和稳定性。

  2. 支持稀疏数据：RMSprop算法能够自适应地调整每个参数的学习率和梯度平均值，对于稀疏数据能够更好地适应和处理。

  3. 收敛速度快：由于学习率和梯度平均值的自适应调整，RMSprop算法在优化过程中能够更快地收敛到最优解。

缺点：

  1. 对超参数敏感：RMSprop算法对超参数的选择非常敏感，可能需要进行比较多的调参才能得到最优的结果。

  2. 可能会出现震荡：由于学习率和梯度平均值的自适应调整，RMSprop算法可能会导致参数更新方向的变化，出现震荡的情况。

  3. 可能会导致梯度消失或爆炸：由于梯度平均值的存在，RMSprop算法可能会导致梯度消失或爆炸的问题。

（4）Momentum

轨迹形成的原因:x轴方向上受到的力小，一直在同向受力，所以会加速。y轴方向上受到的力大，交互正反向的力，会互相抵消。和SGD相比，可更快朝x轴方向靠近，减弱“之”字形变动程度.

优点：

  1. 加速收敛：Momentum算法可以加速模型训练的收敛速度，特别是在出现局部最小值或平坦区域时，能够帮助模型跳出局部最小值并快速朝向全局最优解。

  2. 抑制震荡：由于动量的引入，Momentum算法有助于抑制参数更新过程中的震荡，使得模型训练更加稳定。

  3. 减少方向变化：在参数更新时，Momentum算法可以减少因梯度方向变化导致的参数更新幅度剧烈波动，从而使得参数更新更加平滑。

缺点：

  1. 需要调节超参数：Momentum算法需要调节一个称为动量系数的超参数，选择不合适的动量系数可能导致模型表现不佳。

  2. 可能陷入局部最小值：由于动量的引入，Momentum算法在一些情况下可能无法精确地收敛到全局最小值，而是停留在局部最小值附近。

  3. 对某些数据集不适用：Momentum算法在某些数据集上可能表现不佳，特别是在具有大量平坦区域的数据集上，可能导致算法在平坦区域震荡并难以收敛。

（5）Adam

轨迹形成原因：Adam算法结合了动量法和RMSprop算法的优点，可以自适应地调整学习率，并且在训练过程中能够快速收敛到最优点。由于Adam算法同时考虑了梯度的一阶矩估计（类似于动量）和二阶矩估计（类似于RMSprop），因此在参数更新过程中更加平稳和稳定。使其收敛轨迹图通常表现为前期收敛幅度较大，后期逐渐平稳，朝着最优点不断移动的特点。

优点：

  1. 自适应调节：Adam算法可以自适应地调节每个参数的学习率，根据每个参数的历史梯度信息和动量来计算每个参数的有效学习率，从而使得参数更新更加准确和高效。

  2. 加速收敛：Adam算法通过自适应调节学习率，可以加速模型训练的收敛速度，在相同迭代次数下比Momentum和Adagrad算法更快地收敛。

  3. 适用于大规模数据集：Adam算法对于大规模数据集和高维度数据具有很好的表现，可以在保证效果的同时，减少了调参的工作量。

缺点：

  1. 内存占用较高：Adam算法需要保存每个参数的历史梯度信息和动量，因此内存占用较高，尤其是对于大规模模型和大规模数据集，可能会导致内存不足的问题。

  2. 对超参数敏感：Adam算法需要调节一些超参数，如学习率、动量系数以及两个平滑系数，选择不合适的超参数可能导致模型性能下降。

  3. 可能出现过拟合：由于Adam算法中引入了动量和自适应调节学习率的机制，可能导致在某些情况下发生过拟合现象。

总结

本次实验难度较小，代码只需要跑一遍即可，真正难得是把这几个优化算法彻底搞明白，搞彻底，我大概做了一个思维导图，简单对优化算法进行了总结。

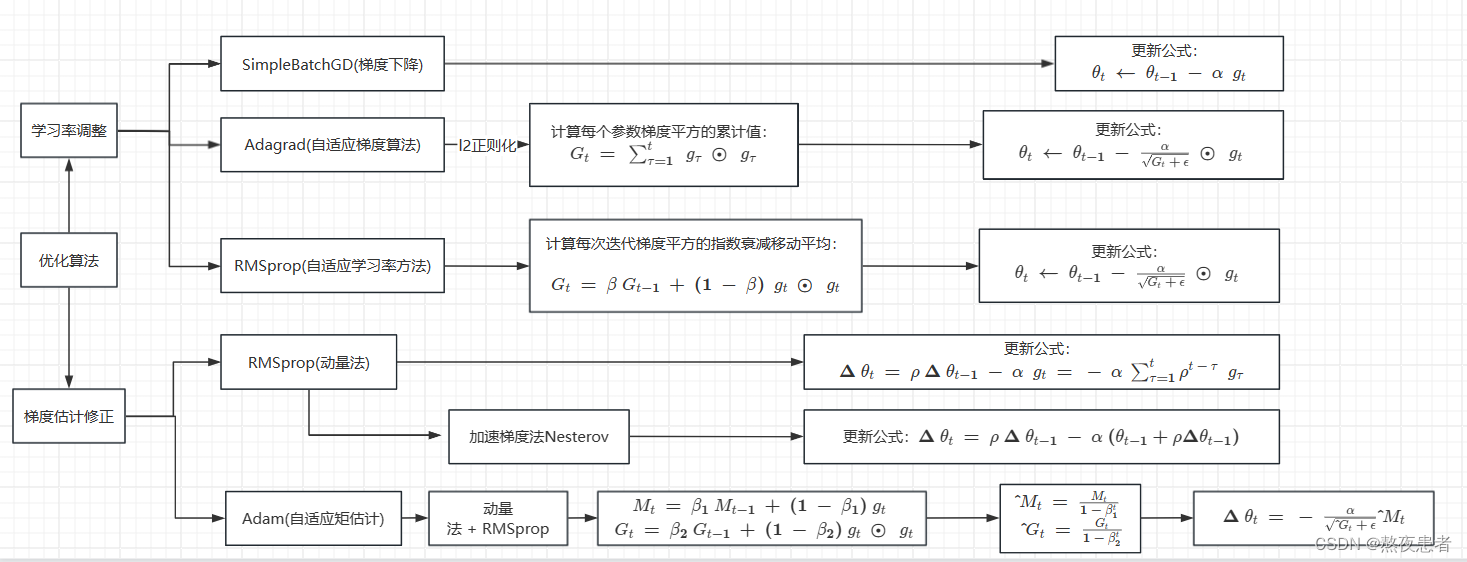
DL-优化算法| ProcessOn免费在线作图,在线流程图,在线思维导图

参考文献

RMSprop — PyTorch 2.1 documentation

深度学习优化函数详解（4）-- momentum 动量法_深度学习动量法理论详讲-CSDN博客

RMSprop算法优缺点 - CSDN文库

AdaGrad算法优缺点 - CSDN文库

梯度下降：BGD、SGD、mini-batch GD介绍及其优缺点_sgd和minibatch-CSDN博客

文章来源:https://blog.csdn.net/m0_70026215/article/details/135190183
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。