6.19二叉搜索树中的众数(LC501-E)

算法：

提到二叉搜索树，一定是中序遍历！

双指针法：

pre指向当前节点cur的前一个节点，如果cur.val= pre.val，count++，count用来统计该数值出现的频率

如果 频率count 等于 maxCount（最大频率），当然要把这个元素加入到结果集中。

万一，这个maxCount此时还不是真正最大频率呢。

频率count 大于 maxCount的时候，不仅要更新maxCount，而且要清空结果集（以下代码为result数组），因为结果集之前的元素都失效了。

调试过程：

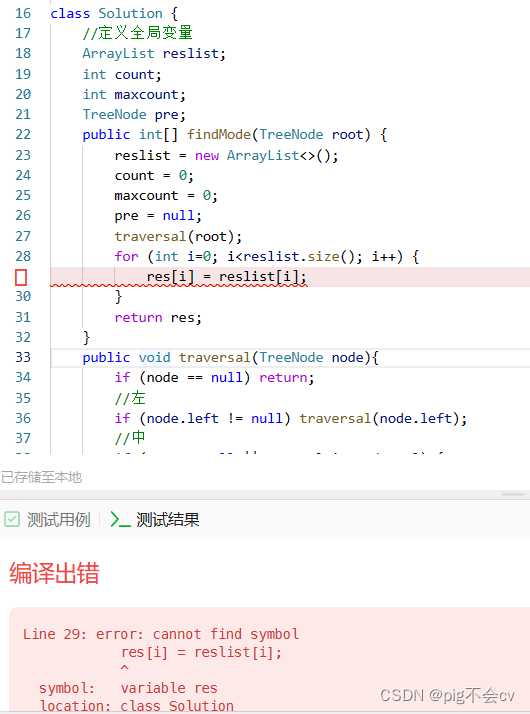
原因：

在Java中，`resList[i]`?是不合法的语法，因为`ArrayList`并不支持通过索引直接访问元素。相反，它使用?`get`?方法来获取特定索引处的元素，因此正确的语法是?`resList.get(i)`。

数组（Array）支持通过索引直接访问元素，因此可以使用?`res[i]`?来访问数组中的元素。但是对于列表（ArrayList）来说，需要使用?`get`?方法来访问特定索引处的元素。

因此，正确的写法是?`res[i] = resList.get(i);

而且，res没有初始化、定义

修改后：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    //定义全局变量
    ArrayList reslist;
    int count;
    int maxcount;
    TreeNode pre;
    public int[] findMode(TreeNode root) {
        reslist = new ArrayList<>();
        count = 0;
        maxcount = 0;
        pre = null;
        int[] res = new int[reslist.size()];
        traversal(root);
        for (int i=0; i<reslist.size(); i++) {
            res[i] = reslist.get(i);
        }
        return res;
    }
    public void traversal(TreeNode node){
        if (node == null) return;
        //左
        if (node.left != null) traversal(node.left);
        //中
        if (pre == null || pre.val != node.val) {
            count = 1;
        }
        else {
            count++;
        }
        if (count > maxcount) {
            reslist.clear();
            maxcount = count;
            reslist.add(node.val);
        }
        else if (count == maxcount) {
            reslist.add(node.val);
        }
        pre = node;
        //右
        if (node.right != null) traversal(node.right);
    }
}

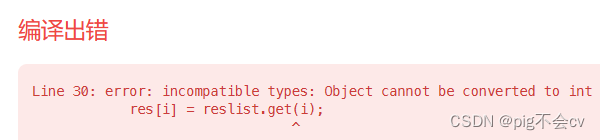
原因：

问题出在?`ArrayList reslist`?的定义上。在 Java 中，如果你没有指定泛型类型，`ArrayList`?默认会将其元素视为?`Object`?类型。因此，在?`int[] res = new int[reslist.size()];`?这一行中，你创建了一个大小为 0 的 int 数组，因为此时?`reslist`?中还没有添加任何元素。

为了解决这个问题，你应该明确定义?`ArrayList`?的元素类型为?`Integer`，而不是使用默认的?`Object`。

修改后:

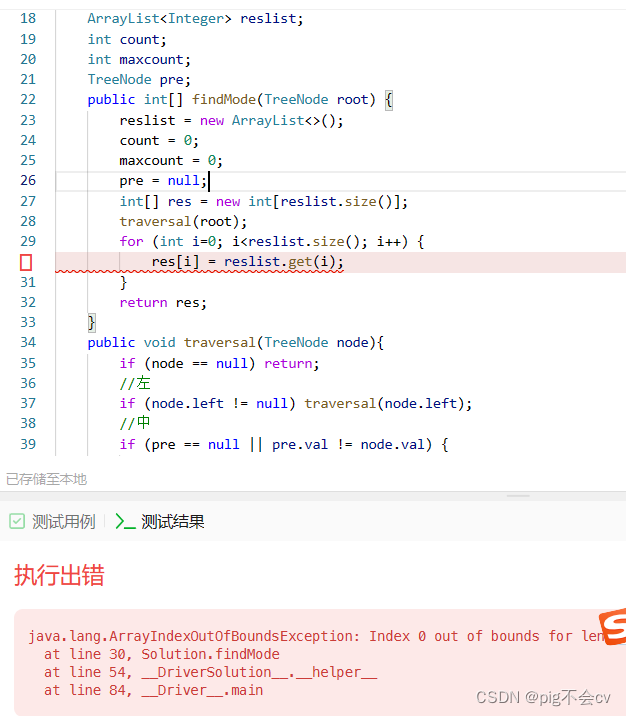
原因：

问题出在创建结果数组?`res`?的时候。在?`int[] res = new int[reslist.size()];`?这一行代码之后立即调用了?`traversal(root);`，这会导致?`res`?数组的大小仍然为0，因为此时?`reslist`?中还没有添加任何元素。

为了解决这个问题，应该将?`int[] res = new int[reslist.size()];`?放在?`traversal(root);`?之后。这样，当?`traversal`?方法执行完毕后，`reslist`?中会包含所有的结果，然后你才能创建相应大小的?`res`?数组，并将结果放入其中。

正确代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    //定义全局变量
    ArrayList<Integer> reslist;
    int count;
    int maxcount;
    TreeNode pre;
    public int[] findMode(TreeNode root) {
        reslist = new ArrayList<>();
        count = 0;
        maxcount = 0;
        pre = null;
        
        traversal(root);
        int[] res = new int[reslist.size()];
        for (int i=0; i<reslist.size(); i++) {
            res[i] = reslist.get(i);
        }
        return res;
    }
    public void traversal(TreeNode node){
        if (node == null) return;
        //左
        if (node.left != null) traversal(node.left);
        //中
        if (pre == null || pre.val != node.val) {
            count = 1;
        }
        else {
            count++;
        }
        if (count > maxcount) {
            reslist.clear();
            maxcount = count;
            reslist.add(node.val);
        }
        else if (count == maxcount) {
            reslist.add(node.val);
        }
        pre = node;
        //右
        if (node.right != null) traversal(node.right);
    }
}

注意：

结果集是ArrayList，要转变成数组。（题目里面的输出结果是数组）

原始的?`reslist`?是一个 ArrayList，它可以动态增长，但在返回结果时，通常更方便将其转换为固定大小的数组。这样做可以更好地符合函数的返回类型，并且更方便在其他地方使用结果。

时间空间复杂度

时间复杂度分析

• 在遍历二叉树的过程中，对于每个节点，我们执行了常数次操作（比较、更新计数器、添加到结果列表等）。
• 假设树中有 (n) 个节点，则时间复杂度为 (O(n))，因为我们对每个节点只进行了常数次操作。

空间复杂度分析

• 空间复杂度取决于递归调用的深度，即树的高度。在最坏的情况下，如果树是一个链状结构，递归调用的深度将是 (O(n))。
• 此外，我们使用了一个 ArrayList 来存储结果，其空间占用与树中节点个数相关，因此空间复杂度也是 (O(n))。

算法的时间复杂度为 (O(n))，空间复杂度也是 (O(n))。