Channel Coding Theorem 证明
防盗 https://www.cnblogs.com/setdong/p/17948414
对应于教材 Elements of Information Theory 的 8.7 章节.
在证明定理之前, 先复习一些背景知识, 包括 entropy, WLLN, AEP, joint AEP 和 DMC. 第二节为定理的声明和证明.
1. background
1.1 Entropies 熵
来自于书中的第二章
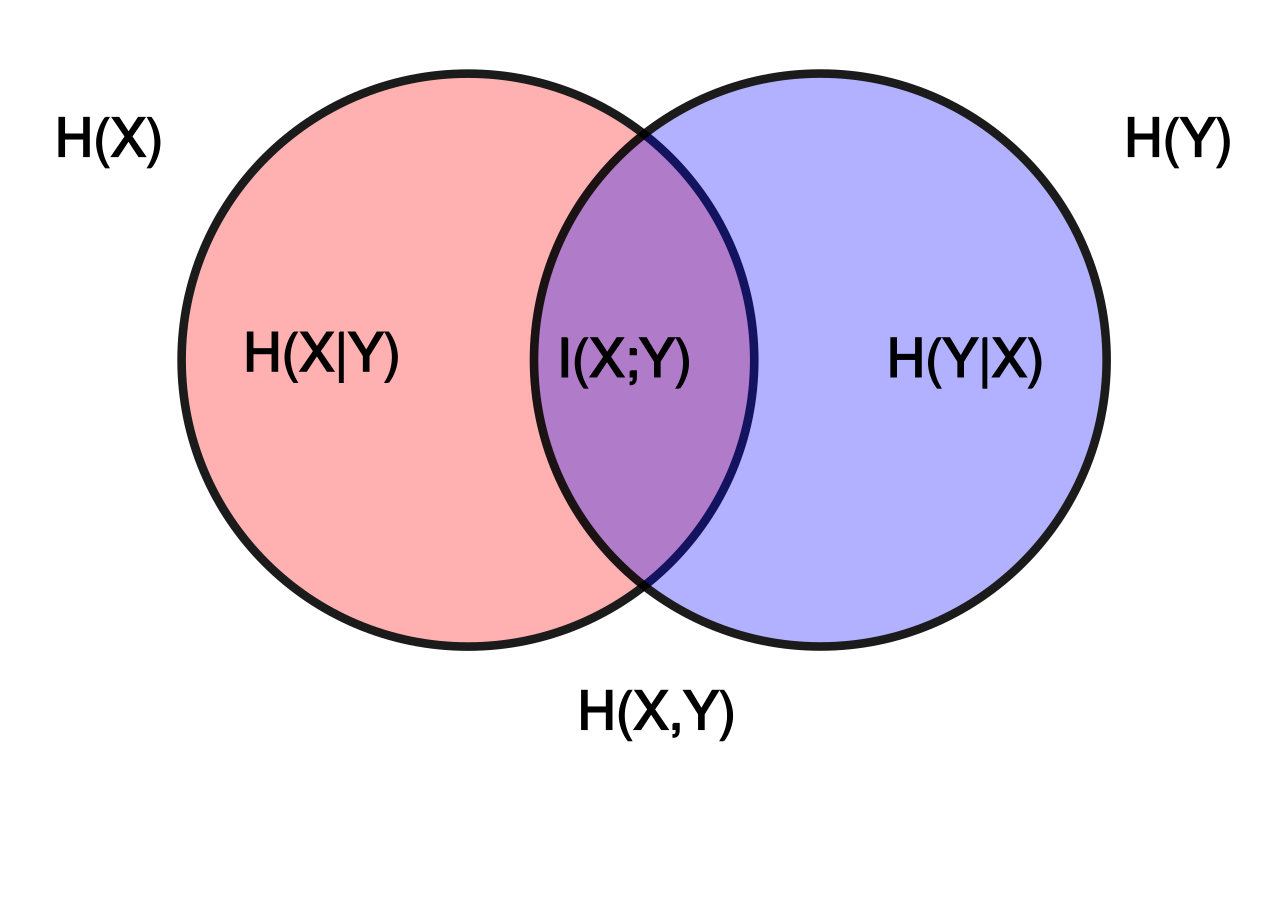
Entropy:
H
(
X
)
=
?
∑
x
∈
S
X
p
(
x
)
log
?
p
(
x
)
=
?
E
[
log
?
p
(
x
)
]
H(X)=-\sum_{x\in S_X} p(x)\log p(x)=-\mathbb{E}[\log p(x)]
H(X)=?x∈SX?∑?p(x)logp(x)=?E[logp(x)]
衡量了一个随机变量的不确定程度/随机性 (uncertainty/ randomness)
Joint entropy 联合熵:
H
(
X
,
Y
)
=
?
∑
x
∈
S
X
∑
y
∈
S
Y
p
(
x
,
y
)
log
?
p
(
x
,
y
)
H(X,Y)=-\sum_{x\in S_X}\sum_{y\in S_Y} p(x,y)\log p(x,y)
H(X,Y)=?x∈SX?∑?y∈SY?∑?p(x,y)logp(x,y)
同样地,
H
(
X
,
Y
)
H(X,Y)
H(X,Y) 衡量的是
X
X
X 和
Y
Y
Y 联合的随机性.
Conditional entropy 条件熵:
H
(
Y
∣
X
)
=
∑
x
∈
S
X
p
(
x
)
H
(
Y
∣
X
=
x
)
H(Y|X)=\sum_{x\in S_X} p(x) H(Y|X=x)
H(Y∣X)=x∈SX?∑?p(x)H(Y∣X=x)
H
(
Y
∣
X
)
H(Y|X)
H(Y∣X) 衡量的是给定
X
X
X 后,
Y
Y
Y 的随机性.
Mutual information 互信息:
I
(
X
;
Y
)
=
H
(
X
)
?
H
(
X
∣
Y
)
I(X;Y)=H(X)-H(X|Y)
I(X;Y)=H(X)?H(X∣Y)
是
X
X
X 由于已知
Y
Y
Y 而减少的“信息量”
1.2 Weak Law of Large Number(WLLN)
X 1 , . . . , X n X_1,...,X_n X1?,...,Xn? are i.i.d ~ p ( x ) \sim p(x) ~p(x), then
1
n
∑
i
=
1
n
X
i
→
in?Prob.
n
→
∞
E
[
X
]
\frac{1}{n}\sum_{i=1}^n X_i \xrightarrow[\text{in Prob.}]{n\rightarrow \infty} \mathbb{E}[X]
n1?i=1∑n?Xi?n→∞in?Prob.?E[X]
即样本均值依概率收敛于期望值.
1.3 AEP: Asymptotic Equipartition Property
来自于书中的第3章
Thm. (AEP) If
X
1
,
.
.
.
,
X
n
X_1,...,X_n
X1?,...,Xn? are i.i.d
~
p
(
x
)
\sim p(x)
~p(x), then
?
1
n
log
?
p
(
X
1
,
.
.
.
,
X
n
)
→
in?Prob.
n
→
∞
H
(
X
)
p
(
X
1
,
.
.
.
,
X
n
)
→
in?Prob.
n
→
∞
2
?
n
H
(
X
)
-\frac{1}{n} \log p(X_1,...,X_n)\xrightarrow[\text{in Prob.}]{n\rightarrow \infty} H(X) \\ p(X_1,...,X_n) \xrightarrow[\text{in Prob.}]{n\rightarrow \infty} 2^{-nH(X)}
?n1?logp(X1?,...,Xn?)n→∞in?Prob.?H(X)p(X1?,...,Xn?)n→∞in?Prob.?2?nH(X)
Typical set (典型集) 定义:
The typical set
A
?
(
n
)
A_{\epsilon}^{(n)}
A?(n)? with respect to
p
(
x
)
p(x)
p(x) is the set of sequences
(
x
1
,
.
.
.
,
x
n
)
∈
S
X
(
n
)
(x_1,...,x_n)\in S_X^{(n)}
(x1?,...,xn?)∈SX(n)? with the property
2
?
n
(
H
(
X
)
+
?
)
≤
p
(
x
1
,
.
.
.
,
x
n
)
≤
2
?
n
(
H
(
X
)
?
?
)
2^{-n(H(X)+\epsilon)}\leq p(x_1,...,x_n)\leq 2^{-n(H(X)-\epsilon)}
2?n(H(X)+?)≤p(x1?,...,xn?)≤2?n(H(X)??)
Typical set 有以下性质:
- If ( x 1 , . . . , x n ) ∈ A ? ( n ) (x_1,...,x_n)\in A_{\epsilon}^{(n)} (x1?,...,xn?)∈A?(n)?, then H ( X ) ? ? ≤ ? 1 n p ( x 1 , . . . , x n ) ≤ H ( X ) + ? H(X) - \epsilon\leq -\frac{1}{n} p(x_1,...,x_n)\leq H(X)+\epsilon H(X)??≤?n1?p(x1?,...,xn?)≤H(X)+?.
- Pr ? { A ? ( n ) } > 1 ? ? \Pr\{A_{\epsilon}^{(n)}\}>1-\epsilon Pr{A?(n)?}>1?? for n n n sufficiently large.
- ∣ A ? ( n ) ∣ ≤ 2 n ( H ( X ) + ? ) |A_{\epsilon}^{(n)}|\leq 2^{n(H(X)+\epsilon)} ∣A?(n)?∣≤2n(H(X)+?).
- ∣ A ? ( n ) ∣ ≥ ( 1 ? ? ) 2 n ( H ( X ) ? ? ) |A_{\epsilon}^{(n)}|\geq (1-\epsilon)2^{n(H(X)-\epsilon)} ∣A?(n)?∣≥(1??)2n(H(X)??) for n n n sufficiently large.
1.4 Joint AEP
来自于书中的8.6章节
Joint typical set 定义:
The set
A
?
(
n
)
A_{\epsilon}^{(n)}
A?(n)? of jointly typical sequences
{
(
x
n
,
y
n
)
}
\{(x^n,y^n)\}
{(xn,yn)} with respect to
p
(
x
,
y
)
p(x,y)
p(x,y) is the set of
n
n
n-sequences with empirical entropies
?
\epsilon
?-close to the true entropies:
A
?
(
n
)
=
{
(
x
n
,
y
n
)
∈
S
X
n
×
S
Y
n
:
∣
?
1
n
log
?
p
(
x
n
)
?
H
(
X
)
∣
<
?
,
∣
?
1
n
log
?
p
(
y
n
)
?
H
(
Y
)
∣
<
?
,
∣
?
1
n
log
?
p
(
x
n
,
y
n
)
?
H
(
X
,
Y
)
∣
<
?
}
A_{\epsilon}^ {(n)}=\{(x^n,y^n)\in S_X^n \times S_Y^n:\\ |-\frac{1}{n}\log p(x^n)-H(X)|<\epsilon,\\ |-\frac{1}{n}\log p(y^n)-H(Y)|<\epsilon,\\ |-\frac{1}{n}\log p(x^n,y^n)-H(X,Y)|<\epsilon\}
A?(n)?={(xn,yn)∈SXn?×SYn?:∣?n1?logp(xn)?H(X)∣<?,∣?n1?logp(yn)?H(Y)∣<?,∣?n1?logp(xn,yn)?H(X,Y)∣<?}
where
p
(
x
n
,
y
n
)
=
∏
i
=
1
n
p
(
x
i
,
y
i
)
p(x^n,y^n)=\prod_{i=1}^{n} p(x_i,y_i)
p(xn,yn)=∏i=1n?p(xi?,yi?).
Thm.(Joint AEP) Let
(
X
n
,
Y
n
)
(X^n, Y^n)
(Xn,Yn) be sequences of length
n
n
n drawn i.i.d.
~
p
(
x
n
,
y
n
)
=
∏
i
=
1
n
p
(
x
i
,
y
i
)
\sim p(x^n,y^n)=\prod_{i=1}^n p(x_i,y_i)
~p(xn,yn)=∏i=1n?p(xi?,yi?). Then,
- As n → ∞ n\rightarrow \infty n→∞, Pr ? { ( X n , Y n ) ∈ A ? ( n ) } → 1 \Pr \{(X^n, Y^n)\in A_\epsilon^{(n)}\}\rightarrow 1 Pr{(Xn,Yn)∈A?(n)?}→1
-
∣
A
?
(
n
)
∣
≤
2
n
(
H
(
X
,
Y
)
+
?
)
|A_\epsilon^{(n)}|\leq 2^{n(H(X,Y)+\epsilon)}
∣A?(n)?∣≤2n(H(X,Y)+?)
∣ A ? ( n ) ∣ ≥ ( 1 ? ? ) 2 n ( H ( X , Y ) ? ? ) |A_\epsilon^{(n)}|\geq (1-\epsilon)2^{n(H(X,Y)-\epsilon)} ∣A?(n)?∣≥(1??)2n(H(X,Y)??) for sufficiently large n n n - If
(
X
~
n
,
Y
~
n
)
~
p
(
x
n
)
p
(
y
n
)
(\tilde{X}^n, \tilde{Y}^n)\sim p(x^n)p(y^n)
(X~n,Y~n)~p(xn)p(yn), then
Pr ? { ( X ~ n , Y ~ n ) ∈ A ? ( n ) } ≤ 2 ? n ( I ( X ; Y ) ? 3 ? ) \Pr \{(\tilde{X}^n, \tilde{Y}^n)\in A_\epsilon^{(n)}\}\leq 2^{-n(I(X;Y)-3\epsilon)} Pr{(X~n,Y~n)∈A?(n)?}≤2?n(I(X;Y)?3?)
Pr ? { ( X ~ n , Y ~ n ) ∈ A ? ( n ) } ≤ ( 1 ? ? ) 2 ? n ( I ( X ; Y ) + 3 ? ) \Pr \{(\tilde{X}^n, \tilde{Y}^n)\in A_\epsilon^{(n)}\}\leq (1-\epsilon)2^{-n(I(X;Y)+3\epsilon)} Pr{(X~n,Y~n)∈A?(n)?}≤(1??)2?n(I(X;Y)+3?) for sufficiently large $
1.5 Discrete Memoryless Channel (DMC) without feedback
来自于书中的8.5章节

一个消息
W
W
W 首先被编码成长度为
n
n
n 的序列
X
n
X^n
Xn,
X
n
X^n
Xn 是信道的输入, 信道是一概率转移矩阵 (probability transition matrix)
p
(
y
∣
x
)
p(y|x)
p(y∣x), 这里的随机性是由于噪声, 信道的输出是
Y
n
Y^n
Yn,
Y
n
Y^n
Yn 随即被解码成
W
^
\hat{W}
W^.
- Memoryless 表示 p ( y k ∣ x k , y k ? 1 ) = p ( y k ∣ x k ) p(y_k|x^k, y^{k-1})=p(y_{k}|x_k) p(yk?∣xk,yk?1)=p(yk?∣xk?), 即输出的概率分布只依赖于此时刻 ( k k k) 的输入, 与之前的输入输出条件独立.
- W/O Feedback 表示 p ( x k ∣ x k ? 1 , y k ? 1 ) = p ( x k ∣ x k ? 1 ) p(x_k|x^{k-1},y^{k-1})=p(x_k|x^{k-1}) p(xk?∣xk?1,yk?1)=p(xk?∣xk?1), 即输入与之前的输出独立.
- 因此 channel transition function 可以化简为
p ( y n ∣ x n ) = ∏ i = 1 n p ( y i ∣ x i ) p(y^n|x^n) = \prod_{i=1}^{n} p(y_i|x_i) p(yn∣xn)=i=1∏n?p(yi?∣xi?)
接下来是一些重要的定义:
- An
(
M
,
n
)
(M,n)
(M,n) code for channel
(
S
X
,
p
(
y
∣
x
)
,
S
Y
)
(S_X,p(y|x), S_Y)
(SX?,p(y∣x),SY?) consists of:
An index set { 1 , 2 , . . . , M } \{1,2,...,M\} {1,2,...,M},
An encoding function X n : { 1 , 2 , . . . , M } → S X n X^n:\{1,2,...,M\}\rightarrow S_X^n Xn:{1,2,...,M}→SXn?, yielding codewords x n ( 1 ) , x n ( 2 ) , . . . , x n ( M ) x^n(1), x^n(2),..., x^n(M) xn(1),xn(2),...,xn(M). The set of codewords is called the codebook,
A decoding function g : S Y n → { 1 , 2 , . . . , M } g: S_{Y}^n \rightarrow \{1,2,...,M\} g:SYn?→{1,2,...,M}, which is a deterministic function. - The information channel capacity:
C = max ? p ( x ) I ( X ; Y ) C=\max_{p(x)}I(X;Y) C=p(x)max?I(X;Y) - Conditional probability of error:
λ i = Pr ? { g ( Y n ) ≠ i ∣ X n = x n ( i ) } = ∑ y n : g ( y n ) ≠ i p ( y n ∣ x n ( i ) ) \lambda_i=\Pr\{g(Y^n)\neq i|X^n=x^n(i)\}=\sum_{y^n:g(y^n) \neq i} p(y^n|x^n(i)) λi?=Pr{g(Yn)=i∣Xn=xn(i)}=yn:g(yn)=i∑?p(yn∣xn(i)) - The maximal probability of error
λ
(
n
)
\lambda^{(n)}
λ(n) for an
(
M
,
n
)
(M,n)
(M,n) code:
λ ( n ) = max ? i ∈ 1 , . . . , M λ i \lambda^{(n)}=\max_{i\in{1,...,M}}\lambda_i λ(n)=i∈1,...,Mmax?λi? - The arithmetic average probability of error
P
e
(
n
)
Pe^{(n)}
Pe(n) for an
(
M
,
n
)
(M,n)
(M,n) code:
P e ( n ) = 1 M ∑ i = 1 M λ i Pe^{(n)}=\frac{1}{M}\sum_{i=1}^M \lambda_i Pe(n)=M1?i=1∑M?λi? - The rate
R
R
R for an
(
M
,
n
)
(M,n)
(M,n) code:
R = log ? M n R=\frac{\log M}{n} R=nlogM?
单位是 bits/ch. use
2. Channel Coding Theorem
来自于书中的8.7章节
For a discrete memoryless channel, all rates below capacity
C
C
C are achievable. Specifically, for every rate
R
<
C
R < C
R<C, there exists a sequence of
(
2
n
R
,
n
)
(2^{nR}, n)
(2nR,n) codes with maximum probability of error
λ
(
n
)
→
0
\lambda^{(n)} \rightarrow 0
λ(n)→0 as
n
→
∞
n\rightarrow \infty
n→∞.
Conversely, any sequence of
(
2
n
R
,
n
)
(2^{nR}, n)
(2nR,n) codes with
λ
(
n
)
→
0
\lambda^{(n)} \rightarrow 0
λ(n)→0 must have
R
≤
C
R \leq C
R≤C.
针对 DMC, 定理说明了两件事: 1. Achievability: 如果
R
R
R 小于信道容量
C
C
C, 那么存在一种编码技术使
λ
(
n
)
\lambda^{(n)}
λ(n)任意小, 也就是说接收端收到的错误达到任意小的数值; 2. Converse: 任何无错编码技术一定满足
R
≤
C
R \leq C
R≤C.
2.1 证明 Achievability:
固定
p
(
x
)
p(x)
p(x), 首先分析根据
p
(
x
)
p(x)
p(x) 随机生成一个
(
M
,
n
)
(M,n)
(M,n) code 的概率, 这等价于根据
p
(
x
n
)
=
∏
i
=
1
n
p
(
x
i
)
p(x^n)=\prod_{i=1}^n p(x_i)
p(xn)=∏i=1n?p(xi?) 独立生成
2
n
R
2^{nR}
2nR 个 codewords, 这
2
n
R
2^{nR}
2nR 个 codewords即为 codebook
B
B
B. (编码簿)
如果把这个 codebook 写作一个
2
n
R
×
n
2^{nR} \times n
2nR×n 的矩阵:
B
=
[
x
1
(
1
)
x
2
(
1
)
.
.
.
x
n
(
1
)
.
.
.
.
.
.
.
.
.
.
.
.
x
1
(
2
n
R
)
x
2
(
2
n
R
)
.
.
.
x
n
(
2
n
R
)
]
B = \begin{bmatrix} x_1(1) & x_2(1) & ... & x_n(1)\\ ...& ... & ...& ...\\ x_1(2^{nR}) & x_2(2^{nR}) & ... & x_n(2^{nR}) \end{bmatrix}
B=
?x1?(1)...x1?(2nR)?x2?(1)...x2?(2nR)?.........?xn?(1)...xn?(2nR)?
?
每行即为 codewords, 如第一行为
x
n
(
1
)
x^n(1)
xn(1), 是消息
1
1
1 的 codeword, 且
p
(
x
n
(
1
)
)
=
∏
i
=
1
n
p
(
x
i
(
1
)
)
p(x^n(1))=\prod_{i=1}^n p(x_i(1))
p(xn(1))=∏i=1n?p(xi?(1)).
所以, 生成
B
B
B 的概率为
Pr
?
(
B
)
=
∏
w
=
1
2
n
R
∏
i
=
1
n
p
(
x
i
(
w
)
)
\Pr(B)=\prod_{w=1}^{2^{nR}} \prod_{i=1}^n p(x_i(w))
Pr(B)=w=1∏2nR?i=1∏n?p(xi?(w))
考虑以下事件:
- 根据上述概率公式生成一个随机的 codebook B B B.
- 向发送端 Tx 和接收端 Rx 揭示 B, 假设 Tx 和 Rx 已知信道 p ( y ∣ x ) p(y|x) p(y∣x).
- (均匀)随机选择一个消息
w
w
w:
p ( W = w ) = 2 ? n R , w ∈ { 1 , . . . , 2 n R } p(W=w)=2^{-nR}, w\in\{1,...,2^{nR}\} p(W=w)=2?nR,w∈{1,...,2nR} - 通过信道传送 w w w.
- 接收端 Rx 根据 p ( y n ∣ x n ( w ) ) = ∏ i = 1 n p ( y i ∣ x i ( w ) ) p(y^n|x^n(w))=\prod_{i=1}^n p(y_i|x_i(w)) p(yn∣xn(w))=∏i=1n?p(yi?∣xi?(w)) 接收到长度为 n 的序列 Y n Y^n Yn
- 如果下列两个条件成立, 则接收端 Rx 输出
w
^
\hat{w}
w^:
a) ( x n ( w ^ ) , y n ) ∈ A ? ( n ) (x^n(\hat{w}), y^n)\in A_\epsilon^{(n)} (xn(w^),yn)∈A?(n)? .
b) 没有其他的 index k k k 满足 ( x n ( k ) , y n ) ∈ A ? ( n ) (x^n(k), y^n)\in A_\epsilon^{(n)} (xn(k),yn)∈A?(n)? .
如果不存在这样的 w ^ \hat{w} w^ 或者不只有一个这样的 w ^ \hat{w} w^, 那么报错. - 如果 w ^ ≠ w \hat{w} \neq w w^=w, 报错.
接下来分析报错的概率
Pr
?
(
e
)
\Pr(e)
Pr(e):

令
E
i
=
{
(
X
n
(
i
)
,
Y
n
)
∈
A
?
(
n
)
}
E_i=\{(X^n(i), Y^n) \in A_\epsilon^{(n)}\}
Ei?={(Xn(i),Yn)∈A?(n)?}, 其中
Y
n
Y^n
Yn 为信道对
X
n
(
1
)
X^n(1)
Xn(1)的输出, 因为假设了传递的消息
w
=
1
w=1
w=1.
根据6(a), 6(b) 和 7的描述可知, 当传递的codeword与接收到的序列不 jointly typical 时 (等价于
E
1
C
E_1^C
E1C?), 或一个错误的 codeword与接收到的序列是 jointly typical 时(等价于
E
2
∪
E
2
∪
.
.
.
∪
E
2
n
R
E_2 \cup E_2 \cup ... \cup E_{2^{nR}}
E2?∪E2?∪...∪E2nR?), 错误产生. 所以:
Pr
?
(
e
)
=
Pr
?
(
e
∣
W
=
1
)
=
Pr
?
(
E
1
C
∪
E
2
∪
E
3
∪
.
.
.
∪
E
2
n
R
∣
W
=
1
)
\Pr(e) =\Pr(e|W=1)=\Pr(E_1^C\cup E_2 \cup E_3 \cup ... \cup E_{2^{nR}}|W=1)
Pr(e)=Pr(e∣W=1)=Pr(E1C?∪E2?∪E3?∪...∪E2nR?∣W=1)
根据union bound, 上式满足
≤
Pr
?
(
E
1
C
∣
W
=
1
)
+
∑
i
=
2
2
n
R
Pr
?
(
E
i
∣
W
=
1
)
\leq \Pr(E_1^C|W=1)+\sum_{i=2}^{2^{nR}}\Pr(E_i|W=1)
≤Pr(E1C?∣W=1)+i=2∑2nR?Pr(Ei?∣W=1)
根据 joint AEP 的第一条性质, 对于足够大的 n 有
Pr
?
(
E
1
C
∣
W
=
1
)
≤
?
\Pr(E_1^C|W=1)\leq \epsilon
Pr(E1C?∣W=1)≤?.
根据 joint AEP 的最后一条性质, 对于足够大的 n 有
Pr
?
(
E
i
∣
W
=
1
)
≤
2
?
n
(
I
(
X
;
Y
)
?
3
?
)
\Pr(E_i|W=1) \leq 2^{-n (I(X;Y)-3\epsilon)}
Pr(Ei?∣W=1)≤2?n(I(X;Y)?3?), 带入上式
≤
?
+
(
2
n
R
?
1
)
2
?
n
(
I
(
X
;
Y
)
?
3
?
)
≤
?
+
2
?
n
(
I
(
X
;
Y
)
?
3
?
?
R
)
\leq \epsilon +(2^{nR}-1) 2^{-n (I(X;Y)-3\epsilon)}\\ \leq \epsilon +2^{-n (I(X;Y)-3\epsilon -R)}
≤?+(2nR?1)2?n(I(X;Y)?3?)≤?+2?n(I(X;Y)?3??R)
当 n 足够大且
R
<
I
(
X
;
Y
)
?
3
?
R< I(X;Y)-3\epsilon
R<I(X;Y)?3? 时, 上式满足
≤
2
?
\leq 2\epsilon
≤2?
目前已经证明了当
R
<
I
(
X
;
Y
)
?
3
?
R< I(X;Y)-3\epsilon
R<I(X;Y)?3? 时, 我们可以选择合适的
n
n
n 和
?
\epsilon
? 令平均错误率
P
e
(
x
)
Pe^{(x)}
Pe(x) 小于等于
2
?
2\epsilon
2?. 这里的平均是在所有的 codewords 和所有的 codebook 上的平均, 正如图片中的 sum over B 和 sum over w.
但是此时只得到了平均错误率的上界, 无法得出定理中的结论, 接下来推最大错误率
λ
(
n
)
\lambda^{(n)}
λ(n) 的上界.
再次考虑以下事件:
- 选择
p
(
x
)
=
p
?
(
x
)
p(x)=p^*(x)
p(x)=p?(x),
p
?
(
x
)
p^*(x)
p?(x) 为令
I
(
X
;
Y
)
I(X;Y)
I(X;Y) 最大的输入分布, 也就是
p
?
(
x
)
p^*(x)
p?(x) 是实现通道容量的那个分布.
所以上面的条件 R < I ( X ; Y ) ? R < C R< I(X;Y) \Rightarrow R<C R<I(X;Y)?R<C . - 选择一个平均错误率最小的 codebook
B
?
B*
B?, 所以
Pr ? ( e ∣ B ? ) = 1 2 n R ∑ i = 1 2 n R λ i ( B ? ) ≤ 2 ? \Pr(e|B*)=\frac{1}{2^{nR}} \sum_{i=1}^{2^{nR}} \lambda_i (B* )\leq 2\epsilon Pr(e∣B?)=2nR1?i=1∑2nR?λi?(B?)≤2? - 移除 B ? B^{*} B? 中最差的那半 codewords, 将剩余部分记为 B ? ? B^{**} B??, 由于平均错误率小于等于 2 ? 2\epsilon 2? 且 概率是非负的, 所以 B ? ? B^{**} B??的最大错误率一定小于等于 4 ? 4\epsilon 4?, 否则上一条中的不等式将不成立.
Achievability 证明完毕.
其中, 移除一半codewords 令 index set 减少一半, 即
2
n
R
→
2
n
R
×
1
2
=
2
n
(
R
?
1
n
)
2^{nR} \rightarrow 2^{nR}\times \frac{1}{2}=2^{n(R-\frac{1}{n})}
2nR→2nR×21?=2n(R?n1?)
速率 R 只减少了
1
n
\frac{1}{n}
n1?, 且当 n 很大时, 对 R 几乎无影响.
2.2 证明 Converse:
来自于书中的8.8 - 8.10章节
未完待续
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!