数据结构-十大排序算法
数据结构十大排序算法
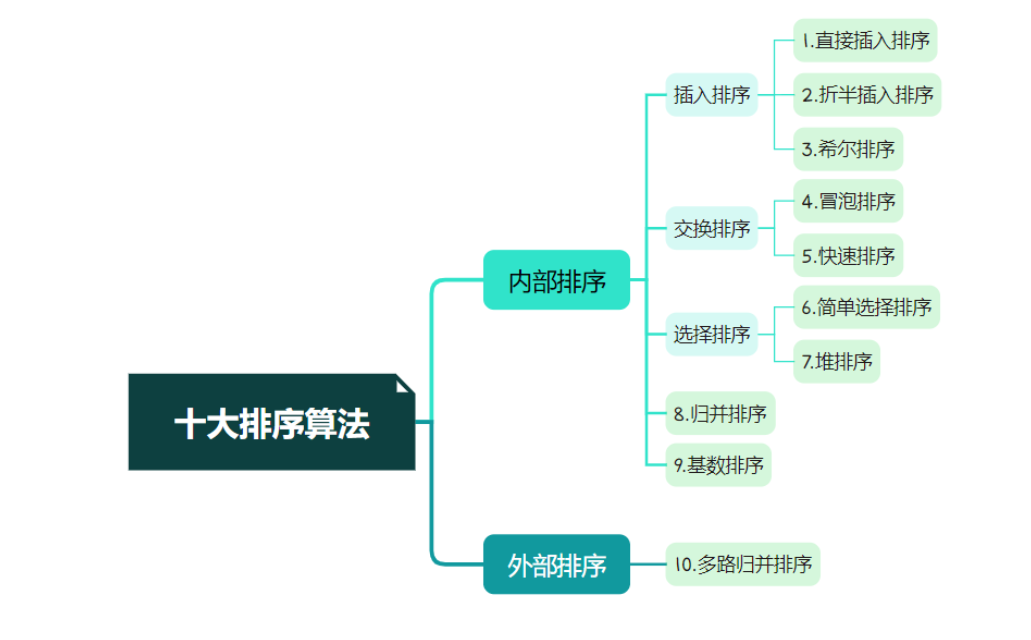
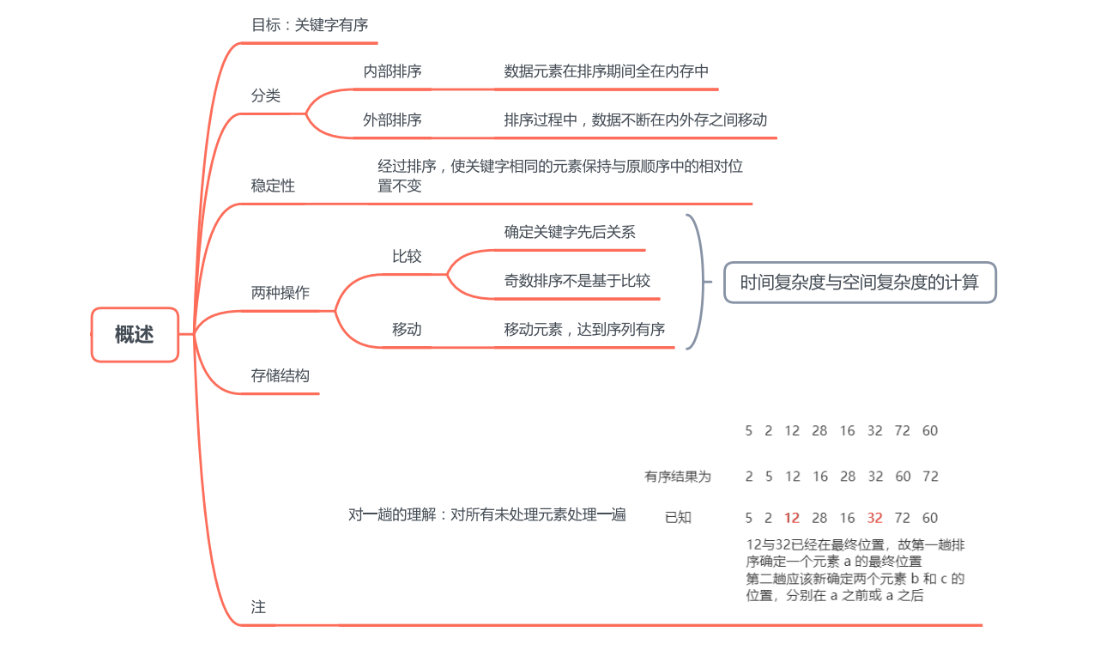
十大排序算法分别是直接插入排序、折半插入排序、希尔排序、冒泡排序、快速排序、简单选择排序、堆排序、归并排序、基数排序、外部排序。
其中插入排序包括直接插入排序、折半插入排序、希尔排序;交换排序包括冒泡排序、快速排序;选择排序包括简单选择排序、堆排序
1. 直接插入排序
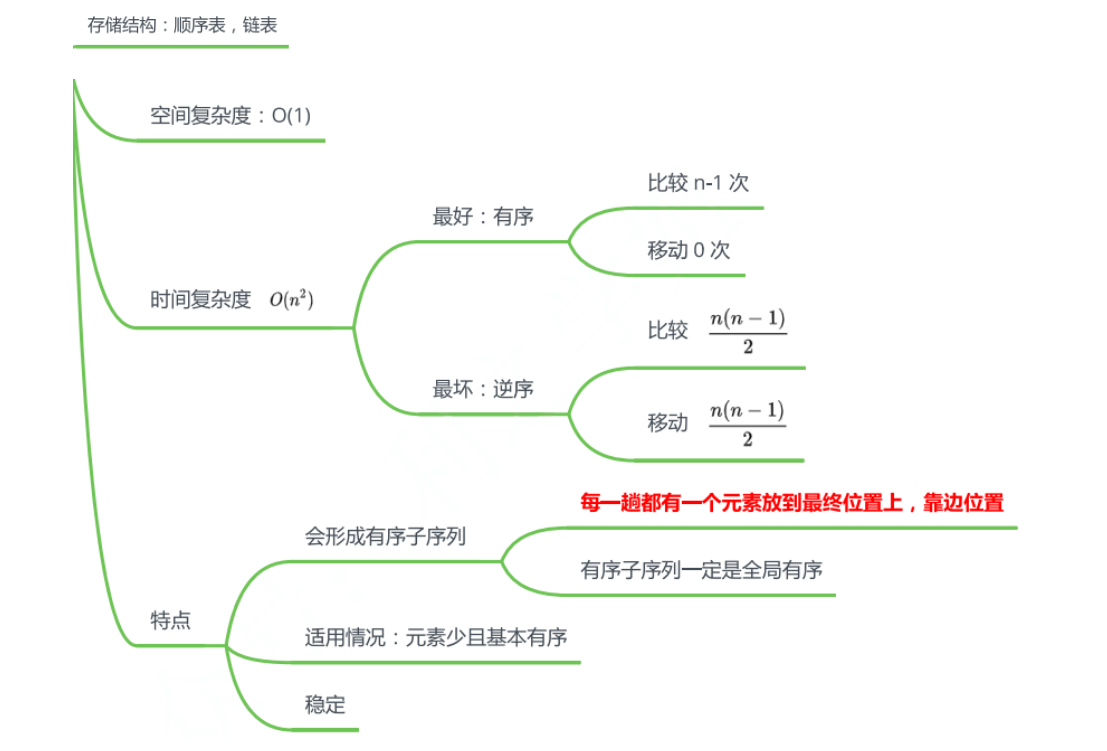
直接插入排序(Insertion Sort)是一种简单的排序算法,它的基本思想是将待排序的元素逐个插入已经有序的部分序列中,从而得到一个有序的序列。
下面是直接插入排序的步骤:
- 假设要对一个数组进行升序排序,从第二个元素开始,将其作为当前元素。
- 将当前元素与已排序的部分序列进行比较,找到合适的位置插入当前元素。如果当前元素小于已排序部分的某个元素,就将这个元素后移一位,直到找到合适的位置。
- 将当前元素插入到合适的位置。
- 重复步骤 2 和步骤 3,直到所有元素都被插入到合适的位置。
以下是使用 C 实现的直接插入排序的示例代码:

void insertionSort(int arr[], int n) {
int i, j, current;
for (i = 1; i < n; i++) {
current = arr[i];
j = i - 1;
while (j >= 0 && arr[j] > current) {
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = current;
}
}
2.折半插入排序
折半插入排序(Binary Insertion Sort)是对直接插入排序算法的改进,通过利用二分查找的方式来寻找插入位置,减少了比较的次数,从而提高了排序的效率。
下面是折半插入排序的步骤:
- 假设要对一个数组进行升序排序,从第二个元素开始,将其作为当前元素。
- 将当前元素与已排序的部分序列的中间元素进行比较,确定插入位置的范围。
- 使用二分查找在确定的范围内找到合适的位置插入当前元素。
- 将当前元素插入到合适的位置。
- 重复步骤 2 到步骤 4,直到所有元素都被插入到合适的位置。
以下是使用 C 语言实现折半插入排序的示例代码:
void binaryInsertionSort(int arr[], int n) {
int i, j, current, low, high, mid;
for (i = 1; i < n; i++) {
current = arr[i];
low = 0;
high = i - 1;
// 使用二分查找确定插入位置的范围
while (low <= high) {
mid = (low + high) / 2;
if (arr[mid] > current)
high = mid - 1;
else
low = mid + 1;
}
// 插入当前元素到合适的位置
for (j = i - 1; j >= low; j--) {
arr[j + 1] = arr[j];
}
arr[low] = current;
}
}
3.希尔排序
希尔排序(Shell Sort)是一种改进的插入排序算法,它通过比较和交换相隔一定间隔的元素,逐步减小间隔,最终使整个序列达到有序状态。
下面是希尔排序的步骤:
- 首先选择一个间隔序列(增量序列),通常使用 Knuth 序列或者 Hibbard 序列。这些序列中的元素逐步减小,最后一个元素为 1。
- 对于每个间隔,将数组分为多个子序列,分别对这些子序列进行插入排序。
- 逐步减小间隔,重复步骤 2,直到间隔为 1。
- 最后进行一次间隔为 1 的插入排序,完成整个排序过程。
以下是使用 C 语言实现希尔排序的示例代码:


#include <stdio.h>
void shellSort(int arr[], int n) {
int gap, i, j, temp;
// 使用 Knuth 序列计算初始间隔
gap = 1;
while (gap < n / 3) {
gap = gap * 3 + 1;
}
while (gap > 0) {
for (i = gap; i < n; i++) {
temp = arr[i];
j = i;
while (j > gap - 1 && arr[j - gap] > temp) {
arr[j] = arr[j - gap];
j -= gap;
}
arr[j] = temp;
}
// 缩小间隔
gap = (gap - 1) / 3;
}
}
// 示例用法
int main() {
int arr[] = {5, 2, 8, 1, 3};
int n = sizeof(arr) / sizeof(arr[0]);
shellSort(arr, n);
printf("Sorted array: ");
for (int i = 0; i < n; i++) {
printf("%d ", arr[i]);
}
printf("\n");
return 0;
}
4.冒泡排序
冒泡排序(Bubble Sort)是一种简单的排序算法,它重复地比较相邻的两个元素,并交换顺序不正确的元素,直到整个序列排序完成。
下面是冒泡排序的步骤:
- 从序列的第一个元素开始,比较该元素与下一个元素的大小。
- 如果当前元素大于下一个元素,则交换它们的位置。
- 继续向后比较相邻的元素,重复步骤 2,直到遍历到倒数第二个元素。
- 重复步骤 1 到步骤 3,直到没有需要交换的元素,即序列已经排序完成。
以下是使用 C 语言实现冒泡排序的示例代码:

void bubbleSort(int arr[], int n) {
int i, j, temp;
for (i = 0; i < n - 1; i++) {
for (j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
// 交换元素
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
5.快速排序
快速排序(Quick Sort)是一种高效的排序算法,它基于分治的思想,通过将数组分成较小的子数组,然后递归地对子数组进行排序,最终将整个数组排序。
以下是快速排序的步骤:
- 选择一个元素作为基准(通常选择数组的第一个元素)。
- 将数组分成两个子数组,比基准小的元素放在左边,比基准大的元素放在右边。
- 对左右两个子数组递归地执行步骤 1 和步骤 2,直到子数组的长度为 0 或 1,表示已经排序完成。
- 合并排序后的子数组,得到最终的排序结果。
以下是使用 C 语言实现快速排序的示例代码:



// 交换两个元素的值
void swap(int* a, int* b) {
int temp = *a;
*a = *b;
*b = temp;
}
// 将数组分成左右两个子数组,并返回基准元素的最终位置
int partition(int arr[], int low, int high) {
int pivot = arr[low]; // 选择第一个元素作为基准
int i = low + 1;
int j = high;
while (1) {
// 在左侧找到第一个大于基准的元素的位置
while (i <= j && arr[i] < pivot) {
i++;
}
// 在右侧找到第一个小于基准的元素的位置
while (j >= i && arr[j] > pivot) {
j--;
}
// 若两个指针相遇或交错,则跳出循环
if (i >= j) {
break;
}
// 交换元素,使小于基准的元素在左侧,大于基准的元素在右侧
swap(&arr[i], &arr[j]);
i++;
j--;
}
// 将基准元素放到最终的位置
swap(&arr[low], &arr[j]);
// 返回基准元素的位置
return j;
}
// 执行快速排序算法
void quickSort(int arr[], int low, int high) {
if (low < high) {
// 划分子数组,并获取基准元素的位置
int pivotIndex = partition(arr, low, high);
// 对左侧子数组进行快速排序
quickSort(arr, low, pivotIndex - 1);
// 对右侧子数组进行快速排序
quickSort(arr, pivotIndex + 1, high);
}
}
6.简单选择排序
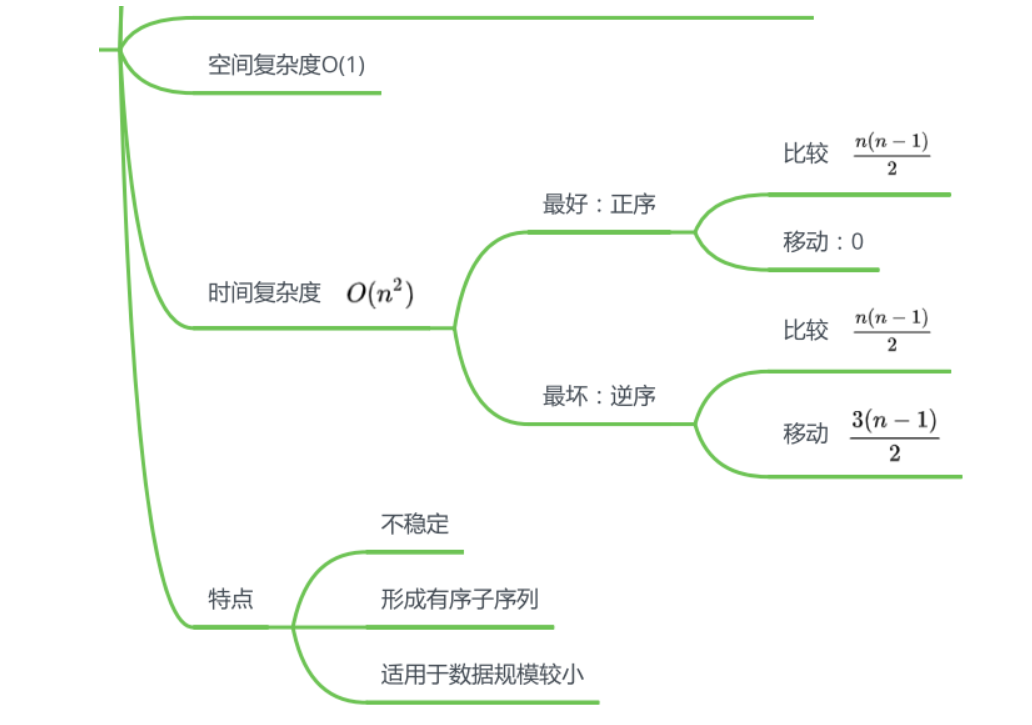
简单选择排序(Selection Sort)是一种简单直观的排序算法,它每次从未排序的部分选择最小(或最大)的元素,并将其放到已排序部分的末尾。
以下是简单选择排序的步骤:
- 在未排序部分中,找到最小(或最大)的元素。
- 将最小(或最大)的元素与未排序部分的第一个元素交换位置。
- 将已排序部分的末尾向后扩展一个位置。
- 重复步骤 1 到步骤 3,直到未排序部分为空。
以下是使用 C 语言实现简单选择排序的示例代码:

void swap(int* a, int* b) {
int temp = *a;
*a = *b;
*b = temp;
}
void selectionSort(int arr[], int n) {
int i, j, minIndex;
for (i = 0; i < n - 1; i++) {
minIndex = i;
for (j = i + 1; j < n; j++) {
if (arr[j] < arr[minIndex]) {
minIndex = j;
}
}
swap(&arr[i], &arr[minIndex]);
}
}
7.堆排序
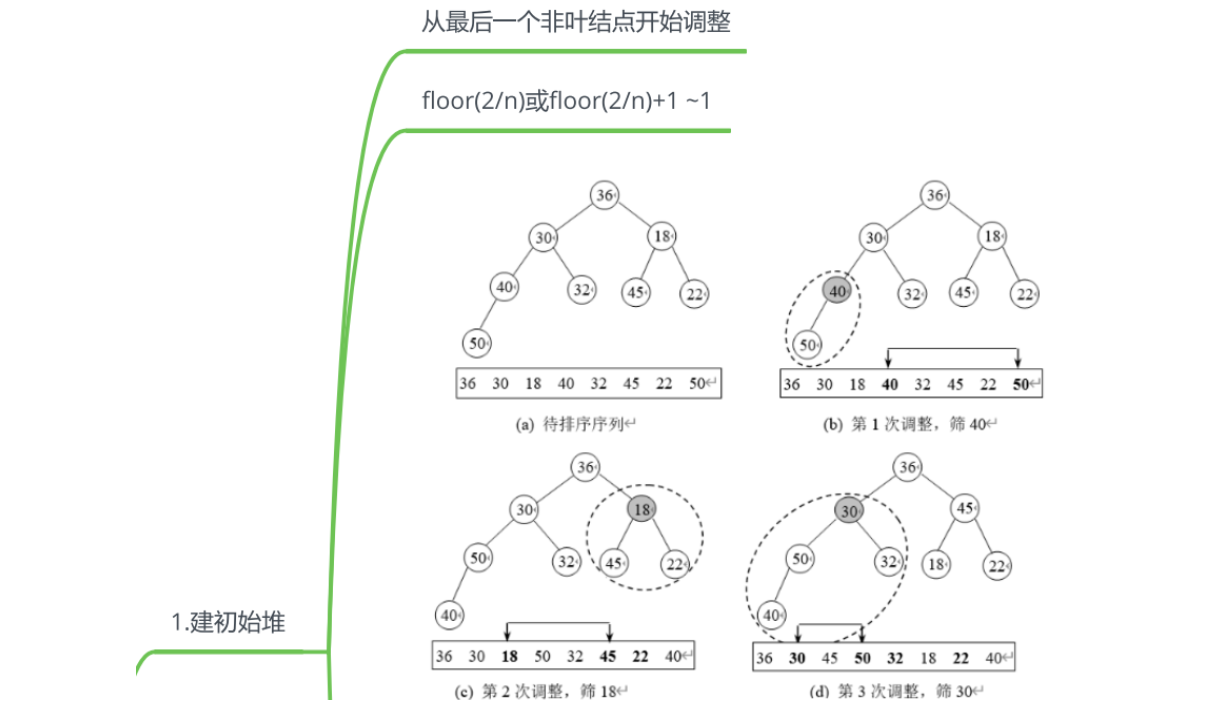
堆排序(Heap Sort)是一种基于堆数据结构的排序算法,它利用堆的性质进行排序。堆排序分为两个步骤:建堆和排序。
以下是堆排序的步骤:
- 建堆(Heapify):将待排序的数组构建成一个堆结构。堆是一个完全二叉树,其中每个节点的值都大于等于(或小于等于)其子节点的值,这被称为最大堆(或最小堆)的性质。
- 排序:将堆顶元素与最后一个叶节点交换,并从根节点开始调整堆,使其满足堆的性质。然后再次将堆顶元素与倒数第二个叶节点交换,再次调整堆。重复这个过程,直到堆中剩下一个元素为止。
以下是使用 C 语言实现堆排序的示例代码:


// 交换两个元素的值
void swap(int* a, int* b) {
int temp = *a;
*a = *b;
*b = temp;
}
// 对以rootIndex为根节点的子树进行堆调整,n为堆的大小
void heapify(int arr[], int n, int rootIndex) {
int largest = rootIndex; // 最大元素的索引
int leftChild = 2 * rootIndex + 1; // 左子节点的索引
int rightChild = 2 * rootIndex + 2; // 右子节点的索引
// 找出左右子节点和根节点中的最大元素
if (leftChild < n && arr[leftChild] > arr[largest]) {
largest = leftChild;
}
if (rightChild < n && arr[rightChild] > arr[largest]) {
largest = rightChild;
}
// 如果最大元素不是根节点,则交换根节点和最大元素,并递归调整交换后的子树
if (largest != rootIndex) {
swap(&arr[rootIndex], &arr[largest]);
heapify(arr, n, largest);
}
}
// 堆排序
void heapSort(int arr[], int n) {
// 构建最大堆,从最后一个非叶节点开始向上调整
for (int i = n / 2 - 1; i >= 0; i--) {
heapify(arr, n, i);
}
// 依次将堆顶元素与末尾元素交换,并重新调整堆
for (int i = n - 1; i >= 0; i--) {
swap(&arr[0], &arr[i]);
heapify(arr, i, 0);
}
}
在上述代码中,我们定义了一个辅助函数 swap,用于交换两个元素的值。
然后,我们定义了 heapify 函数来进行堆调整,以满足堆的性质。
接下来,我们定义了 heapSort 函数来执行堆排序算法。在该函数中,我们首先构建一个最大堆,然后依次将堆顶元素与末尾元素交换,并重新调整堆。
8.归并排序
归并排序(Merge Sort)是一种基于分治思想的排序算法。它将待排序的数组分成两个子数组,分别进行排序,然后将排序后的子数组合并成一个有序数组。归并排序的关键步骤是合并(Merge)操作,通过将两个有序的子数组合并成一个有序数组来实现排序。
以下是归并排序的步骤:
- 分解:将待排序的数组递归地分解成两个子数组,直到每个子数组只剩下一个元素或为空。
- 合并:将两个有序的子数组合并成一个有序数组。合并过程中,依次比较两个子数组的元素,将较小(或较大)的元素放入临时数组中,并更新索引,直到其中一个子数组的所有元素都放入临时数组中。将剩余的元素依次放入临时数组中。
- 返回合并后的有序数组。
以下是使用 C 语言实现归并排序的示例代码:


#include <stdio.h>
#include <stdlib.h>
// 合并两个有序子数组为一个有序数组
void merge(int arr[], int left, int mid, int right) {
int n1 = mid - left + 1; // 左子数组的元素个数
int n2 = right - mid; // 右子数组的元素个数
// 创建临时数组来存储两个子数组的元素
int* leftArr = (int*)malloc(n1 * sizeof(int));
int* rightArr = (int*)malloc(n2 * sizeof(int));
// 将元素复制到临时数组中
for (int i = 0; i < n1; i++) {
leftArr[i] = arr[left + i];
}
for (int j = 0; j < n2; j++) {
rightArr[j] = arr[mid + 1 + j];
}
// 合并两个子数组为一个有序数组
int i = 0; // 左子数组的索引
int j = 0; // 右子数组的索引
int k = left; // 合并后数组的索引
while (i < n1 && j < n2) {
if (leftArr[i] <= rightArr[j]) {
arr[k] = leftArr[i];
i++;
} else {
arr[k] = rightArr[j];
j++;
}
k++;
}
// 将剩余的元素放入合并后的数组中
while (i < n1) {
arr[k] = leftArr[i];
i++;
k++;
}
while (j < n2) {
arr[k] = rightArr[j];
j++;
k++;
}
// 释放临时数组的内存
free(leftArr);
free(rightArr);
}
// 归并排序递归函数
void mergeSort(int arr[], int left, int right) {
if (left < right) {
int mid = left + (right - left) / 2; // 计算中间索引
// 递归地对左右子数组进行排序
mergeSort(arr, left, mid);
mergeSort(arr, mid + 1, right);
// 合并两个有序子数组
merge(arr, left, mid, right);
}
}
// 示例用法
int main() {
int arr[] = {5, 2, 8, 1, 3};
int n = sizeof(arr) / sizeof(arr[0]);
mergeSort(arr, 0, n - 1);
printf("Sorted array: ");
for (int i = 0; i < n; i++) {
printf("%d ", arr[i]);
}
printf("\n");
return 0;
}
在上述代码中,我们定义了 merge 函数,用于合并两个有序子数组。该函数接受数组 arr、左子数组的起始索引 left、中间索引 mid 和右子数组的结束索引 right。
然后,我们定义了 mergeSort 函数来执行归并排序算法。该函数采用分治的思想,首先递归地对左右子数组进行排序,然后调用 merge 函数合并两个有序子数组。
9.基数排序
基数排序(Radix Sort)是一种非比较型的排序算法,它根据元素的位数进行排序。基数排序逐位比较元素,从最低有效位(LSB)到最高有效位(MSB)进行排序。在每一位上,使用稳定的排序算法(如计数排序或桶排序)对元素进行排序。通过重复这个过程,直到对所有位都完成排序,最终得到一个有序的数组。
以下是基数排序的步骤:
- 获取数组中最大元素的位数(最大元素的位数决定了排序的轮数)。
- 对每一位进行排序:
- 使用稳定的排序算法对当前位进行排序(例如计数排序或桶排序)。
- 根据当前位的值将元素放入对应的桶中。
- 将桶中的元素按照顺序取出,更新原数组。
- 重复步骤 2 直到对所有位都完成排序。
以下是使用 C 语言实现基数排序的示例代码,使用计数排序作为稳定的排序算法:
#include <stdio.h>
// 获取数组中的最大元素
int getMax(int arr[], int n) {
int max = arr[0];
for (int i = 1; i < n; i++) {
if (arr[i] > max) {
max = arr[i];
}
}
return max;
}
// 使用计数排序对数组按照指定的位进行排序
void countSort(int arr[], int n, int exp) {
const int MAX_RANGE = 10; // 桶的范围,0-9
int output[n]; // 存储排序结果的临时数组
int count[MAX_RANGE] = {0};
// 统计当前位上每个数字的出现次数
for (int i = 0; i < n; i++) {
count[(arr[i] / exp) % 10]++;
}
// 计算每个数字在排序后的数组中的起始索引
for (int i = 1; i < MAX_RANGE; i++) {
count[i] += count[i - 1];
}
// 将元素按照当前位的值放入临时数组中,同时更新 count 数组
for (int i = n - 1; i >= 0; i--) {
output[count[(arr[i] / exp) % 10] - 1] = arr[i];
count[(arr[i] / exp) % 10]--;
}
// 将临时数组的元素复制回原数组
for (int i = 0; i < n; i++) {
arr[i] = output[i];
}
}
// 基数排序
void radixSort(int arr[], int n) {
int max = getMax(arr, n); // 获取最大元素
// 对每一位进行排序
for (int exp = 1; max / exp > 0; exp *= 10) {
countSort(arr, n, exp);
}
}
在上述代码中,我们定义了 getMax 函数,用于获取数组中的最大元素。
然后,我们定义了 countSort 函数,用于对数组按照指定的位进行排序。该函数采用计数排序算法,在每一位上统计元素的出现次数,然后根据当前位的值将元素放入对应的桶中,并更新原数组。
接下来,我们定义了 radixSort 函数来执行基数排序算法。该函数通过循环对每一位进行排序,调用 countSort 函数。
10.外部排序
外部排序(External Sorting)是一种用于处理大规模数据的排序算法,其中数据量大于计算机内存的容量。外部排序通常涉及将数据分割成较小的块,然后在内存中对这些块进行排序,并最终将它们合并为一个有序的结果。
以下是一种常见的外部排序算法:多路归并排序(Multiway Merge Sort)。
多路归并排序的基本思想是将大型数据集分割成更小的块(通常是内存可容纳的大小),在内存中对这些块进行排序,然后使用归并操作将它们合并成一个有序的结果。
以下是多路归并排序的步骤:
- 将大型数据集划分为较小的块,每个块可以适应内存容量。可以使用外部缓存或者分割文件为固定大小的块来实现。
- 将每个块加载到内存中,并使用内部排序算法(如快速排序、归并排序等)对块进行排序。
- 创建一个输出文件作为最终的有序结果。
- 从每个块中读取一部分数据到内存中(通常是一个块的大小),选择最小的元素,将其写入输出文件。
- 如果块中的数据被消耗完,从该块所在的文件中读取下一块数据到内存中。
- 重复步骤 4 和步骤 5,直到所有块中的数据都被处理。
- 关闭输出文件,排序完成。
需要注意的是,多路归并排序需要使用外部存储器(例如磁盘)来存储和处理大量数据,因此算法的性能会受到外部存储器的读写速度的限制。
实际的外部排序算法中,还会考虑更复杂的策略,如缓冲区管理、归并策略等,以提高排序的效率和性能。
外部排序是一种常用的处理大规模数据的排序方法,在处理海量数据、大型数据库等场景中有广泛的应用。



本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!