机器学习中的特征工程

1 特征工程概述

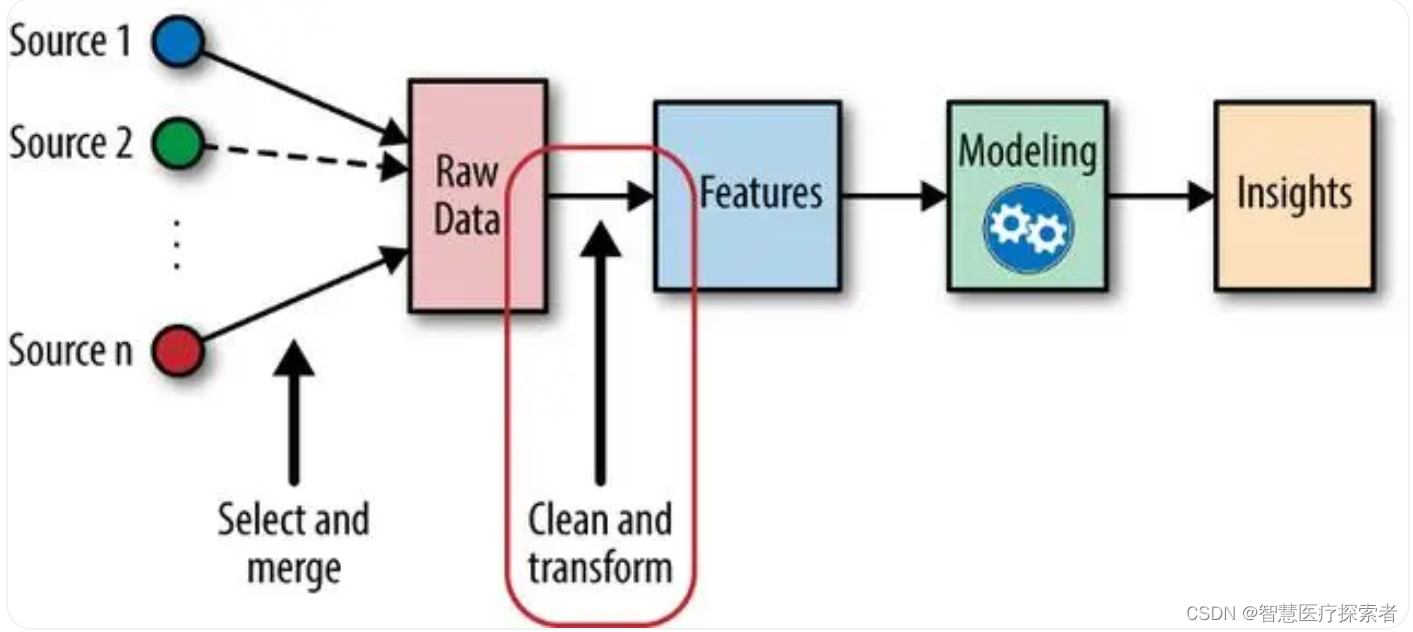
特征工程是机器学习中的一个关键步骤，在机器学习领域中占有非常重要的地位，是机器学习中不可或缺的一部分，下图展示了一个常规的机器学习流程：

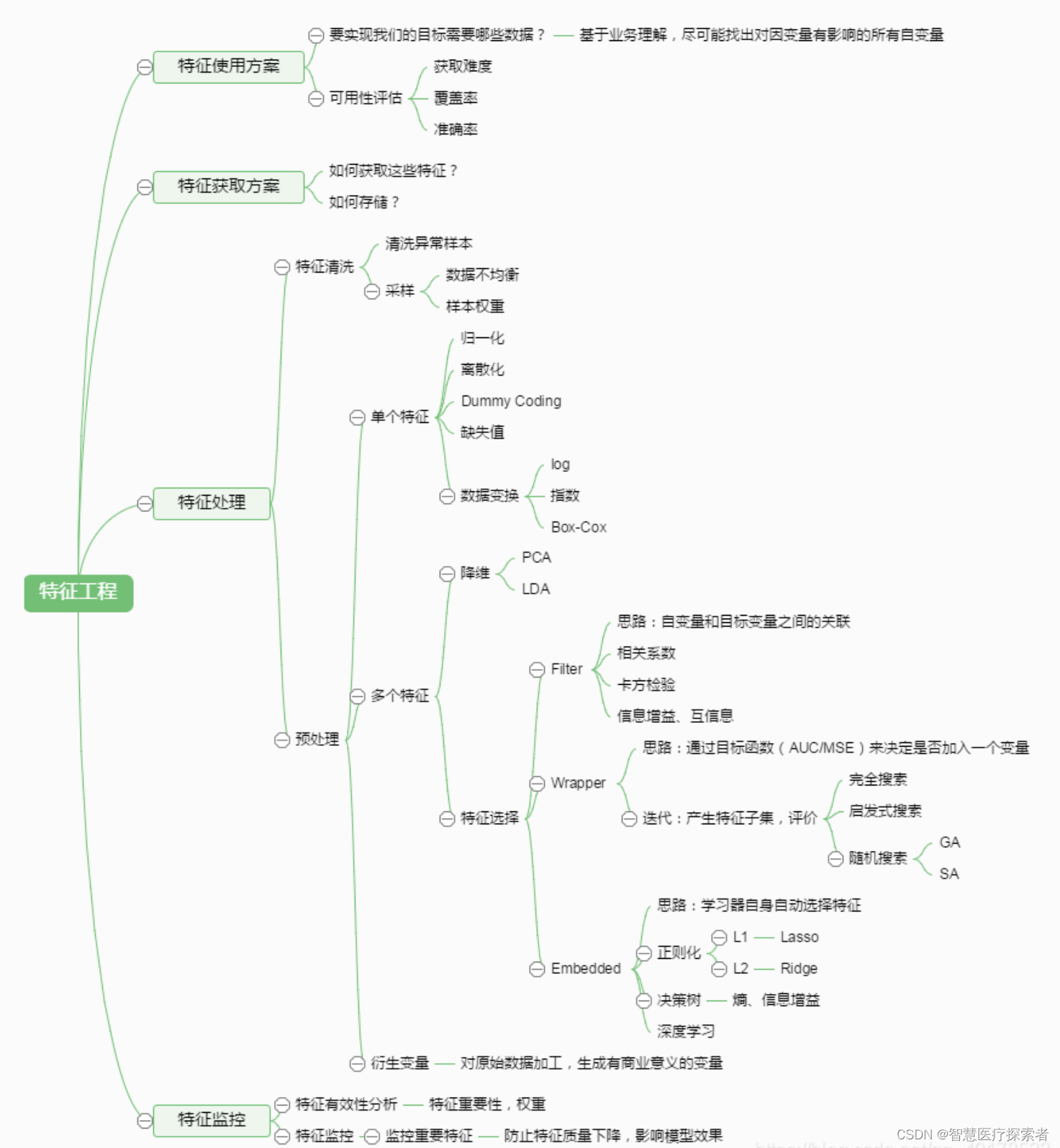
特征工程涉及从原始数据中提取、选择和转换特征，以改善模型的性能。特征工程对于构建有效的机器学习模型至关重要，因为模型的质量和性能很大程度上取决于输入数据的质量。特征工程通常包括特征选择、数据预处理、降维等环节。如下图所示：

1.1 定义

• 特征工程（Feature Engineering）特征工程是将原始数据转化成更好的表达问题本质的特征的过程，使得将这些特征运用到预测模型中能提高对不可见数据的模型预测精度。

• 特征工程简单讲就是发现对因变量y有明显影响作用的特征，通常称自变量x为特征，特征工程的目的是发现重要特征。

• 如何能够分解和聚合原始数据，以更好的表达问题的本质？这是做特征工程的目的。 “feature engineering is manually designing what the input x’s should be.” “you have to turn your inputs into things the algorithm can understand.”

• 特征工程是数据挖掘模型开发中最耗时、最重要的一步。

1.2 意义

• 特征工程是一个包含内容很多的主题，也被认为是成功应用机器学习的一个很重要的环节。如何充分利用数据进行预测建模就是特征工程要解决的问题！ “实际上，所有机器学习算法的成功取决于如何呈现数据。” “特征工程是一个看起来不值得在任何论文或者书籍中被探讨的一个主题。但是他却对机器学习的成功与否起着至关重要的作用。机器学习算法很多都是由于建立一个学习器能够理解的工程化特征而获得成功的。”——ScottLocklin，in “Neglected machine learning ideas”

• 数据中的特征对预测的模型和获得的结果有着直接的影响。可以这样认为，特征选择和准备越好，获得的结果也就越好。这是正确的，但也存在误导。预测的结果其实取决于许多相关的属性：比如说能获得的数据、准备好的特征以及模型的选择。

2 特征选择

当数据预处理完成后，我们需要选择有意义的特征输入机器学习的算法和模型进行训练。不同的特征对模型的影响程度不同，我们要自动地选择出对问题重要的一些特征，移除与问题相关性不是很大的特征，这个过程就叫做特征选择。特征的选择在特征工程中十分重要，往往可以直接决定最后模型训练效果的好坏。

通常来说，从两个方面考虑来选择特征：特征是否发散：如果一个特征不发散，例如方差接近于0，也就是说样本在这个特征上基本上没有差异，这个特征对于样本的区分并没有什么用。特征与目标的相关性：这点比较显见，与目标相关性高的特征，应当优选选择。

常用的特征选择方法有：过滤式（filter）、包裹式（wrapper）、嵌入式（embedding)。

2.1 过滤式

过滤式特征选择是通过评估每个特征和结果的相关性，来对特征进行筛选，留下相关性最强的几个特征。核心思想是：先对数据集进行特征选择，然后再进行模型的训练。过滤式特征选择的优点是思路简单，往往通过Pearson相关系数法、方差选择法、互信息法等方法计算相关性，然后保留相关性最强的N个特征，就可以交给模型训练；缺点是没有考虑到特征与特征之间的相关性，从而导致模型最后的训练效果没那么好。

2.2 包裹式

包裹式特征选择是把最终要使用的机器学习模型、评测性能的指标作为特征选择的重要依据，每次去选择若干特征，或是排除若干特征。通常包裹式特征选择要比过滤式的效果更好，但由于训练过程时间久，系统的开销也更大。最典型的包裹型算法为递归特征删除算法，其原理是使用一个基模型（如：随机森林、逻辑回归等）进行多轮训练，每轮训练结束后，消除若干权值系数较低的特征，再基于新的特征集进行新的一轮训练。

2.3 嵌入式

嵌入式特征选择法是根据机器学习的算法、模型来分析特征的重要性，从而选择最重要的N个特征。与包裹式特征选择法最大的不同是，嵌入式方法是将特征选择过程与模型的训练过程结合为一体，这样就可以快速地找到最佳的特征集合，更加高效、快捷。常用的嵌入式特征选择方法有基于正则化项（如：L1正则化）的特征选择法和基于树模型的特征选择法（如：GBDT）。

在选择特征时，还包含如下方法：

• 组合特征： 结合两个或多个特征，创建新的特征，以捕捉数据中的复杂关系。

• 基于领域知识的特征构造： 利用专业知识构建更具表现力的特征。

?

3 数据预处理

数据预处理是特征工程中最为重要的一个环节，良好的数据预处理可以使模型的训练达到事半功倍的效果。数据预处理旨在通过归一化、标准化、正则化等方式改进不完整、不一致、无法直接使用的数据。通过特征提取，我们能得到未经处理的特征，这时的特征可能有以下问题：

• 不属于同一量纲：即特征的规格不一样，不能够放在一起比较。无量纲化可以解决这一问题。

• 信息冗余：对于某些定量特征，其包含的有效信息为区间划分，例如学习成绩，假若只关心“及格”或不“及 格”，那么需要将定量的考分，转换成“1”和“0”表示及格和未及格。二值化可以解决这一问题。

• 定性特征不能直接使用：某些机器学习算法和模型只能接受定量特征的输入，那么需要将定性特征转换为定 量特征。最简单的方式是为每一种定性值指定一个定量值，但是这种方式过于灵活，增加了调参的工作。通 常使用哑编码的方式将定性特征转换为定量特征：假设有N种定性值，则将这一个特征扩展为N种特征，当原 始特征值为第i种定性值时，第i个扩展特征赋值为1，其他扩展特征赋值为0。哑编码的方式相比直接指定的方 式，不用增加调参的工作，对于线性模型来说，使用哑编码后的特征可达到非线性的效果。

• 存在缺失值：缺失值需要补充。

• 信息利用率低：不同的机器学习算法和模型对数据中信息的利用是不同的，之前提到在线性模型中，使用对 定性特征哑编码可以达到非线性的效果。类似地，对定量变量多项式化，或者进行其他的转换，都能达到非 线性的效果。
  我们使用sklearn中的preproccessing库来进行数据预处理，可以覆盖以上问题的解决方案

数据预处理具体方法如下：

3.1 归一化

归一化是对数据集进行区间缩放，缩放到[0,1]的区间内，把有单位的数据转化为没有单位的数据，即统一数据的衡量标准，消除单位的影响。这样方便了数据的处理，使数据处理更加快速、敏捷。Skearn中最常用的归一化的方法是：MinMaxScaler。此外还有对数函数转换（log），反余切转换等。

3.2 标准化

标准化是在不改变原数据分布的前提下，将数据按比例缩放，使之落入一个限定的区间，使数据之间具有可比性。但当个体特征太过或明显不遵从高斯正态分布时，标准化表现的效果会比较差。标准化的目的是为了方便数据的下一步处理，比如：进行的数据缩放等变换。常用的标准化方法有z-score标准化、StandardScaler标准化等。

3.3 离散化

离散化是把连续型的数值型特征分段，每一段内的数据都可以当做成一个新的特征。具体又可分为等步长方式离散化和等频率的方式离散化，等步长的方式比较简单，等频率的方式更加精准，会跟数据分布有很大的关系。 代码层面，可以用pandas中的cut方法进行切分。总之，离散化的特征能够提高模型的运行速度以及准确率。

3.4 二值化

特征的二值化处理是将数值型数据输出为布尔类型。其核心在于设定一个阈值，当样本书籍大于该阈值时，输出为1，小于等于该阈值时输出为0。我们通常使用preproccessing库的Binarizer类对数据进行二值化处理。

3.5 哑编码

我们针对类别型的特征，通常采用哑编码（One_Hot Encodin）的方式。所谓的哑编码，直观的讲就是用N个维度来对N个类别进行编码，并且对于每个类别，只有一个维度有效，记作数字1 ；其它维度均记作数字0。但有时使用哑编码的方式，可能会造成维度的灾难，所以通常我们在做哑编码之前，会先对特征进行Hash处理，把每个维度的特征编码成词向量。

以上为大家介绍了几种较为常见、通用的数据预处理方式，但只是浩大特征工程中的冰山一角。往往很多特征工程的方法需要我们在项目中不断去总结积累比如：针对缺失值的处理，在不同的数据集中，用均值填充、中位数填充、前后值填充的效果是不一样的；对于类别型的变量，有时我们不需要对全部的数据都进行哑编码处理；对于时间型的变量有时我们有时会把它当作是离散值，有时会当成连续值处理等。所以很多情况下，我们要根据实际问题，进行不同的数据预处理。

?

4 数据降维

如果拿特征选择后的数据直接进行模型的训练，由于数据的特征矩阵维度大，可能会存在数据难以理解、计算量增大、训练时间过长等问题，因此我们要对数据进行降维。降维是指把原始高维空间的特征投影到低维度的空间，进行特征的重组，以减少数据的维度。降维与特征最大的不同在于，特征选择是进行特征的剔除、删减，而降维是做特征的重组构成新的特征，原始特征全部“消失”了，性质发生了根本的变化。常见的降维方法有：主成分分析法（PCA）和线性判别分析法（LDA）。

4.1 主成分分析法

主成分分析法（PCA）是最常见的一种线性降维方法，其要尽可能在减少信息损失的前提下，将高维空间的数据映射到低维空间中表示，同时在低维空间中要最大程度上的保留原数据的特点。主成分分析法本质上是一种无监督的方法，不用考虑数据的类标，它的基本步骤大致如下：

• 数据中心化（每个特征维度减去相应的均值）

• 计算协方差矩阵以及它的特征值和特征向量

• 将特征值从大到小排序并保留最上边的N个特征

• 将高维数据转换到上述N个特征向量构成的新的空间中

此外，在把特征映射到低维空间时要注意，每次要保证投影维度上的数据差异性最大（也就是说投影维度的方差最大）。

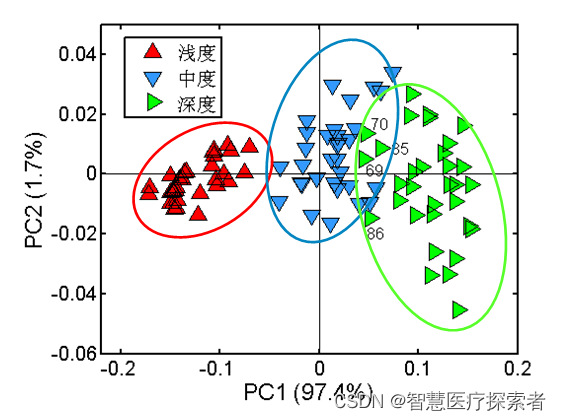
算法详见：https://blog.csdn.net/lsb2002/article/details/131815123

4.2 线性判别分析法

线性判别分析法（LDA）也是一种比较常见的线性降维方法，但不同于PCA的是，它是一种有监督的算法，也就是说它数据集的每个样本会有一个输出类标。线性判别算法的核心思想是，在把数据投影到低维空间后，希望同一种类别数据的投影点尽可能的接近，而不同类别数据的类别中心之间的距离尽可能的远。也就是说LDA是想让降维后的数据点尽可能地被区分开。

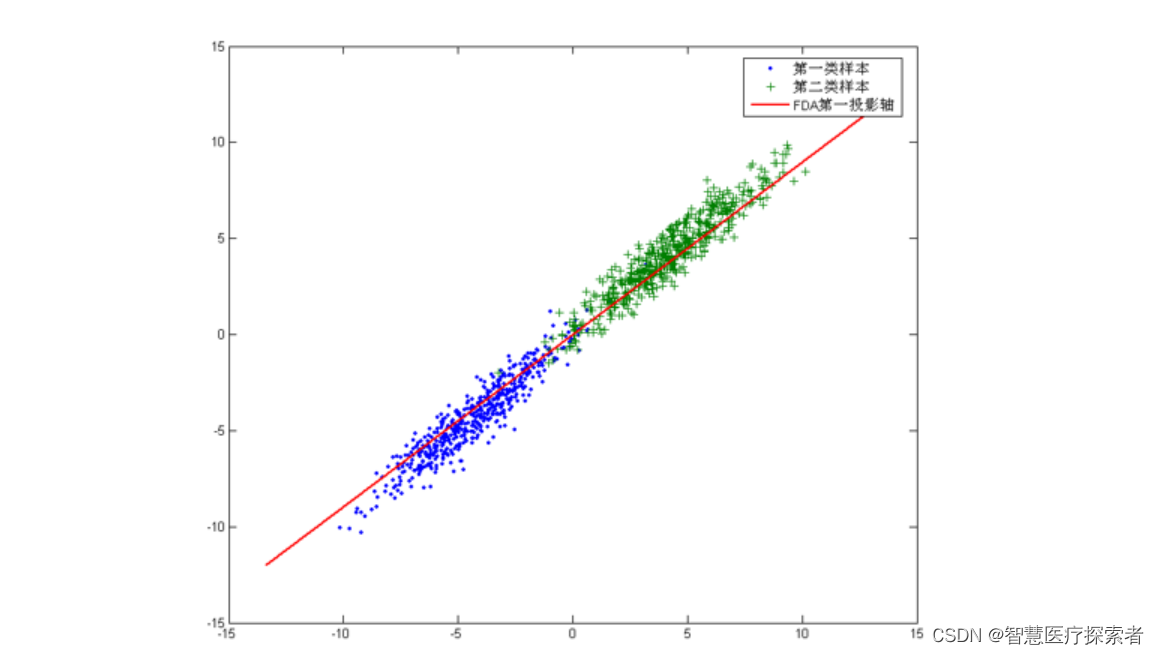
算法详见：https://blog.csdn.net/lsb2002/article/details/131843006

?

5 特征工程的挑战

• 自动化： 尽管有些特征工程步骤可以自动化，但很多任务仍需要专业知识和经验判断。

• 复杂性和计算成本： 特征工程可以非常复杂且耗时，特别是在处理大型数据集时。

• 模型依赖性： 不同的模型可能对特征的需求不同，因此特征工程需要针对特定的模型进行调整。

5 总结

特征工程是构建高效机器学习模型的关键。它包括一系列技术和步骤，旨在通过提取、选择和转换特征来优化模型的输入数据。尽管特征工程是一个复杂且需要大量专业知识的过程，但它对于提高模型性能和准确性至关重要。随着机器学习领域的发展，特征工程的方法和工具也在不断进步，使得这一过程更加高效和自动化。