第八章 假设检验（重难点）

1.原假设H0和备择假设H1，深刻记住概念：

?注意：

H0，是想反对的假设，永远放等号的一方。比如大于，大于等于，小于等于三个符号。

H1，是想支持的一方，总有不等号，大于，小于的符号。

2.假设检验的两类错误：

3.检验假设的重要知识点：

一、下面是一个总体的情况?

前提（都假设总体服从正态分布，或者不服从时n大于等于30情况下近似服从正态分布）

分为三种情况：

1.总体均值的检验根据总体方差未已知和大小样本，分为三种情况（使用Z，Z和t检验）

2.总体比例的检验（z检验）

3.总体方差的检验（卡方检验）

二、下面是两个总体的情况

前提（都假设总体服从正态分布，或者不服从时n大于等于30情况下近似服从正态分布）

分为四种情况：

1.两个总体均值之差的检验（根据总体方差和大小样本变化分三种情况，用Z或t统计量）

2.匹配样本的t检验（一个总体经过前后变化得到两份数据）

3.两个总体比例之差的检验（Z检验）

4.两个总体方差比的检验（F检验）

具体展开如下

?

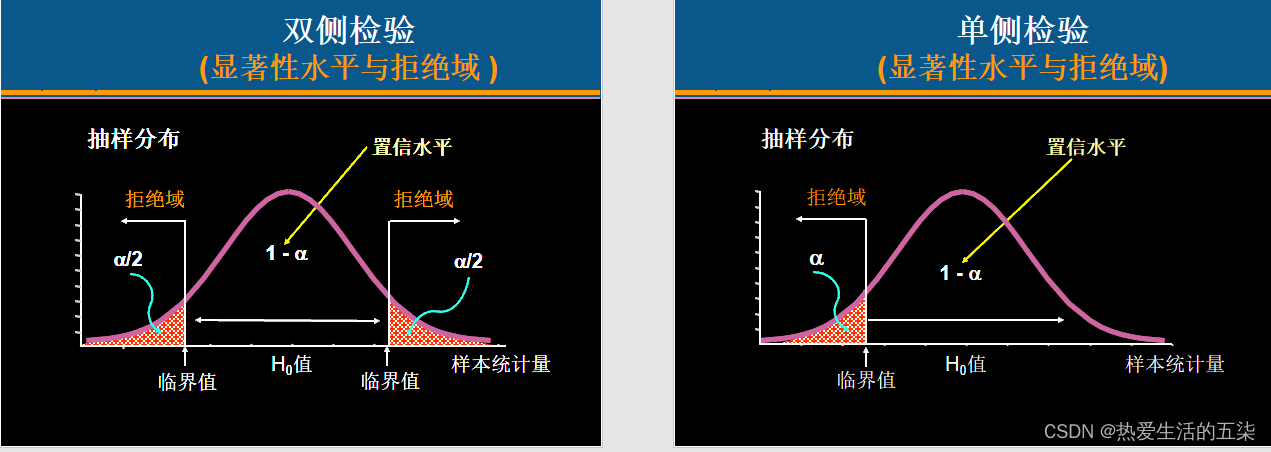
一、下面是一个总体的情况?

前提（都假设总体服从正态分布，或者不服从时n大于等于30情况下近似服从正态分布）

分为三种情况：

1.总体均值的检验根据总体方差未已知和大小样本，分为三种情况（使用Z，Z和t检验）

2.总体比例的检验（z检验）

3.总体方差的检验（卡方检验）

?

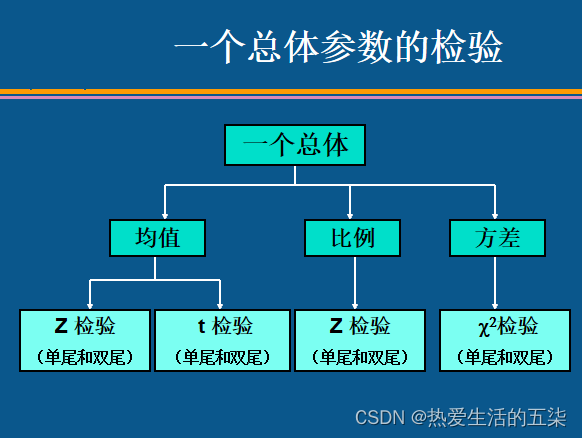
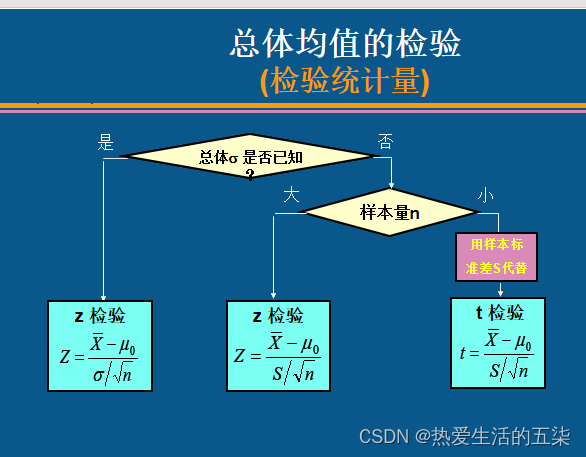
?1.下面是一个总体时总体均值的的检验

?

?

2.一个总体比例的检验：

3.一个总体方差的检验：

二、下面是两个总体的情况

前提（都假设总体服从正态分布，或者不服从时n大于等于30情况下近似服从正态分布）

分为四种情况：

1.两个总体均值之差的检验（根据总体方差和大小样本变化分三种情况，用Z或t统计量）

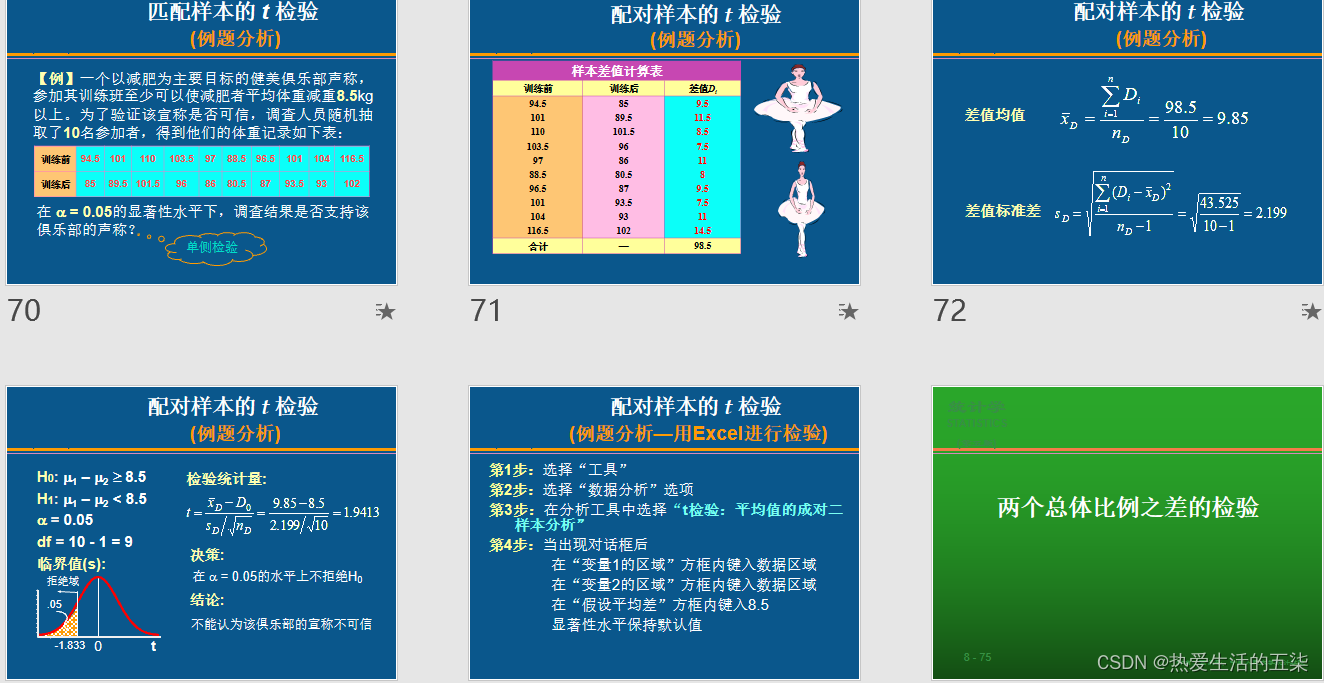
2.匹配样本的t检验（一个总体经过前后变化得到两份数据）

3.两个总体比例之差的检验（Z检验）

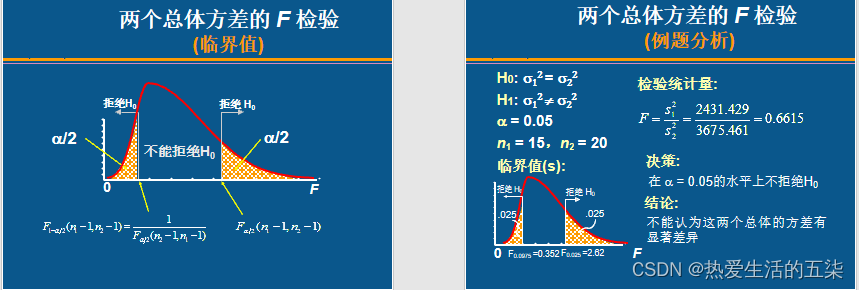
4.两个总体方差比的检验（F检验）

?

?

?

?

?