刷了四百道算法题,我在项目里用过哪几道呢?
大家好,我是老三,今天和大家聊一个话题:项目中用到的力扣算法。
不知道从什么时候起,算法已经成为了互联网面试的标配,在十年前,哪怕如日中天的百度,面试也最多考个冒泡排序。后来,互联网越来越热,涌进来的人越来越多,整个行业越来越内卷的,算法也慢慢成了大小互联网公司面试的标配,力扣现在已经超过3000题了,那么这些题目有多少进入了面试的考察呢?
以最爱考算法的字节跳动为例,看看力扣的企业题库,发现考过的题目已经有1850道——按照平均每道题花20分钟来算,刷完字节题库的算法题需要37000分钟,616.66小时,按每天刷满8小时算,需要77.08天,一周刷五天,需要15.41周,按一个月四周,需要3.85个月。也就是说,在脱产,最理想的状态下,刷完力扣的字节题库,需要差不多4个月时间。

那么,我在项目里用过,包括在项目中见过哪些力扣上的算法呢?我目前刷了400多道题,翻来覆去盘点了一下,发现,也就这么几道。
1.版本比较:比较客户端版本
场景
在日常的开发中,我们很多时候可能面临这样的情况,兼容客户端的版本,尤其是Android和iPhone,有些功能是低版本不支持的,或者说有些功能到了高版本就废弃掉。
这时候就需要进行客户端的版本比较,客户端版本号通常是这种格式6.3.40,这是一个字符串,那就肯定不能用数字类型的比较方法,需要自己定义一个比较的工具方法。

题目
165. 比较版本号
这个场景对应LeetCode: 165. 比较版本号。
-
题目:165. 比较版本号 (https://leetcode.cn/problems/compare-version-numbers/)
-
难度:中等
-
标签:
双指针字符串 -
描述:
给你两个版本号
version1和version2,请你比较它们。版本号由一个或多个修订号组成,各修订号由一个
'.'连接。每个修订号由 多位数字 组成,可能包含 前导零 。每个版本号至少包含一个字符。修订号从左到右编号,下标从 0 开始,最左边的修订号下标为 0 ,下一个修订号下标为 1 ,以此类推。例如,2.5.33和0.1都是有效的版本号。比较版本号时,请按从左到右的顺序依次比较它们的修订号。比较修订号时,只需比较 忽略任何前导零后的整数值 。也就是说,修订号
1和修订号001相等 。如果版本号没有指定某个下标处的修订号,则该修订号视为0。例如,版本1.0小于版本1.1,因为它们下标为0的修订号相同,而下标为1的修订号分别为0和1,0 < 1。返回规则如下:
- 如果
*version1* > *version2*返回1, - 如果
*version1* < *version2*返回-1, - 除此之外返回
0。
示例 1:
输入:version1 = "1.01", version2 = "1.001" 输出:0 解释:忽略前导零,"01" 和 "001" 都表示相同的整数 "1"示例 2:
输入:version1 = "1.0", version2 = "1.0.0" 输出:0 解释:version1 没有指定下标为 2 的修订号,即视为 "0"示例 3:
输入:version1 = "0.1", version2 = "1.1" 输出:-1 解释:version1 中下标为 0 的修订号是 "0",version2 中下标为 0 的修订号是 "1" 。0 < 1,所以 version1 < version2提示:
1 <= version1.length, version2.length <= 500version1和version2仅包含数字和'.'version1和version2都是 有效版本号version1和version2的所有修订号都可以存储在 32 位整数 中
- 如果
解法
那么这道题怎么解呢?这道题其实是一道字符串模拟题,就像标签里给出了了双指针,这道题我们可以用双指针+累加来解决。
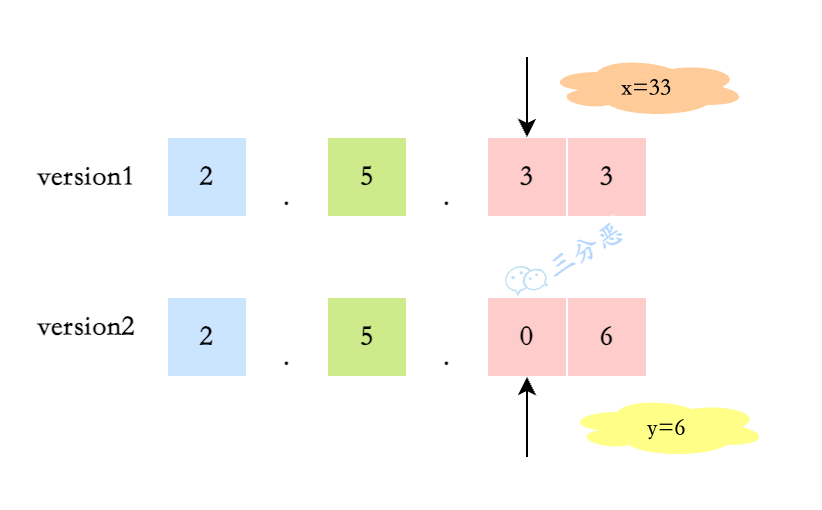
- 两个指针遍历
version1和version2 - 将
.作为分隔符,通过累加获取每个区间代表的数字 - 比较数字的大小,这种方式正好可以忽略前导0
来看看代码:
class Solution {
public int compareVersion(String version1, String version2) {
int m = version1.length();
int n = version2.length();
//两个指针
int p = 0, q = 0;
while (p < m || q < n) {
//累加version1区间的数字
int x = 0;
while (p < m && version1.charAt(p) != '.') {
x += x * 10 + (version1.charAt(p) - '0');
p++;
}
//累加version2区间的数字
int y = 0;
while (q < n && version2.charAt(q) != '.') {
y += y * 10 + (version2.charAt(q) - '0');
q++;
}
//判断
if (x > y) {
return 1;
}
if (x < y) {
return -1;
}
//跳过.
p++;
q++;
}
//version1等于version2
return 0;
}
}
应用
这段代码,直接CV过来,就可以直接当做一个工具类的工具方法来使用:
public class VersionUtil {
public static Integer compareVersion(String version1, String version2) {
int m = version1.length();
int n = version2.length();
//两个指针
int p = 0, q = 0;
while (p < m || q < n) {
//累加version1区间的数字
int x = 0;
while (p < m && version1.charAt(p) != '.') {
x += x * 10 + (version1.charAt(p) - '0');
p++;
}
//累加version2区间的数字
int y = 0;
while (q < n && version2.charAt(q) != '.') {
y += y * 10 + (version2.charAt(q) - '0');
q++;
}
//判断
if (x > y) {
return 1;
}
if (x < y) {
return -1;
}
//跳过.
p++;
q++;
}
//version1等于version2
return 0;
}
}
前面老三分享过一个规则引擎:这款轻量级规则引擎,真香!
比较版本号的方法,还可以结合规则引擎来使用:
-
自定义函数:利用
AviatorScript的自定义函数特性,自定义一个版本比较函数/** * 自定义版本比较函数 */ class VersionFunction extends AbstractFunction { @Override public String getName() { return "compareVersion"; } @Override public AviatorObject call(Map<String, Object> env, AviatorObject arg1, AviatorObject arg2) { // 获取版本 String version1 = FunctionUtils.getStringValue(arg1, env); String version2 = FunctionUtils.getStringValue(arg2, env); return new AviatorBigInt(VersionUtil.compareVersion(version1, version2)); } } -
注册函数:将自定义的函数注册到
AviatorEvaluatorInstance中/** * 注册自定义函数 */ @Bean public AviatorEvaluatorInstance aviatorEvaluatorInstance() { AviatorEvaluatorInstance instance = AviatorEvaluator.getInstance(); // 默认开启缓存 instance.setCachedExpressionByDefault(true); // 使用LRU缓存,最大值为100个。 instance.useLRUExpressionCache(100); // 注册内置函数,版本比较函数。 instance.addFunction(new VersionFunction()); return instance; } -
代码传递上下文:在业务代码里传入客户端、客户端版本的上下文
/** * @param device 设备 * @param version 版本 * @param rule 规则脚本 * @return 是否过滤 */ public boolean filter(String device, String version, String rule) { // 执行参数 Map<String, Object> env = new HashMap<>(); env.put("device", device); env.put("version", version); //编译脚本 Expression expression = aviatorEvaluatorInstance.compile(DigestUtils.md5DigestAsHex(rule.getBytes()), rule, true); //执行脚本 boolean isMatch = (boolean) expression.execute(env); return isMatch; } -
编写脚本:接下来我们就可以编写规则脚本,规则脚本可以放在数据库,也可以放在配置中心,这样就可以灵活改动客户端的版本控制规则
if(device==bil){ return false; } ## 控制Android的版本 if (device=="Android" && compareVersion(version,"1.38.1")<0){ return false; } return true;
2.N叉数层序遍历:翻译商品类型
场景
一个跨境电商网站,现在有这么一个需求:把商品的类型进行国际化翻译。
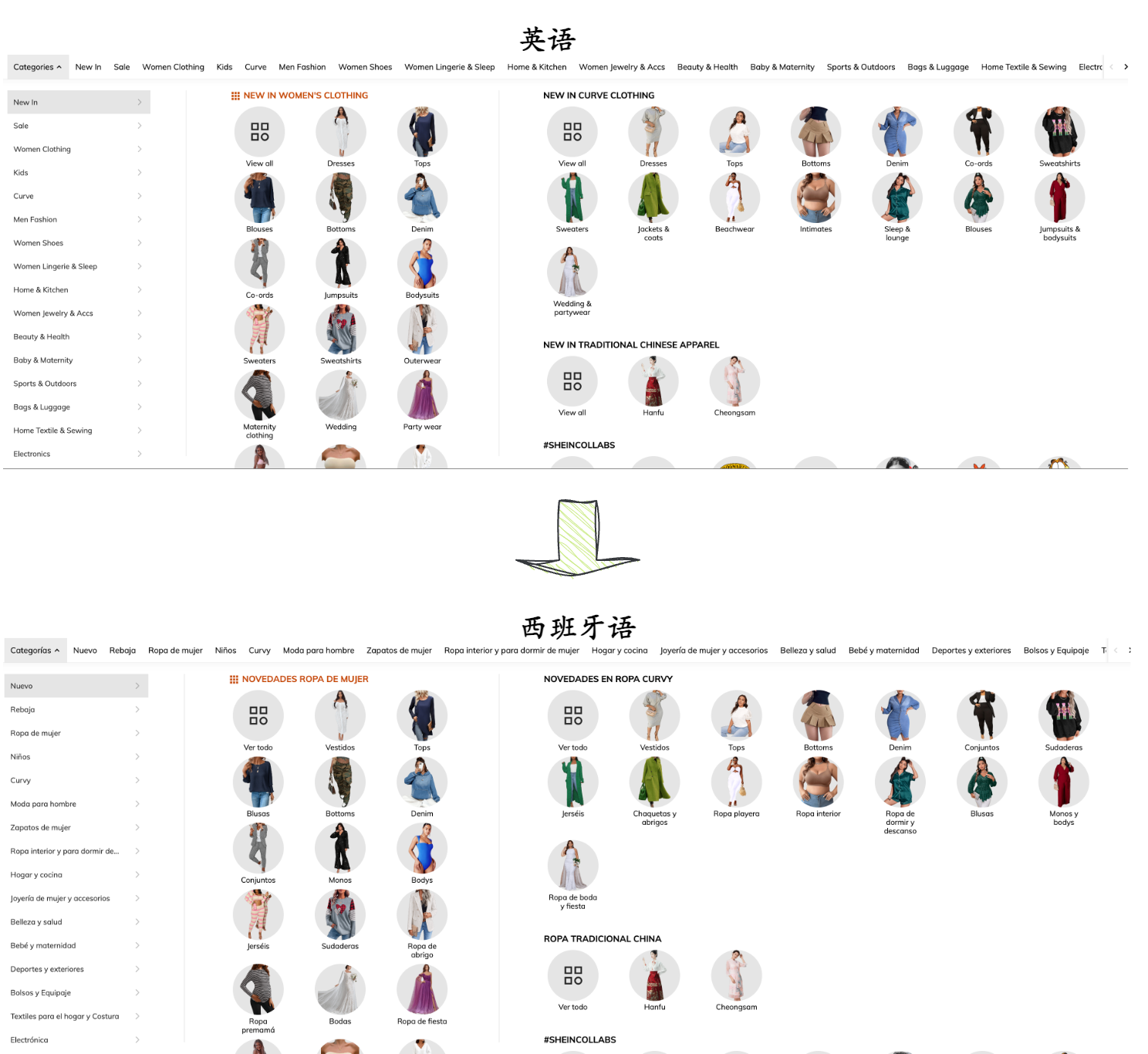
商品的类型是什么结构呢?一级类型下面还有子类型,字类型下面还有子类型,我们把结构一画,发现这就是一个N叉树的结构嘛。
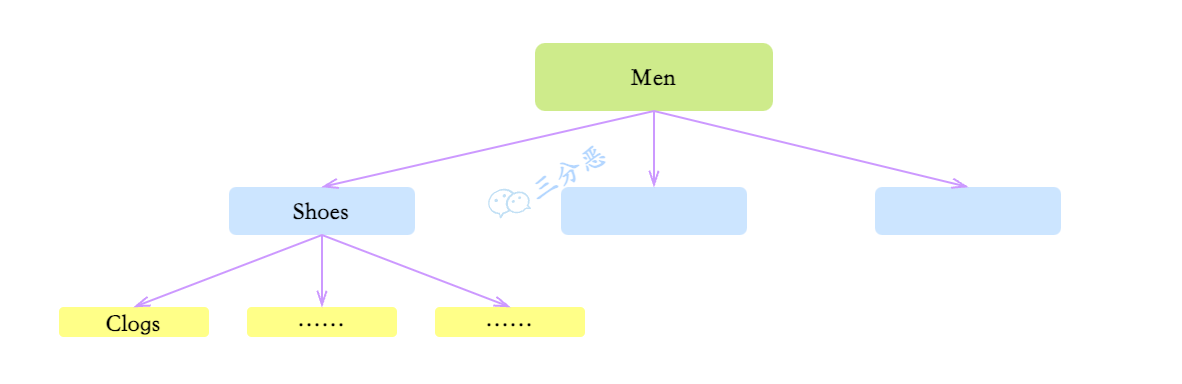
翻译商品类型,要做的事情,就是遍历这棵树,翻译节点上的类型,这不妥妥的BFS或者DFS!
题目
429. N 叉树的层序遍历
这个场景对应LeetCode:429. N 叉树的层序遍历。
-
题目:429. N 叉树的层序遍历(https://leetcode.cn/problems/n-ary-tree-level-order-traversal/)
-
难度:中等
-
标签:
树广度优先搜索 -
描述:
给定一个 N 叉树,返回其节点值的层序遍历。(即从左到右,逐层遍历)。
树的序列化输入是用层序遍历,每组子节点都由 null 值分隔(参见示例)。
示例 1:
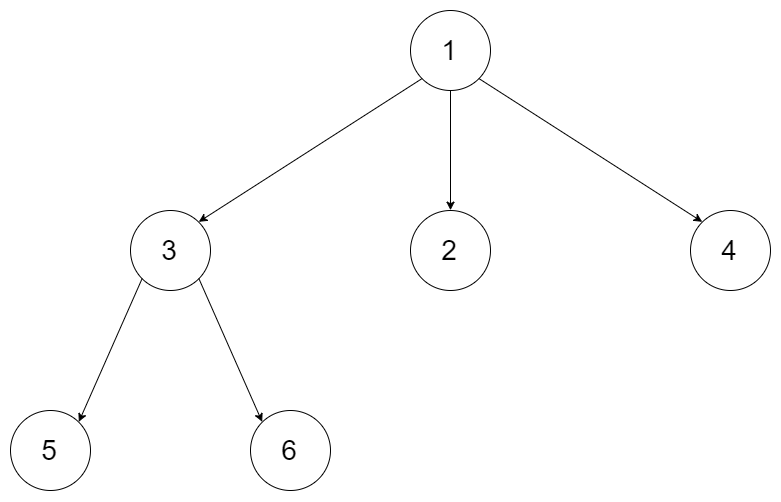
输入:root = [1,null,3,2,4,null,5,6] 输出:[[1],[3,2,4],[5,6]]示例 2:
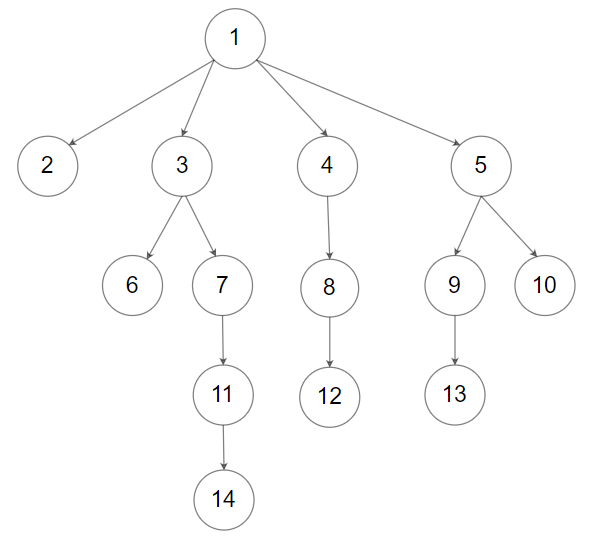
输入:root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14] 输出:[[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]]提示:
- 树的高度不会超过
1000 - 树的节点总数在
[0, 10^4]之间
- 树的高度不会超过
解法
BFS想必很多同学都很熟悉了,DFS的秘诀是栈,BFS的秘诀是队列。
层序遍历的思路是什么呢?
使用队列,把每一层的节点存储进去,一层存储结束之后,我们把队列中的节点再取出来,孩子节点不为空,就把孩子节点放进去队列里,循环往复。
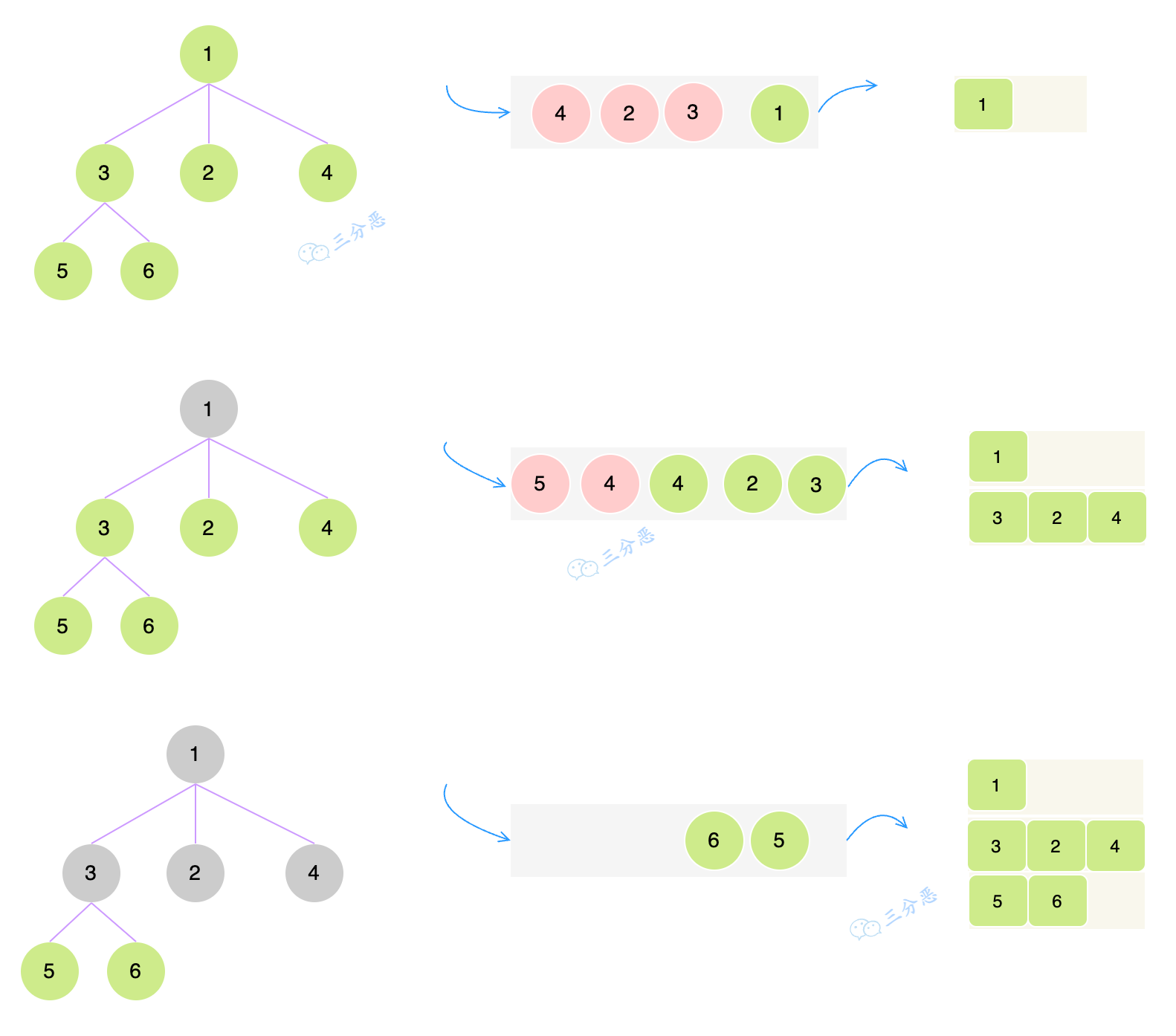
代码如下:
class Solution {
public List<List<Integer>> levelOrder(Node root) {
List<List<Integer>> result = new ArrayList<>();
if (root == null) {
return result;
}
//创建队列并存储根节点
Deque<Node> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
//存储每层结果
List<Integer> level = new ArrayList<>();
int size = queue.size();
for (int i = 0; i < size; i++) {
Node current = queue.poll();
level.add(current.val);
//添加孩子
if (current.children != null) {
for (Node child : current.children) {
queue.offer(child);
}
}
}
//每层遍历结束,添加结果
result.add(level);
}
return result;
}
}
应用
商品类型翻译这个场景下,基本上和这道题目大差不差,不过是两点小区别:
- 商品类型是一个属性多一些的树节点
- 翻译过程直接替换类型名称即可,不需要返回值
来看下代码:
-
ProductCategory:商品分类实体
public class ProductCategory { /** * 分类id */ private String id; /** * 分类名称 */ private String name; /** * 分类描述 */ private String description; /** * 子分类 */ private List<ProductCategory> children; //省略getter、setter } -
translateProductCategory:翻译商品类型方法
public void translateProductCategory(ProductCategory root) { if (root == null) { return; } Deque<ProductCategory> queue = new LinkedList<>(); queue.offer(root); //遍历商品类型,翻译 while (!queue.isEmpty()) { int size = queue.size(); //遍历当前层 for (int i = 0; i < size; i++) { ProductCategory current = queue.poll(); //翻译 String translation = translate(current.getName()); current.setName(translation); //添加孩子 if (current.getChildren() != null && !current.getChildren().isEmpty()) { for (ProductCategory child : current.getChildren()) { queue.offer(child); } } } } }
3.前缀和+二分查找:渠道选择
场景
在电商的交易支付中,我们可以选择一些支付方式,来进行支付,当然,这只是交易的表象。
在支付的背后,一种支付方式,可能会有很多种支付渠道,比如Stripe、Adyen、Alipay,涉及到多个渠道,那么就涉及到决策,用户的这笔交易,到底交给哪个渠道呢?
这其实是个路由问题,答案是加权随机,每个渠道有一定的权重,随机落到某个渠道,加权随机有很多种实现方式,其中一种就是前缀和+二分查找。简单说,就是先累积所有元素权重,再使用二分查找来快速查找。
题目
先来看看对应的LeetCode的题目,这里用到了两个算法:前缀和和二分查找。
704. 二分查找
-
题目:704. 二分查找(https://leetcode.cn/problems/binary-search)
-
难度:简单
-
标签:
数组二分查找 -
描述:
给定一个
n个元素有序的(升序)整型数组nums和一个目标值target,写一个函数搜索nums中的target,如果目标值存在返回下标,否则返回-1。示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9 输出: 4 解释: 9 出现在 nums 中并且下标为 4示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2 输出: -1 解释: 2 不存在 nums 中因此返回 -1提示:
- 你可以假设
nums中的所有元素是不重复的。 n将在[1, 10000]之间。nums的每个元素都将在[-9999, 9999]之间。
- 你可以假设
解法
二分查找可以说我们都很熟了。
数组是有序的,定义三个指针,left、right、mid,其中mid是left、right的中间指针,每次中间指针指向的元素nums[mid]比较和target比较:
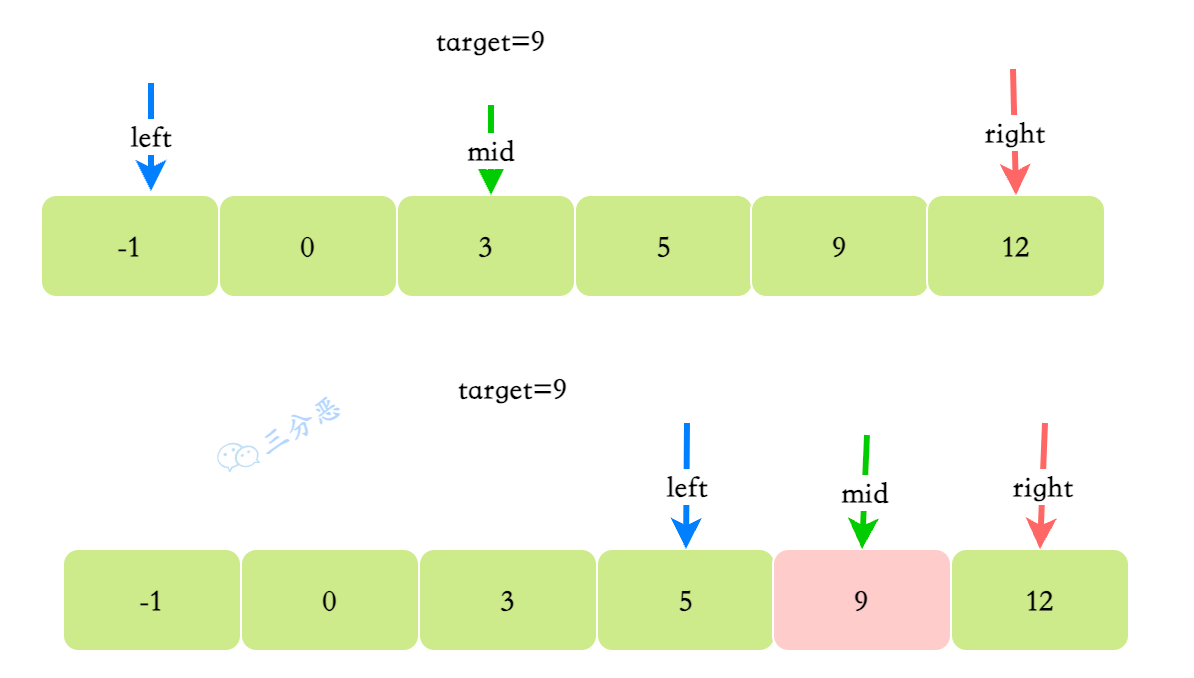
- 如果
nums[mid]等于target,找到目标 - 如果
nums[mid]小于target,目标元素在(mid,right]区间; - 如果
nums[mid]大于target,目标元素在[left,mid)区间
代码:
class Solution {
public int search(int[] nums, int target) {
int left=0;
int right=nums.length-1;
while(left<=right){
int mid=left+((right-left)>>1);
if(nums[mid]==target){
return mid;
}else if(nums[mid]<target){
//target在(mid,right]区间,右移
left=mid+1;
}else{
//target在[left,mid)区间,左移
right=mid-1;
}
}
return -1;
}
}
二分查找,有一个需要注意的细节,计算mid的时候: int mid = left + ((right - left) >> 1);,为什么要这么写呢?
因为这种写法int mid = (left + right) / 2;,可能会因为left和right数值太大导致内存溢出。同时,使用位运算,也是除以2最高效的写法。
——这里有个彩蛋,后面再说。
303. 区域和检索 - 数组不可变
不像二分查找,在LeetCode上,前缀和没有直接的题目,因为本身前缀和更多是一种思路,一种工具,其中303. 区域和检索 - 数组不可变 是一道典型的前缀和题目。
-
题目:303. 区域和检索 - 数组不可变(https://leetcode.cn/problems/range-sum-query-immutable/)
-
难度:简单
-
标签:
设计数组前缀和 -
描述:
给定一个整数数组
nums,处理以下类型的多个查询:- 计算索引
left和right(包含left和right)之间的nums元素的 和 ,其中left <= right
实现
NumArray类:NumArray(int[] nums)使用数组nums初始化对象int sumRange(int i, int j)返回数组nums中索引left和right之间的元素的 总和 ,包含left和right两点(也就是nums[left] + nums[left + 1] + ... + nums[right])
示例 1:
输入: ["NumArray", "sumRange", "sumRange", "sumRange"] [[[-2, 0, 3, -5, 2, -1]], [0, 2], [2, 5], [0, 5]] 输出: [null, 1, -1, -3] 解释: NumArray numArray = new NumArray([-2, 0, 3, -5, 2, -1]); numArray.sumRange(0, 2); // return 1 ((-2) + 0 + 3) numArray.sumRange(2, 5); // return -1 (3 + (-5) + 2 + (-1)) numArray.sumRange(0, 5); // return -3 ((-2) + 0 + 3 + (-5) + 2 + (-1))提示:
1 <= nums.length <= 104-105 <= nums[i] <= 1050 <= i <= j < nums.length- 最多调用
104次sumRange方法
- 计算索引
解法
这道题,我们如果不用前缀和的话,写起来也很简单:
class NumArray {
private int[] nums;
public NumArray(int[] nums) {
this.nums=nums;
}
public int sumRange(int left, int right) {
int res=0;
for(int i=left;i<=right;i++){
res+=nums[i];
}
return res;
}
}
当然时间复杂度偏高,O(n),那么怎么使用前缀和呢?
- 构建一个前缀和数组,用来累积
(0……i-1)的和,这样一来,我们就可以直接计算[left,right]之间的累加和
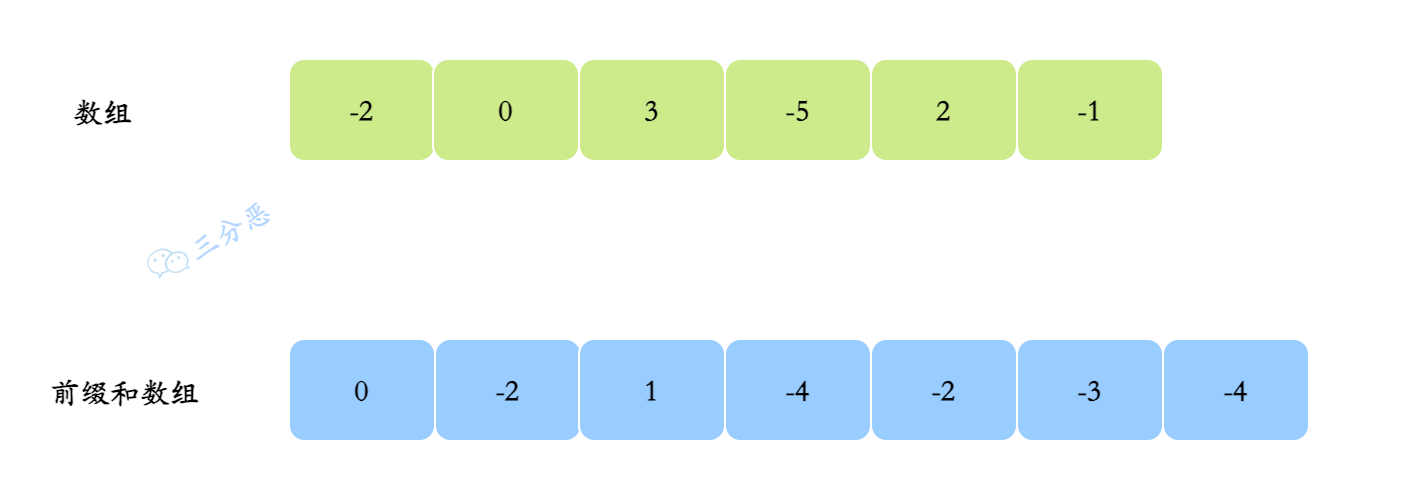
代码如下:
class NumArray {
private int[] preSum;
public NumArray(int[] nums) {
int n=nums.length;
preSum=new int[n+1];
//计算nums的前缀和
for(int i=0;i<n;i++){
preSum[i+1]=preSum[i]+nums[i];
}
}
//直接算出区间[left,right]的累加和
public int sumRange(int left, int right) {
return preSum[right+1]-preSum[left];
}
}
可以看到,通过前缀和数组,可以直接算出区间[left,right]的累加和,时间复杂度O(1),可以说非常高效了。
应用
了解了前缀和和二分查找之后,回归我们之前的场景,使用前缀和+二分查找来实现加权随机,从而实现对渠道的分流选择。
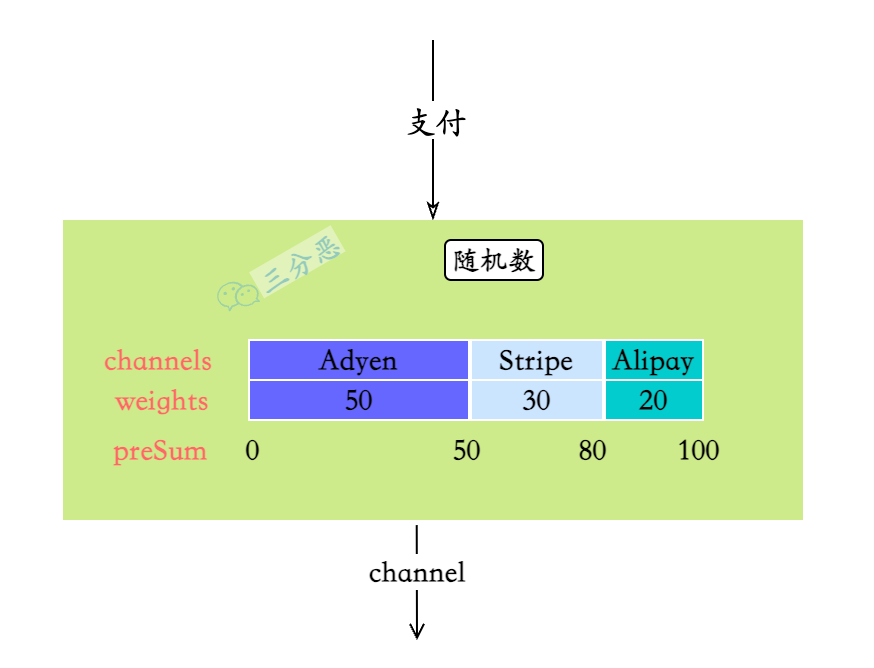
- 需要根据渠道和权重的配置,生成一个前缀和数组,来累积权重的值,渠道也通过一个数组进行分配映射
- 用户的支付请求进来的时候,生成一个随机数,二分查找找到随机数载前缀和数组的位置,映射到渠道数组
- 最后通过渠道数组的映射,找到选中的渠道
代码如下:
/**
* 支付渠道分配器
*/
public class PaymentChannelAllocator {
//渠道数组
private String[] channels;
//前缀和数组
private int[] preSum;
private ThreadLocalRandom random;
/**
* 构造方法
*
* @param channelWeights 渠道分流权重
*/
public PaymentChannelAllocator(HashMap<String, Integer> channelWeights) {
this.random = ThreadLocalRandom.current();
// 初始化channels和preSum数组
channels = new String[channelWeights.size()];
preSum = new int[channelWeights.size()];
// 计算前缀和
int index = 0;
int sum = 0;
for (String channel : channelWeights.keySet()) {
sum += channelWeights.get(channel);
channels[index] = channel;
preSum[index++] = sum;
}
}
/**
* 渠道选择
*/
public String allocate() {
// 生成一个随机数
int rand = random.nextInt(preSum[preSum.length - 1]) + 1;
// 通过二分查找在前缀和数组查找随机数所在的区间
int channelIndex = binarySearch(preSum, rand);
return channels[channelIndex];
}
/**
* 二分查找
*/
private int binarySearch(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
while (left <= right) {
int mid = left + ((right - left) >> 2);
if (nums[mid] == target) {
return mid;
} else if (nums[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
// 当找不到确切匹配时返回大于随机数的最小前缀和的索引
return left;
}
}
测试一下:
@Test
void allocate() {
HashMap<String, Integer> channels = new HashMap<>();
channels.put("Adyen", 50);
channels.put("Stripe", 30);
channels.put("Alipay", 20);
PaymentChannelAllocator allocator = new PaymentChannelAllocator(channels);
// 模拟100次交易分配
for (int i = 0; i < 100; i++) {
String allocatedChannel = allocator.allocate();
System.out.println("Transaction " + (i + 1) + " allocated to: " + allocatedChannel);
}
}
彩蛋
在这个渠道选择的场景里,还有两个小彩蛋。
二分查找翻车
我前面提到了一个二分查找求mid的写法:
int mid=left+((right-left)>>1);
这个写法机能防止内存溢出,用了位移运算也很高效,但是,这个简单的二分查找写出过问题,直接导致线上cpu飙升,差点给老三吓尿了。

int mid = (right - left) >> 2 + left;
就是这行代码,看出什么问题来了吗?
——它会导致循环结束不了!
为什么呢?因为>>运算的优先级是要低于+的,所以这个运算实际上等于:
int mid = (right - left) >> (2 + left);
在只有两个渠道的时候没有问题,三个的时候就寄了。
当然,最主要原因还是没有充分测试,所以大家知道我在上面为什么特意写了单测吧。
加权随机其它写法
这里用了前缀和+二分查找来实现加权随机,其实加权随机还有一些其它的实现方法,包括别名方法、树状数组、线段树**、随机列表扩展、**权重累积等等方法,大家感兴趣可以了解一下。
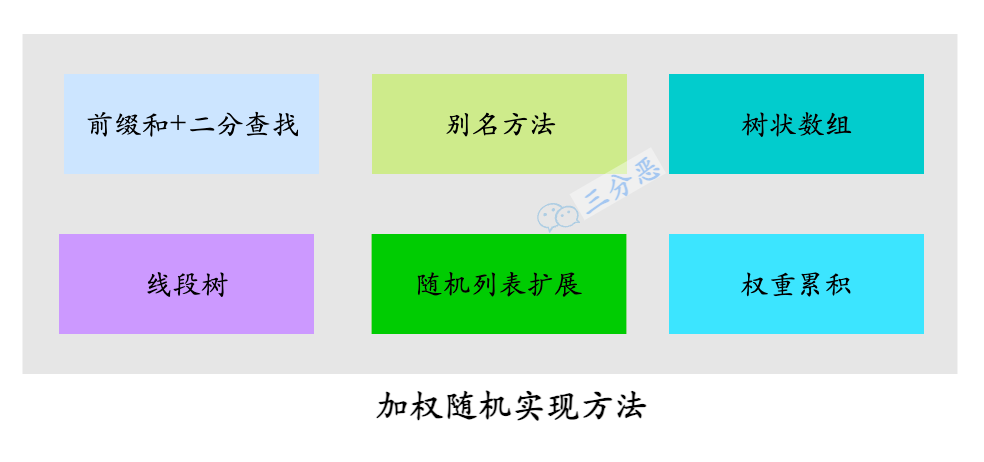
印象比较深刻的是,有场面试被问到了怎么实现加权随机,我回答了权重累积、前缀和+二分查找,面试官还是不太满意,最后面试官给出了他的答案——随机列表扩展。
什么是随机列表扩展呢?简单说,就是创建一个足够大的列表,根据权重,在相应的区间,放入对应的渠道,生成随机数的时候,就可以直接获取对应位置的渠道。
public class WeightedRandomList {
private final List<String> expandedList = new ArrayList<>();
private final Random random = new Random();
public WeightedRandomList(HashMap<String, Integer> weightMap) {
// 填充 expandedList,根据权重重复元素
for (String item : weightMap.keySet()) {
int weight = weightMap.get(item);
for (int i = 0; i < weight; i++) {
expandedList.add(item);
}
}
}
public String getRandomItem() {
// 生成随机索引并返回对应元素
int index = random.nextInt(expandedList.size());
return expandedList.get(index);
}
public static void main(String[] args) {
HashMap<String, Integer> items = new HashMap<>();
items.put("Alipay", 60);
items.put("Adyen", 20);
items.put("Stripe", 10);
WeightedRandomList wrl = new WeightedRandomList(items);
// 演示随机选择
for (int i = 0; i < 10; i++) {
System.out.println(wrl.getRandomItem());
}
}
}
这种实现方式就是典型的空间换时间,空间复杂度O(n),时间复杂度O(1)。优点是时间复杂度低,缺点是空间复杂度高,如果权重总和特别大的时候,就需要一个特别大的列表来存储元素。
当然这种写法还是很巧妙的,适合元素少、权重总和小的场景。
刷题随想
上面就是我在项目里用到过或者见到过的LeetCode算法应用,416:4,不足1%的使用率,还搞出过严重的线上问题。
……
在力扣社区里关于算法有什么的贴子里,有这样的回复:
“最好的结构是数组,最好的算法是遍历”。
“最好的算法思路是暴力。”
……
坦白说,如果不是为了面试,我是绝对不会去刷算法的,上百个小时,用在其他地方,绝对收益会高很多。
从实际应用去找刷LeetCode算法的意义,本身没有太大意义,算法题的最大意义就是面试。
刷了能过,不刷就挂,仅此而已。
这些年互联网行业红利消失,越来越多的算法题,只是内卷的产物而已。
当然,从另外一个角度来看,考察算法,对于普通的打工人,可能是个更公平的方式——学历、背景都很难卷出来,但是算法可以。
我去年面试的真实感受,“没机会”比“面试难”更令人绝望。
写到这,有点难受,刷几道题缓一下!
参考:
[1].https://leetcode.cn/circle/discuss/29Y1td/
[2].https://36kr.com/p/1212436260343689
[3].https://leetcode.cn/circle/discuss/QXnn1F/
[4].https://leetcode.cn/circle/discuss/SrePlc/
备注:涉及敏感信息,文中的代码都不是真实的投产代码,作者进行了一定的脱敏和演绎。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!