pl_vio线特征

0.引言

• PL-VIO，本文关注线段。
• 论文链接

1.LineFeatureTracker核心逻辑解读

• 数据结构定义：

struct Line {
  Point2f StartPt;
  Point2f EndPt;
  float lineWidth;
  Point2f Vp;

  Point2f Center;
  Point2f unitDir;  // [cos(theta), sin(theta)]
  float length;
  float theta;

  // para_a * x + para_b * y + c = 0
  float para_a;
  float para_b;
  float para_c;

  float image_dx;
  float image_dy;
  float line_grad_avg;

  float xMin;
  float xMax;
  float yMin;
  float yMax;
  unsigned short id;
  int colorIdx;
};

class FrameLines {
 public:
  int frame_id;
  Mat img;

  vector<Line> vecLine;
  vector<int> lineID;

  // opencv3 lsd+lbd
  std::vector<KeyLine> keylsd;
  Mat lbd_descr;
};

• keylsd：提取的线段结果（经过长度筛选的，太短的不要）
• keylbd_descr：对应线段描述子结果（经过长度筛选的，太短的不要）
• 新进的img提取线特征：
  • 如果是第一帧img：forwframe_->lineID.push_back(allfeature_cnt++)；（allfeature_cnt是整个系统全局的线特征计数）,因此lineID是全局的ID，整个系统中线特征具有唯一的ID。update:后面更新的是没匹配上的。
  • 如果不是第一帧img，则暂时赋值为-1，但forwframe_->lineID数组的size的大小是和keylsd相同的；
    • 匹配后将-1进行更改：forwframe_->lineID[mt.queryIdx] = curframe_->lineID[mt.trainIdx];
      • Key = 当前帧线段的ID
      • Value = 前一帧线段的lineID[mt.trainIdx]
    • 判断当前帧水平，垂直方向线段数量是否分别足够35条，不够的补上。

匹配的结果，对应关系，其实就是存储的全局ID信息。

代码注释，可惜另一个函数的关键内容lineDetector没放出来，这个函数的vecLine只在最后做了一个转换。frame_id没维护。

void LineFeatureTracker::readImage(const cv::Mat &_img) {
  cv::Mat img;
  TicToc t_p;
  frame_cnt++;

  //   cv::remap(_img, img, undist_map1_, undist_map2_, CV_INTER_LINEAR);
  cv::remap(_img, img, undist_map1_, undist_map2_, cv::INTER_LINEAR);
  //    cv::imshow("lineimg",img);
  //    cv::waitKey(1);
  // ROS_INFO("undistortImage costs: %fms", t_p.toc());
  if (EQUALIZE)  // 直方图均衡化
  {
    cv::Ptr<cv::CLAHE> clahe = cv::createCLAHE(3.0, cv::Size(8, 8));
    clahe->apply(img, img);
  }

  bool first_img = false;
  if (forwframe_ == nullptr)  // 系统初始化的第一帧图像
  {
    forwframe_.reset(new FrameLines);
    curframe_.reset(new FrameLines);
    forwframe_->img = img;
    curframe_->img = img;  // 上一帧
    first_img = true;
  } else {
    forwframe_.reset(new FrameLines);  // 初始化一个新的帧
    forwframe_->img = img;             // 当前帧
  }
  TicToc t_li;
  Ptr<line_descriptor::LSDDetectorC> lsd_ =
      line_descriptor::LSDDetectorC::createLSDDetectorC();
  // lsd parameters
  line_descriptor::LSDDetectorC::LSDOptions opts;
  opts.refine = 1;   // 1     	The way found lines will be refined
  opts.scale = 0.5;  // 0.8   	The scale of the image that will be used to find
                     // the lines. Range (0..1].
  opts.sigma_scale = 0.6;  // 0.6  	Sigma for Gaussian filter. It is
                           // computed as sigma = _sigma_scale/_scale.
  opts.quant =
      2.0;  // 2.0   Bound to the quantization error on the gradient norm
  opts.ang_th = 22.5;  // 22.5	Gradient angle tolerance in degrees
  opts.log_eps = 1.0;  // 0		Detection threshold: -log10(NFA) >
                       // log_eps. Used only when advance refinement is chosen
  opts.density_th = 0.6;  // 0.7	Minimal density of aligned region points
                          // in the enclosing rectangle.
  opts.n_bins =
      1024;  // 1024 	Number of bins in pseudo-ordering of gradient modulus.
  double min_line_length =
      0.125;  // Line segments shorter than that are rejected
  // opts.refine       = 1;
  // opts.scale        = 0.5;
  // opts.sigma_scale  = 0.6;
  // opts.quant        = 2.0;
  // opts.ang_th       = 22.5;
  // opts.log_eps      = 1.0;
  // opts.density_th   = 0.6;
  // opts.n_bins       = 1024;
  // double min_line_length = 0.125;
  opts.min_length = min_line_length * (std::min(img.cols, img.rows));

  std::vector<KeyLine> lsd, keylsd;
  // void LSDDetectorC::detect( const std::vector<Mat>& images,
  // std::vector<std::vector<KeyLine> >& keylines, int scale, int numOctaves,
  // const std::vector<Mat>& masks ) const
  lsd_->detect(img, lsd, 2, 1, opts);
  // visualize_line(img,lsd);
  // step 1: line extraction
  // TicToc t_li;
  // std::vector<KeyLine> lsd, keylsd;
  // Ptr<LSDDetector> lsd_;
  // lsd_ = cv::line_descriptor::LSDDetector::createLSDDetector();
  // lsd_->detect( img, lsd, 2, 2 );

  sum_time += t_li.toc();
  ROS_INFO("line detect costs: %fms", t_li.toc());

  Mat lbd_descr, keylbd_descr;
  // step 2: lbd descriptor
  TicToc t_lbd;
  Ptr<BinaryDescriptor> bd_ = BinaryDescriptor::createBinaryDescriptor();

  bd_->compute(img, lsd, lbd_descr);
  // std::cout<<"lbd_descr = "<<lbd_descr.size()<<std::endl;
  //
  for (int i = 0; i < (int)lsd.size(); i++) {
    if (lsd[i].octave == 0 && lsd[i].lineLength >= 60) {  // 对长度做一个筛选
      keylsd.push_back(lsd[i]);
      keylbd_descr.push_back(lbd_descr.row(i));
    }
  }
  // std::cout<<"lbd_descr = "<<lbd_descr.size()<<std::endl;
  //    ROS_INFO("lbd_descr detect costs: %fms", keylsd.size() * t_lbd.toc() /
  //    lsd.size() );
  sum_time += keylsd.size() * t_lbd.toc() / lsd.size();
  ///

  forwframe_->keylsd = keylsd;  // 当前帧的关键线段
  forwframe_->lbd_descr = keylbd_descr;

  for (size_t i = 0; i < forwframe_->keylsd.size(); ++i) {
    if (first_img)
      forwframe_->lineID.push_back(allfeature_cnt++);
    else
      forwframe_->lineID.push_back(-1);  // give a negative id
  }

  // if(!first_img)
  // {
  //     std::vector<DMatch> lsd_matches;
  //     Ptr<BinaryDescriptorMatcher> bdm_;
  //     bdm_ = BinaryDescriptorMatcher::createBinaryDescriptorMatcher();
  //     bdm_->match(forwframe_->lbd_descr, curframe_->lbd_descr, lsd_matches);
  //     visualize_line_match(forwframe_->img.clone(), curframe_->img.clone(),
  //     forwframe_->keylsd, curframe_->keylsd, lsd_matches);
  //     // std::cout<<"lsd_matches = "<<lsd_matches.size()<<"
  //     forwframe_->keylsd = "<<keylbd_descr.size()<<" curframe_->keylsd =
  //     "<<keylbd_descr.size()<<std::endl;
  // }

  if (curframe_->keylsd.size() > 0) {
    /* compute matches */
    TicToc t_match;
    std::vector<DMatch> lsd_matches;
    Ptr<BinaryDescriptorMatcher> bdm_;
    bdm_ = BinaryDescriptorMatcher::createBinaryDescriptorMatcher();
    // 上一帧与当前帧进行匹配
    bdm_->match(forwframe_->lbd_descr, curframe_->lbd_descr, lsd_matches);
    //        ROS_INFO("lbd_macht costs: %fms", t_match.toc());
    sum_time += t_match.toc();
    mean_time = sum_time / frame_cnt;
    // ROS_INFO("line feature tracker mean costs: %fms", mean_time);
    /* select best matches */
    std::vector<DMatch> good_matches;
    std::vector<KeyLine> good_Keylines;
    good_matches.clear();
    for (int i = 0; i < (int)lsd_matches.size(); i++) {
      if (lsd_matches[i].distance < 30) {  // 距离小于30的匹配，认为是好的匹配
        DMatch mt = lsd_matches[i];
        KeyLine line1 = forwframe_->keylsd[mt.queryIdx];
        KeyLine line2 = curframe_->keylsd[mt.trainIdx];
        Point2f serr =
            line1.getStartPoint() - line2.getEndPoint();  // start error
        Point2f eerr = line1.getEndPoint() - line2.getEndPoint();  // end error
        // std::cout<<"11111111111111111 =
        // "<<abs(line1.angle-line2.angle)<<std::endl;
        // 线段在图像里不会跑得特别远,距离和角度的筛选
        if ((serr.dot(serr) < 200 * 200) && (eerr.dot(eerr) < 200 * 200) &&
            abs(line1.angle - line2.angle) < 0.1)
          good_matches.push_back(
              lsd_matches[i]);  // 一个元素存储的是一对匹配关系
      }
    }

    vector<int> success_id;
    // std::cout << forwframe_->lineID.size() <<" " <<curframe_->lineID.size();
    for (int k = 0; k < good_matches.size(); ++k) {
      DMatch mt = good_matches[k];
      //   forwframe_->lineID[mt.queryIdx]
      forwframe_->lineID[mt.queryIdx] = curframe_->lineID[mt.trainIdx];
      success_id.push_back(curframe_->lineID[mt.trainIdx]);
    }

    // visualize_line_match(forwframe_->img.clone(), curframe_->img.clone(),
    // forwframe_->keylsd, curframe_->keylsd, good_matches);

    // 把没追踪到的线存起来
    vector<KeyLine> vecLine_tracked, vecLine_new;
    vector<int> lineID_tracked, lineID_new;
    Mat DEscr_tracked, Descr_new;
    // 将跟踪的线和没跟踪上的线进行区分
    // vecLine_new、lineID_new、 Descr_new当前帧和上一帧没匹配失败的线段信息
    for (size_t i = 0; i < forwframe_->keylsd.size(); ++i) {
      if (forwframe_->lineID[i] == -1) {
        forwframe_->lineID[i] = allfeature_cnt++;
        vecLine_new.push_back(forwframe_->keylsd[i]);
        lineID_new.push_back(forwframe_->lineID[i]);
        Descr_new.push_back(forwframe_->lbd_descr.row(i));
      }

      else {  // vecLine_tracked、lineID_tracked、
              // DEscr_tracked当前帧和上一帧匹配成功的线段信息
        vecLine_tracked.push_back(forwframe_->keylsd[i]);
        lineID_tracked.push_back(forwframe_->lineID[i]);
        DEscr_tracked.push_back(forwframe_->lbd_descr.row(i));
      }
    }

    vector<KeyLine> h_Line_new, v_Line_new;
    vector<int> h_lineID_new, v_lineID_new;
    Mat h_Descr_new, v_Descr_new;
    // 遍历匹配失败的线段，将水平线（horizontal line）和垂直（vertical
    // line）线分开
    for (size_t i = 0; i < vecLine_new.size(); ++i) {
      // 将角度在45度到135度或者-45度到-135度之间的线认为是水平线，其他的线认为是垂直线。是不是反了？
      if ((((vecLine_new[i].angle >= 3.14 / 4 &&
             vecLine_new[i].angle <= 3 * 3.14 / 4)) ||
           (vecLine_new[i].angle <= -3.14 / 4 &&
            vecLine_new[i].angle >= -3 * 3.14 / 4))) {
        h_Line_new.push_back(vecLine_new[i]);
        h_lineID_new.push_back(lineID_new[i]);
        h_Descr_new.push_back(Descr_new.row(i));
      } else {
        v_Line_new.push_back(vecLine_new[i]);
        v_lineID_new.push_back(lineID_new[i]);
        v_Descr_new.push_back(Descr_new.row(i));
      }
    }
    int h_line, v_line;
    h_line = v_line = 0;
    // 遍历匹配成功的线段，统计水平线（horizontal line）和垂直（vertical
    // line）线个数
    for (size_t i = 0; i < vecLine_tracked.size(); ++i) {
      if ((((vecLine_tracked[i].angle >= 3.14 / 4 &&
             vecLine_tracked[i].angle <= 3 * 3.14 / 4)) ||
           (vecLine_tracked[i].angle <= -3.14 / 4 &&
            vecLine_tracked[i].angle >= -3 * 3.14 / 4))) {
        h_line++;
      } else {
        v_line++;
      }
    }
    // 计算匹配成功的线段中水平线（horizontal line）和垂直（vertical
    // line）线的个数是否分别足够35个，不够的话就补充
    int diff_h = 35 - h_line;
    int diff_v = 35 - v_line;

    // std::cout<<"h_line = "<<h_line<<" v_line = "<<v_line<<std::endl;
    // 补充水平线线条
    if (diff_h > 0) {
      int kkk = 1;
      if (diff_h > h_Line_new.size())
        diff_h = h_Line_new.size();
      else
        kkk = int(h_Line_new.size() / diff_h);
      // 作者原本估计是想随机性一点的选择，但是没实现
      for (int k = 0; k < diff_h; ++k) {
        vecLine_tracked.push_back(h_Line_new[k]);
        lineID_tracked.push_back(h_lineID_new[k]);
        DEscr_tracked.push_back(h_Descr_new.row(k));
      }
      // std::cout  <<"h_kkk = " <<kkk<<" diff_h = "<<diff_h<<"
      // h_Line_new.size() = "<<h_Line_new.size()<<std::endl;
    }
    // 补充垂直线条
    if (diff_v > 0) {
      int kkk = 1;
      if (diff_v > v_Line_new.size())
        diff_v = v_Line_new.size();
      else
        kkk = int(v_Line_new.size() / diff_v);
      for (int k = 0; k < diff_v; ++k) {
        vecLine_tracked.push_back(v_Line_new[k]);
        lineID_tracked.push_back(v_lineID_new[k]);
        DEscr_tracked.push_back(v_Descr_new.row(k));
      }  // std::cout  <<"v_kkk = " <<kkk<<" diff_v = "<<diff_v<<"
         // v_Line_new.size() = "<<v_Line_new.size()<<std::endl;
    }
    // int diff_n = 50 - vecLine_tracked.size();  //
    // 跟踪的线特征少于50了，那就补充新的线特征, 还差多少条线 if( diff_n > 0) //
    // 补充线条
    // {
    //     for (int k = 0; k < vecLine_new.size(); ++k) {
    //         vecLine_tracked.push_back(vecLine_new[k]);
    //         lineID_tracked.push_back(lineID_new[k]);
    //         DEscr_tracked.push_back(Descr_new.row(k));
    //     }
    // }

    forwframe_->keylsd = vecLine_tracked;
    forwframe_->lineID = lineID_tracked;
    forwframe_->lbd_descr = DEscr_tracked;
  }

  // 将opencv的KeyLine数据转为季哥的Line
  for (int j = 0; j < forwframe_->keylsd.size(); ++j) {
    Line l;
    KeyLine lsd = forwframe_->keylsd[j];
    l.StartPt = lsd.getStartPoint();
    l.EndPt = lsd.getEndPoint();
    l.length = lsd.lineLength;
    forwframe_->vecLine.push_back(l);
  }
  curframe_ = forwframe_;
}

最后forwframe_->vecLine属性，赋值了三个

l.StartPt = lsd.getStartPoint();
l.EndPt = lsd.getEndPoint();
l.length = lsd.lineLength;

ROS发布的信息

• feature_lines->points ： 线段起点
• feature_lines->channels.push_back(id_of_line); ：与上一帧的匹配关系
• feature_lines->channels.push_back(u_of_endpoint);：线段终点 u 坐标
• feature_lines->channels.push_back(v_of_endpoint);：线段终点 v 坐标

在ROS中，sensor_msgs::PointCloud是一个用于表示3D点云的消息类型。它的数据结构如下：

• std_msgs/Header header：消息头，包含时间戳和坐标帧信息。
• geometry_msgs/Point32[] points：点云中的点，每个点包含x、y和z坐标。
• std_msgs/ChannelFloat32[] channels：每个通道包含一个名字和一组与点对应的浮点数。这可以用来存储与每个点相关的额外数据，如颜色、强度等，这里存储的信息如上所述。

2.estimator_node中线段的处理

2.1.订阅信息解压

map<int, vector<pair<int, Vector4d>>> lines;
for (unsigned int i = 0; i < line_msg->points.size(); i++) {
  int v = line_msg->channels[0].values[i] + 0.5;
  // std::cout<< "receive id: " << v / NUM_OF_CAM << "\n";
  int feature_id = v / NUM_OF_CAM;
  int camera_id =
      v % NUM_OF_CAM;  // 被几号相机观测到的，如果是单目，camera_id = 0
  double x_startpoint = line_msg->points[i].x;
  double y_startpoint = line_msg->points[i].y;
  double x_endpoint = line_msg->channels[1].values[i];
  double y_endpoint = line_msg->channels[2].values[i];
  //                ROS_ASSERT(z == 1);
  lines[feature_id].emplace_back(
      camera_id,
      Vector4d(x_startpoint, y_startpoint, x_endpoint, y_endpoint));
}

map<int, vector<pair<int, Vector4d>>> lines; 其实这里的vetor大小始终是1

• key : 与上一帧线特征的对应关系
• value : camera_id + 线段起点 + 线段终点

2.2.线特征管理

现根据之前匹配的对应关系构造出lineFeaturePerId信息：

// 根据frame进行维护，这里是最初读取的数据
class lineFeaturePerFrame {
 public:
  lineFeaturePerFrame(const Vector4d &line) { lineobs = line; }
  lineFeaturePerFrame(const Vector8d &line) {
    lineobs = line.head<4>();
    lineobs_R = line.tail<4>();
  }
  Vector4d lineobs;  // 每一帧上的观测
  Vector4d lineobs_R;
  double z;
  bool is_used;
  double parallax;
  MatrixXd A;
  VectorXd b;
  double dep_gradient;
};

// 根据id进行维护，该id的线段可能被多帧观测到
class lineFeaturePerId {
 public:
  const int feature_id;   //线特征的全局ID,全局唯一
  int start_frame;

  //  linefeature_per_frame 是个向量容器，存着这个特征在每一帧上的观测量。
  //                    如：feature_per_frame[0]，存的是ft在start_frame上的观测值;
  //                    feature_per_frame[1]存的是start_frame+1上的观测
  // 同一id在不同帧上的观测，统一放到一起，后续会进行三角化
  vector<lineFeaturePerFrame> linefeature_per_frame;

  int used_num;
  bool is_outlier;
  bool is_margin;
  bool is_triangulation;
  Vector6d line_plucker;

  Vector4d obs_init;
  Vector4d obs_j;
  Vector6d line_plk_init;  // used to debug
  Vector3d ptw1;           // used to debug
  Vector3d ptw2;           // used to debug
  Eigen::Vector3d tj_;     // tij
  Eigen::Matrix3d Rj_;
  Eigen::Vector3d ti_;  // tij
  Eigen::Matrix3d Ri_;
  int removed_cnt;
  int all_obs_cnt;   // 这个id的线特征总共被观测了多少次

  int solve_flag;  // 0 haven't solve yet; 1 solve succ; 2 solve fail;

  lineFeaturePerId(int _feature_id, int _start_frame)
      : feature_id(_feature_id),
        start_frame(_start_frame),
        used_num(0),
        solve_flag(0),
        is_triangulation(false) {
    removed_cnt = 0;
    all_obs_cnt = 1;
  }

  int endFrame();
};

构造的逻辑，理解了之前的对应关系是怎么存储的这里就很好理解了：

 // 遍历同一帧上的线特征
 for (auto &id_line : lines) {
   // 使用起点终点初始化
   lineFeaturePerFrame f_per_fra(id_line.second[0].second);  // 观测
   // 这是与上一帧的匹配关系，也可以认为是全局线特征id
   int feature_id = id_line.first;  
   // cout << "line id: "<< feature_id << "\n";
   // 在feature里找id号为feature_id的特征
   auto it = find_if(linefeature.begin(), linefeature.end(),
                     [feature_id](const lineFeaturePerId &it) {
                       return it.feature_id == feature_id;
                     });
   // 如果之前没存这个特征，说明是新的
   if (it == linefeature.end()) {
     linefeature.push_back(lineFeaturePerId(feature_id, frame_count));
     linefeature.back().linefeature_per_frame.push_back(f_per_fra);
   } else if (it->feature_id == feature_id) {
     it->linefeature_per_frame.push_back(f_per_fra);
     it->all_obs_cnt++;
   }
 }

3.线段三角化

3.1.普吕克线坐标

在图 $2\mathrm{a}$ 中, 普吕克坐标中的 $3\mathrm{D}$ 空间线 $\mathcal{L}$ 由 $\mathcal{L}={\left({\mathbf{n}}^{?},{\mathrm{d}}^{?}\right)}^{?}\in {\mathbb{R}}^6$ 表示, 其中 $\mathrm{d}\in {\mathbb{R}}^3$ 是线方向向量, $\mathrm{n}\in {\mathbb{R}}^3$ 是由直线和坐标原点确定的平面法向量。Plücker 坐标被过度参数化，因为向量 $\mathrm{n}$ 和 $\mathrm{d}$ 之间存在隐式约束，即 ${\mathrm{n}}^{?}\mathrm{d}=0$ 。因此, Plücker坐标不能直接用于无约束优化。然而, 使用由法线向量和方向向量表示的 3D 线, 可以简单地从两个几何视图执行三角测量, 并且也可以方便地对线几何变换进行建模。

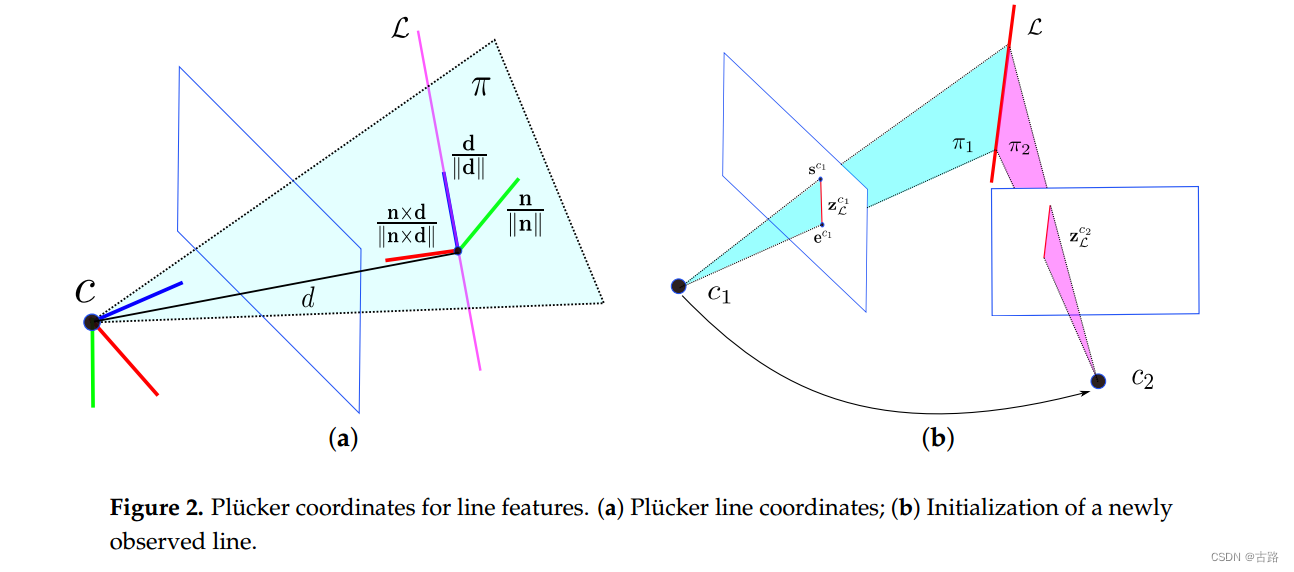
对于线几何变换, 给定从世界坐标系 $\mathrm{w}$ 到相机坐标系 $\mathrm{c}$ 的变换矩阵 ${\mathbf{T}}_{cw}=\left[\begin{array}{cc}{\mathbf{R}}_{cw}& {\mathbf{P}}_{cw}\\ 0& 1\end{array}\right]$, 我们可以将线的 Plücker 坐标变换为 [30]
$${\mathcal{L}}^c=\left[\begin{array}{c}{\mathbf{n}}^c\\ {\mathbf{d}}^c\end{array}\right]=J_{cw}{\mathcal{L}}_w=\left[\begin{array}{cc}{\mathbf{R}}_{cw}& {\left[{\mathbf{p}}_{cw}\right]}_x{\mathbf{R}}_{cw}\\ 0& {\mathbf{R}}_{cw}\end{array}\right]{\mathcal{L}}^w$$

其中 $[?{]}_{\times }$是三维向量的斜对称矩阵， $J_{cw}$ 是用于将线从帧 $w$ 变换到帧 $\mathrm{c}$ 的变换矩阵。

当在两个不同的摄像机视图中观察到新的线地标时，可以轻松计算出普吕克坐标。如图 $2\mathrm{b}$ 所示，3D 线 $\mathcal{L}$ 由摄像机 $c_1$ 和 $c_2$ 捕获为 ${\mathrm{z}}_L^{c_1}$ 和 ${\mathrm{z}}_l^{c_2}$。归一化图像平面中的线段 ${\mathrm{z}}_L^{c_1}$ 可以由两个端点 ${\mathrm{s}}^{c_1}={\left[u_s,v_s,1\right]}^T$ 和 ${\mathrm{e}}^{c_1}={\left[u_e,v_e,1\right]}^{?}$ 表示。三个不共线的点，包括线段的两个端点和坐标原点 $\mathrm{C}={\left[x_0,y_0,z_0\right]}^{?}$, 确定 $3\mathrm{D}$ 空间中的平面 $\pi ={\left[{\pi }_x,{\pi }_y,{\pi }_z,{\pi }_w\right]}^{?}$ :
$${\pi }_x\left(x?x_0\right)+{\pi }_y\left(y?y_0\right)+{\pi }_z\left(z?z_0\right)=0$$
这里
$$\left[\begin{array}{c}{\pi }_x\\ {\pi }_y\\ {\pi }_z\end{array}\right]={\left[{\mathbf{s}}^{c_1}\right]}_{\times }{\mathrm{e}}^{c_1},{\pi }_w={\pi }_x{x}_0+{\pi }_y{y}_0+{\pi }_z{z}_0$$

给定相机坐标系 $c_1$ 中的两个平面 ${\pi }_1$ 和 ${\pi }_2$, 对偶普吕克矩阵 ${\mathrm{L}}^{?}$ 可以通过以下方式计算
$${\mathbf{L}}^{?}=\left[\begin{array}{cc}[\mathbf{d}{]}_{\mathbf{x}}& \mathbf{n}\\ ?{\mathbf{n}}^{?}& 0\end{array}\right]={\pi }_1{\pi }_2^{?}?{\pi }_2{\pi }_1^{?}\in {\mathbb{R}}^{4\times 4}$$

相机坐标系 $c_1$ 中的 Plücker 坐标 $\mathcal{L}$ 很容易从对偶 Plücker 矩阵 $L^{?}$ 中提取。可以看出, $\mathbf{n}$ 和 $\mathrm{d}$ 不需要是单位向量。

主体逻辑在void FeatureManager::triangulateLine(Vector3d Ps[], Vector3d tic[], Matrix3d ric[]) 中：

• 根据线段起点终点相机原点求平面：

/*
 三点确定一个平面 a(x-x0)+b(y-y0)+c(z-z0)=0  --> ax + by + cz + d = 0   d = -(ax0 + by0 + cz0)
 平面通过点（x0,y0,z0）以及垂直于平面的法线（a,b,c）来得到
 (a,b,c)^T = vector(AO) cross vector(BO)
 d = O.dot(cross(AO,BO))
 */
Vector4d pi_from_ppp(Vector3d x1, Vector3d x2, Vector3d x3) {
    Vector4d pi;
    pi << ( x1 - x3 ).cross( x2 - x3 ), - x3.dot( x1.cross( x2 ) ); // d = - x3.dot( (x1-x3).cross( x2-x3 ) ) = - x3.dot( x1.cross( x2 ) )
    return pi;
}

如果两平面夹角小于 15 度，不三角化。两个平面求交线：

// 两平面相交得到直线的plucker 坐标
Vector6d pipi_plk( Vector4d pi1, Vector4d pi2){
    Vector6d plk;
    Matrix4d dp = pi1 * pi2.transpose() - pi2 * pi1.transpose();

    plk << dp(0,3), dp(1,3), dp(2,3), - dp(1,2), dp(0,2), - dp(0,1);
    return plk;
}

 Vector6d plk = pipi_plk(pii, pij);
 Vector3d n = plk.head(3);
 Vector3d v = plk.tail(3);

// ...plk坐标的矩阵形式
 Vector3d pc, nc, vc;
 nc = it_per_id.line_plucker.head(3);
 vc = it_per_id.line_plucker.tail(3);

 Matrix4d Lc;
 Lc << skew_symmetric(nc), vc, -vc.transpose(), 0;

3.2.正交表示

由于 $3\mathrm{D}$ 空间线只有四个自由度, 因此在优化过程中, 正交表示 $(\mathbf{U},\mathbf{W})\in SO(3)\times SO(2)$ 比 Plücker 坐标更合适。此外，正交表示和普吕克坐标可以相互转换，这意味着我们可以在 SLAM 系统中出于不同的目的同时采用它们。在本节中，我们将介绍正交表示的详细信息。如图 $2\mathrm{a}$ 所示，在 3D 线上定义了坐标系。归一化法向量和归一化方向向量是坐标系的两个轴。第三轴是通过与其他两个轴向量相交来确定的。我们可以将线坐标和相机框架之间的旋转矩阵定义为 $\mathbf{U}$ :
$$\mathbf{U}=\mathbf{R}(\psi )=\left[\begin{array}{lll}\frac{\mathrm{n}}{||\mathrm{n}||}& \frac{\mathrm{d}}{||\mathrm{d}||}& \frac{\mathrm{n}\times \mathrm{d}}{||\mathrm{n}\times \mathrm{d}|\mid }\end{array}\right]$$

其中 $\psi ={\left[{\psi }_1,{\psi }_2,{\psi }_3\right]}^{?}$ 由相机框架绕 $x、y$ 和 $\mathrm{z}$ 轴的旋转角度组成。普吕克坐标与 $\mathrm{U}$ 之间的关系为:
$$\left[\begin{array}{ll}\mathbf{n}& \mathbf{d}\end{array}\right]=\left[\begin{array}{lll}\frac{\mathrm{n}}{\Vert \mathrm{n}\Vert }& \frac{\mathrm{d}}{\Vert \mathrm{d}\Vert }& \frac{\mathrm{n}\times \mathrm{d}}{\Vert \mathrm{n}\times \mathrm{d}\Vert }\end{array}\right]\left[\begin{array}{cc}\Vert \mathbf{n}\Vert & 0\\ 0& \Vert \mathrm{d}\Vert \\ 0& 0\end{array}\right]$$

由于式(16)中 $(\Vert \mathbf{n}\Vert ,\Vert \mathrm{d}\Vert )$ 的组合只有一个DoF，我们可以用三角函数来表示：
$$\mathbf{W}=\left[\begin{array}{cc}\cos (?)& ?\sin (?)\\ \sin (?)& \cos (?)\end{array}\right]=\frac{1}{\sqrt{\left(\Vert \mathbf{n}{\Vert }^2+\Vert \mathbf{d}{\Vert }^2\right)}}\left[\begin{array}{cc}\Vert \mathbf{n}\Vert & ?\Vert \mathbf{d}\Vert \\ \Vert \mathbf{d}\Vert & \Vert \mathbf{n}\Vert \end{array}\right]$$

其中 $?$ 是旋转角度。回想一下, 从坐标原点到 $3\mathrm{D}$ 线的距离是 $d=\frac{\Vert \mathrm{n}\Vert }{\Vert \mathrm{d}\Vert }$, 因此 $\mathbf{W}$ 包含有关距离 $\mathrm{d}$ 的信息。根据 $\mathrm{U}$ 和 $\mathbf{W}$ 的定义, 这四个 DoF 包括来自旋转矩阵 (将线坐标变换到相机坐标系) 的 3 个 DoF, 以及来自距离 $\mathrm{d}$ 的 1 个 $\mathrm{DoF}$ 。我们在优化过程中使用 $O=[\psi ,?{]}^{?}$ 作为 3D 空间线的最小表示。

使用正交表示优化 3D 线 $\mathcal{L}$ 后，可以通过以下方式计算该线相应的普吕克坐标:
$${\mathcal{L}}^{\prime }={\left[w_1{\mathbf{u}}_1^T,w_2{\mathbf{u}}_2^T\right]}^T=\frac{1}{\sqrt{\left(\mid \mathbf{n}\Vert {}^2+\Vert \mathbf{d}{\Vert }^2\right)}}\mathcal{L}$$

其中 ${\mathbf{u}}_i$ 是矩阵 $\mathbf{U}$ 的第 $i$ 列、 $w_1=\cos (?)$ 和 $w_2=\sin (?)$ 。 ${\mathcal{L}}^{\prime }$ 和 $\mathcal{L}$ 之间存在比例因子，但它们代表相同的3D空间线。

• plk转正交表示

  Vector4d plk_to_orth(Vector6d plk) {
    Vector4d orth;
    Vector3d n = plk.head(3);
    Vector3d v = plk.tail(3);
  
    Vector3d u1 = n / n.norm();
    Vector3d u2 = v / v.norm();
    Vector3d u3 = u1.cross(u2);
  
    // todo:: use SO3
    orth[0] = atan2(u2(2), u3(2));
    orth[1] = asin(-u1(2));
    orth[2] = atan2(u1(1), u1(0));
  
    Vector2d w(n.norm(), v.norm());
    w = w / w.norm();
    orth[3] = asin(w(1));
  
    return orth;
  }
  

• 正交表示转plk

  Vector6d orth_to_plk(Vector4d orth) {
    Vector6d plk;
  
    Vector3d theta = orth.head(3);
    double phi = orth[3];
  
    double s1 = sin(theta[0]);
    double c1 = cos(theta[0]);
    double s2 = sin(theta[1]);
    double c2 = cos(theta[1]);
    double s3 = sin(theta[2]);
    double c3 = cos(theta[2]);
  
    Matrix3d R;
    R << c2 * c3, s1 * s2 * c3 - c1 * s3, c1 * s2 * c3 + s1 * s3, c2 * s3,
        s1 * s2 * s3 + c1 * c3, c1 * s2 * s3 - s1 * c3, -s2, s1 * c2, c1 * c2;
  
    double w1 = cos(phi);
    double w2 = sin(phi);
    double d = w1 / w2;  // 原点到直线的距离
  
    Vector3d u1 = R.col(0);
    Vector3d u2 = R.col(1);
  
    Vector3d n = w1 * u1;
    Vector3d v = w2 * u2;
  
    plk.head(3) = n;
    plk.tail(3) = v;
  
    // Vector3d Q = -R.col(2) * d;
    // plk.head(3) = Q.cross(v);
    // plk.tail(3) = v;
  
    return plk;
  }
  

优化的时候使用正交表示。这部分操作位于line_geometry.h/cpp

4.线段对位姿的导数

• todo