Java LeetCode篇-深入了解二叉树的经典解法（多种方式实现：构造二叉树）

题目：

????????给定两个整数数组?preorder?和?inorder?，其中?preorder?是二叉树的先序遍历，?inorder?是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
OJ链接：

105.?从前序与中序遍历序列构造二叉树

? ? ? ? 1.1 实现从前序与中序遍历序列来构造二叉树思路? ?

????????具体思路为：前序遍历的流程先是访问根节点，到左子树，再到右子树的顺序；中序遍历的流程先是左子树，到访问根节点，再到右子树。因此，在前序的序列中的第一个元素就是该树的根节点的值，然后再通过中序的序列中遍历找根节点。接着就可以将其中序的序列进行拆分，在中序序列中根节点的值的左边部分的序列为左子树，在中序序列中根节点的值的右边部分序列为右子树。又接着将前序序列进行拆分，从索引为 1 开始，长度为：与中序序列中左子树的序列数量是一致的，将这一部分称为左子树；从索引（1+长度）开始到该序列的结束，将这一部分称为右子树。接下来就是子问题了，通过递归，找到当前节点的左右子树。

? ? ? ?具体例子：前序序列 pre = {3,9,20,15,7}，中序序列 in = {9,3,15,20,7} 。先找到该树的节点值 int rootValue = pre[0]， TreeNode root = new TreeNode(rootValue)，创建该树的根节点。接着对中序序列遍历来找到根节点的值，i == 1 ，在中序序列中找左右子树：在索引在该区间 [0,1）是节点的左子树，而在索引为?[2,5）区间是节点的右子树。在前序序列中找左右子树：在索引为 [1,2）是该节点的左子树，而在索引为 [2,5）区间是节点的右子树。

? ? ? ? 子问题：那么现在得到了左子树的前序序列 pre = { 9 } ，左子树的中序序列 in = { 9 }，接下来的流程跟以上的流程是一样的，先找到该子树的根节点值 9 ，然后创建一个值为 9 的根节点。接着，遍历中序序列来找到根节点的值，该根节点的左部分就是左子树，该节点的右部分就是右子树。那么这里的左右子树都为空，因此节点为 9 的根节点没有左右子树了。

? ? ? ? 往上回溯：来到根节点值为 3 的节点。现在得到了右子树的前序序列 pre = {20,15,7} ，右子树的中序序列 in = {15,20,7} ，接下来的过程是一摸一样的，先找到该子树的根节点值为 20 ，创建值为 20 的根节点。然后在中序序列中进行遍历找到根节点的左右子树：左子树序列为 {15}，右子树序列为 {7}，接着在前序序列中找左右子树：左子树序列为 {15}，右子树序列为 {7} 。又得到了左右前中序列，按同样的道理继续下去即可，通过上面的结论，当左子树前序 {15} 与左子树中序 {15} 一样时，那么在当前的节点值为 15 的根节点没有左右子树了。同理，当右子树前序 {7} 与右子树中序 {7} 一样时，那么在当前的节点值为 7 的根节点没有左右子树了。

? ? ? ? 最后回溯，根节点值为 20 的左子树的根节点为 15，右子树的根节点为 7 ，链接起来，一直回溯到结束返回的最后的节点就是该树的根节点（值为 1 的根节点）。

? ? ? ? 需要注意的是：注意左闭右开。因为是同一颗树，在前序中的左右子树的长度跟中序中的左右子树的长度是一样的。

? ? ? ? 1.2 代码实现从前序与中序遍历序列来构造二叉树

    //根据前序与中序来构造二叉树
    public TreeNode prevAndInOrderConstructTree(int[] prevOrder, int[] inOrder) {
        if (prevOrder.length == 0) {
            return null;
        }
        int rootValue = prevOrder[0];
        TreeNode root = new TreeNode(rootValue);
        for (int i = 0; i < inOrder.length; i++) {
            if (inOrder[i] == rootValue) {
                int[] inLeft = Arrays.copyOfRange(inOrder,0,i);
                int[] inRight = Arrays.copyOfRange(inOrder,i+1,inOrder.length);

                int[] prevLeft = Arrays.copyOfRange(prevOrder,1,i + 1);
                int[] prevRight = Arrays.copyOfRange(prevOrder,i+1,inOrder.length);

                root.left = prevAndInOrderConstructTree(prevLeft,inLeft);
                root.right = prevAndInOrderConstructTree(prevRight,inRight);
            }
        }
        return root;
    }

? ? ? ? 只要某一个序列无论是前序或者是中序序列的长度为 0 ，都代表创建二叉树过程结束了。

? ? ? ? 2.0 从中序与后序遍历序列构造二叉树

题目：

????????给定两个整数数组?inorder?和?postorder?，其中?inorder?是二叉树的中序遍历，?postorder?是同一棵树的后序遍历，请你构造并返回这颗?二叉树?。

示例 1:
输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]
OJ链接：

106.?从中序与后序遍历序列构造二叉树

? ? ? ? 2.1 实现从中序与后序遍历序列后遭二叉树思路

? ? ? ? 具体思路为：中序的序列先访问左子树，再访问根节点，最后到右子树。后序的序列先访问左子树，再访问右子树，最后才到根节点。因此，可以从后序序列中的最后一个元素得到根节点的值，然后利用该值来创建根节点。接着，在中序序列中遍历查找根节点的值，在中序序列中根节点值左边的序列为左子树序列，在中序序列中根节点的右边为右子树的序列。再接着再后序中获取左子树的序列：从索引为 0 开始长度是中序序列得到的左子树的长度；从后序序列中获取右子树序列：除了左子树的序列和根节点值元素，其余就是右子树的序列了。接下来就是子问题了，递归下去，返回当前的根节点。

? ? ? ? 具体例子：中序序列 in = {9,3,15,20,7}，后序序列 post = {9,15,7,20,3}，通过后序得到该树的根节点的值 3，由这个值来创建值为 3 的根节点。接着通过遍历中序序列，找到值为 3 来定位左右子树，左子树的序列为：{9} ，右子树的序列为：{15,20,7} 。再从中序序列中定位左右子树，左子树为：{9}，右子树为：{15，7，20} 。现在得到了左右中后序列，中序左子树：{9} ，后序左子树：{9}，通过后序得到根节点，再从中序定位该子树的根节点，这里根节点值为 9 的根节点的左右子树均为 null 。接着回溯，返回的该子树的根节点。

? ? ? ? 再到右子树中序 {15,20,7} ，右子树后序 {15,7,20}，通过后序序列的最后一个值来创建该子树的根节点，在中序中遍历找到该根节点的值，定位该节点的左右子树。中序的左子树序列 {15}，右子树序列 {7}；后序的左子树序列 {15}，后序的右子树序列 {7} 。

? ? ? ? 再接着递归，得到左子树中序 {15} ，左子树后序 {15}。通过后序的最后一个元素就是根节点的值来创建该子树的根节点，然后在中序中定位该根节点的左右子树，这里的左右子树都为 null ，返回根节点即可。得到右子树中序 {7}，右子树后序 {7}，通过后序的最后一个元素为根节点的值来创建该子树的根节点，然后在中序中定位该根节点的左右子树，恰好，这里的左右子树都为 null ，返回根节点即可。

? ? ? ? 最后回溯过程，根节点值为 1 的节点的左子树的根节点为 9 的节点，右子树的根节点为 20 的节点。

? ? ? ? 2.2 代码实现从中序与后序遍历序列来构造二叉树

    //根据中序与后序来构造二叉树
    public TreeNode inAndPostConstructTree(int[] inOrder, int[] postOrder) {

        if (inOrder.length == 0) {
            return null;
        }
        int rootValue = postOrder[postOrder.length-1];
        TreeNode root = new TreeNode(rootValue);
        for (int j = 0; j < inOrder.length; j++) {
            if (rootValue == inOrder[j]) {
                int[] inLeft = Arrays.copyOfRange(inOrder,0,j);
                int[] inRight = Arrays.copyOfRange(inOrder,j+1,inOrder.length);

                int[] postLeft = Arrays.copyOfRange(postOrder,0,j);
                int[] postRight = Arrays.copyOfRange(postOrder,j,postOrder.length-1);

                root.left = inAndPostConstructTree(inLeft,postLeft);
                root.right = inAndPostConstructTree(inRight,postRight);
            }
        }
        return root;

    }

? ? ? ? 需要注意的定位左右子树的序列长度，中序与后序的左右子树都是一一对应的。也因此，当无论任意一个序列结束，都代表着构造二叉树过程结束。

? ? ? ? 3.0 根据后缀表达式创建二叉树

????????后缀表达式也叫逆波兰表达式，是一种不需要括号的表达式表示方法。在后缀表达式中，运算符总是在操作数的后面，因此可以通过从左到右扫描表达式来创建二叉树。

? ? ? ? 3.1 实现后缀表达式创建二叉树思路

? ? ? ? 具体思路为：若遇到数字将其压入栈中；若遇到操作符时，将栈中的右左元素弹出栈，操作符节点进行链接弹出来的左右子树，需要注意的是，第一个弹出来的是右操作数，第二个才是左操作数。链接完之后，将其压入栈中即可。循环结束条件为：将后缀表达式遍历完就结束。最后返回栈中的栈顶元素，就是该树的根节点。

? ? ? ? 3.2 代码实现后缀表达式创建二叉树

    //根据后缀表达式创建二叉树
    public TreeNode suffixCreateTree(String[] s) {

        LinkedList<TreeNode> stack = new LinkedList<>();
        for (int i = 0; i < s.length; i++) {
            String ch = s[i];
            switch (ch) {
                case "+","-","*","/" -> {
                    TreeNode right = stack.pop();
                    TreeNode left = stack.pop();
                    TreeNode t = new TreeNode(ch);
                    t.right = right;
                    t.left = left;
                    stack.push(t);
                }
                default -> {
                    stack.push(new TreeNode(ch));
                }
            }

        }
        return stack.peek();
    }

? ? ? ? ?4.0 相同的树

题目：

????????给你两棵二叉树的根节点?p?和?q?，编写一个函数来检验这两棵树是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

示例 1：
输入：p = [1,2,3], q = [1,2,3]
输出：true
OJ链接：

100.?相同的树

? ? ? ? 4.1 实现判断两颗树是否相同思路

? ? ? ? 具体思路为：使用递归实现，第一种情况：若一个子树为 null ，另一个子树不为 null ，返回 false ；第二种情况：若两个子树都为 null ，则返回 true 。第三种情况：若两个子树的根节点的值不相同时，返回 false 。子过程，判断完左子树，还需判断右子树。

? ? ? ? 4.2 代码实现相同树

class Solution {
    public boolean isSameTree(TreeNode p, TreeNode q) {
        if( p != null && q == null || p ==null && q != null) {
            return false;
        }
        if(p == null && q == null ){
            return true;
        }
        if(p.val != q.val) {
            return false;
        }
        return isSameTree(p.left, q.left) && isSameTree(p.right,q.right);
    }
}

? ? ? ? 5.0 另一颗树的子树

题目：

????????给你两棵二叉树?root?和?subRoot?。检验?root?中是否包含和?subRoot?具有相同结构和节点值的子树。如果存在，返回?true?；否则，返回?false?。

二叉树?tree?的一棵子树包括?tree?的某个节点和这个节点的所有后代节点。tree?也可以看做它自身的一棵子树。

示例 1：
输入：root = [3,4,5,1,2], subRoot = [4,1,2]
输出：true
OJ链接:

572.?另一棵树的子树

? ? ? ? ?5.1 实现判断是否为另一颗树的子树

? ? ? ? 具体思路为：最根本的问题就是判断是否为相同的树，判断该树的子树与另一颗子树是否相同，不断递归下去，只要相同就返回 true 。直到最后递归结束都没有匹配，则返回 false 。

? ? ? ? 5.2 代码实现判断是否为另一颗树的子树

class Solution {
    public boolean isSubtree(TreeNode root, TreeNode subRoot) {
        if(root == null) {
            return false;
        }
        if(isSameTree(root,subRoot)) {
            return true;
        }
        if(isSubtree(root.left,subRoot)) {
            return true;
        }
        if(isSubtree(root.right,subRoot)) {
            return true;
        }
        return false;

    }
        public boolean isSameTree(TreeNode p, TreeNode q) {
        if( p != null && q == null || p ==null && q != null) {
            return false;
        }
        if(p == null && q == null ){
            return true;
        }
        if(p.val != q.val) {
            return false;
        }
        return isSameTree(p.left, q.left) && isSameTree(p.right,q.right);
    }
}

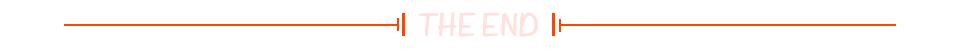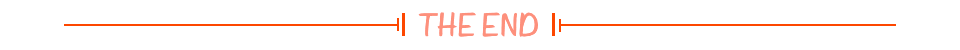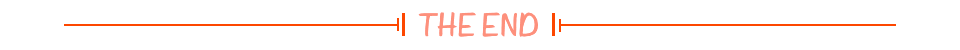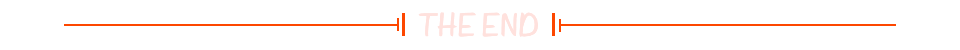
文章来源:https://blog.csdn.net/Tingfeng__/article/details/134885049
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：veading@qq.com进行投诉反馈，一经查实，立即删除！