Python算法例30 统计前面比自己小的数
2023-12-28 11:28:43
1. 问题描述
给定一个整数数组(数组大小为n,元素的取值范围为0~10000),对于数组中的每个元素,计算其前面元素中比它小的元素数量。
2. 问题示例
对于数组[1,2,7,8,5],返回[0,1,2,3,2]。
3. 代码实现
使用暴力法实现,对于数组中的每个元素,遍历它前面的元素,统计比它小的元素的数量。
def count_smaller_elements(nums):
result = []
for i in range(len(nums)):
count = 0
for j in range(i):
if nums[j] < nums[i]:
count += 1
result.append(count)
return result
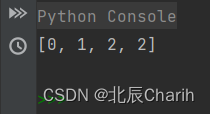
nums = [1, 2, 7, 5]
result = count_smaller_elements(nums)
print(result) 这个算法的时间复杂度是O(n^2),其中n是数组的大小。
使用树状数组(Binary Indexed Tree)实现
树状数组(Binary Indexed Tree)是一种用于高效查询和修改序列前缀和的数据结构。它可以在 O(logn) 的时间内进行单点修改和查询操作,同时支持快速计算任意前缀和。
树状数组的核心思想是利用二进制的特性,将序列分解为若干个区间,并预处理每个区间的和。这些区间的长度为 2 的幂次方,且每个区间的和等于其最后一个元素及之前所有元素的和。通过对这些区间的和进行运算,可以得到序列中任意前缀和的值。
在使用树状数组时,需要先创建一个
BinaryIndexedTree对象,然后通过调用update方法来修改树状数组的值。修改完成后,可以使用query方法来查询任意前缀和的值。class BinaryIndexedTree: def __init__(self, n): self.n = n self.tree = [0] * (n + 1) def update(self, index, value): index += 1 while index <= self.n: self.tree[index] += value index += index & (-index) def query(self, index): index += 1 result = 0 while index > 0: result += self.tree[index] index -= index & (-index) return result上述代码中,BinaryIndexedTree 类表示树状数组,其中 n 表示数组的长度,tree 保存了数组的值。update 方法用于更新树状数组的值,query 方法用于查询指定下标的前缀和。
def update(bit, index, value):
index += 1
while index < len(bit):
bit[index] += value
index += index & (-index)
def query(bit, index):
index += 1
result = 0
while index > 0:
result += bit[index]
index -= index & (-index)
return result
def count_smaller_elements(nums):
n = len(nums)
bit = [0] * (max(nums) + 1)
result = []
for i in range(n):
result.append(query(bit, nums[i] - 1))
update(bit, nums[i], 1)
return result
# 示例测试
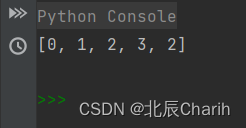
nums = [1, 2, 7, 8, 5]
result = count_smaller_elements(nums)
print(result) # 输出 [0, 1, 2, 3, 2]
这段代码使用了树状数组来优化计算过程,时间复杂度为 O(nlogn)。在遍历数组时,对于当前元素,通过树状数组快速查询比它小的元素数量,并更新树状数组以记录当前元素的出现。
因此,这种实现方式在处理大规模数据时具有较高的效率。
文章来源:https://blog.csdn.net/m0_62110645/article/details/135258045
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!