运筹学经典问题(二):最短路问题
问题描述
给定一个图(有向图或无向图)
G
=
(
V
,
E
)
G = (V, E)
G=(V,E),
V
V
V是图中点的集合,
E
E
E是图中边的集合,图中每条边
(
i
,
j
)
∈
E
(i, j) \in E
(i,j)∈E都对应一个权重
c
i
j
c_{ij}
cij?(距离或者运输成本等),给定一个起点
u
u
u和一个终点
z
z
z,最段路问题就是寻找一条从
s
s
s出发,到达
z
z
z的距离最短或者成本最低的路径。
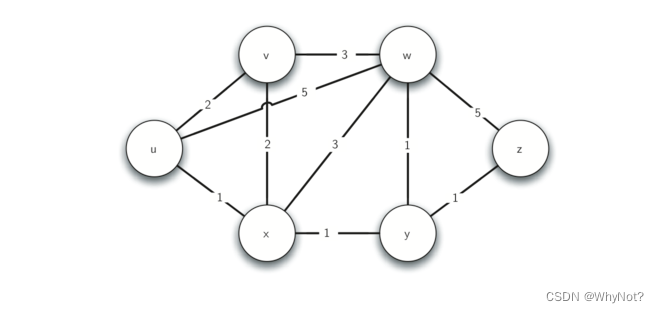
数学建模
定义:
I
I
I:点的集合;
o
u
t
(
i
)
out(i)
out(i):离开点
i
i
i边的集合;
i
n
(
i
)
in(i)
in(i):进入点
i
i
i边的集合;
x
e
x_e
xe?:是否选择
e
e
e这条边,0-1变量;
m
i
n
∑
e
∈
E
x
e
c
e
s
.
t
.
∑
e
∈
o
u
t
(
i
)
x
e
?
∑
e
∈
i
n
(
i
)
x
e
=
{
1
,
i
=
u
?
1
,
i
=
z
0
,
e
l
s
e
min \sum_{e \in E}x_ec_e \\ s.t. \sum_{e \in out(i)}x_e - \sum_{e \in in(i)}x_e= \begin{cases} 1, i=u \\ -1, i=z \\ 0, else \end{cases}
mine∈E∑?xe?ce?s.t.e∈out(i)∑?xe??e∈in(i)∑?xe?=?
?
??1,i=u?1,i=z0,else?
上述模型优化目标为最小化路径距离,约束为进出平衡(分了3种点的类型去写约束:始发点只出不进、目的点只进不出、其他点进等于出)。
整数最优解特性
即使把变量 x e x_{e} xe?松弛成 0 ≤ x e ≤ 1 0 \leq x_e \leq1 0≤xe?≤1,原问题变成线性规划,该问题仍然存在整数最优解。
模型求解
调用求解器求解即可。
- 后面补充代码。
参考资料
- 最短路径问题.
- 运筹优化常用算法、模型及案例实战:Python+Java 实现. 刘兴禄,熊望祺,臧永森,段宏达,曾文佳,陈伟坚.
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!