traj_dist 笔记 源代码解析（python部分）

1distance.py

1.1 METRIC_DIC

不同实现方法对应的函数路径

1.2?sspd

功能：

• 计算轨迹 traj_1 和 traj_2 之间的对称化段路径距离。

参数：

• traj_1：一个二维 numpy 数组，代表第一个轨迹。
• traj_2：一个二维 numpy 数组，代表第二个轨迹。
• type_d：字符串，指定距离的类型（"euclidean" 或 "geographical"）。
  • "euclidean" 表示使用欧几里得距离，适用于任何维度的轨迹。
  • "geographical" 表示使用地理距离，假设轨迹是二维的，第一维是经度，第二维是纬度。
• implementation：字符串，指定实现方式（"python"、"cython" 或 "auto"）。
  • 如果轨迹是二维的，默认使用 Cython 实现；否则使用 Python 实现，除非明确指定为 "python"。

返回值：

• 返回一个浮点数，表示两个轨迹之间的对称化段路径距离。

1.3??sowd_grid

两个轨迹之间的对称化单向距离（Symmetrized One-Way Distance）

大体逻辑和1.2 相同，这边多了两个内容

• converted：布尔值，如果为 True，则表示轨迹已经转换为网格表示形式
• precision：Geohash 精度，用于地理坐标的转换。
• 'sowd_grid' 计算网格表示中轨迹之间的距离。
  • 如果坐标是地理的，可以根据 geohash 编码进行转换。如果是这样，需要 geohash 的“精度”。
  • 否则，轨迹被认为是以单元格表示编码的。

1.4?frechet

1.5?discret_frechet

1.6?hausdorff

1.7?dtw

逻辑和sspd一样（1.2节），略过

1.8?lcss

1.9?edr

逻辑和sspd一样（1.2节），只是多了一个eps（阈值），略过

1.10?erp

逻辑和sspd一样（1.2节），只是多了一个g（比较基准点），略过

1.11?pdist

用于计算轨迹列表（traj_list）中每对轨迹之间的成对距离

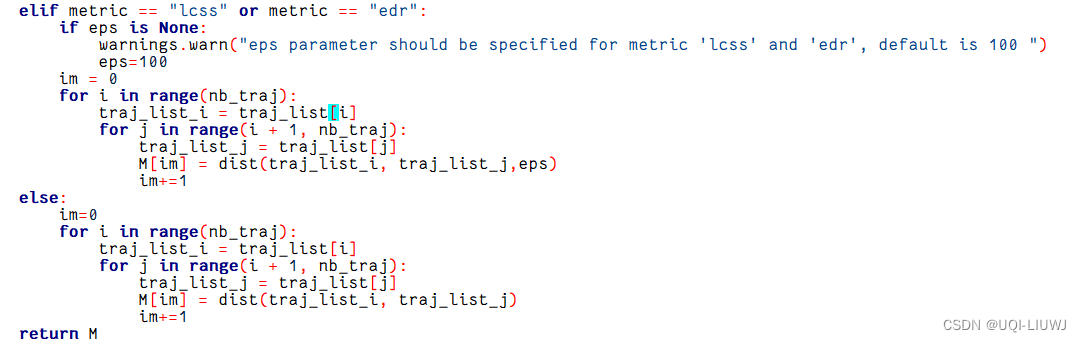
1.12 cdist?

用于计算两个轨迹列表（traj_list_1 和 traj_list_2）中每对轨迹之间的距离

实现逻辑和pdist几乎一模一样，唯一的区别就是一个返回的是一维向量，一个是二维数组

2 pdist/basic_euclidean.py 欧氏距离轨迹相关基本操作

2.1?eucl_dist(x,y)?两个坐标点的差的二范数

简单的两个坐标点的差的二范数

2.2 point_to_seg?点到线段的距离

2.3?point_to_trajectory? 一个点与一条轨迹的最短距离

2.4??circle_line_intersection 圆和线段的交点

?2.4.1 二次方程的推导

2.4.2? 推导坐标

3 basic_geographical.py? 地理空间相关的操作

3.1?great_circle_distance 两个经纬度的大圆距离

3.2?initial_bearing 一个点到另一个点的初始方位角?

3.3 cross_track_distance? 点到大圆路径的距离

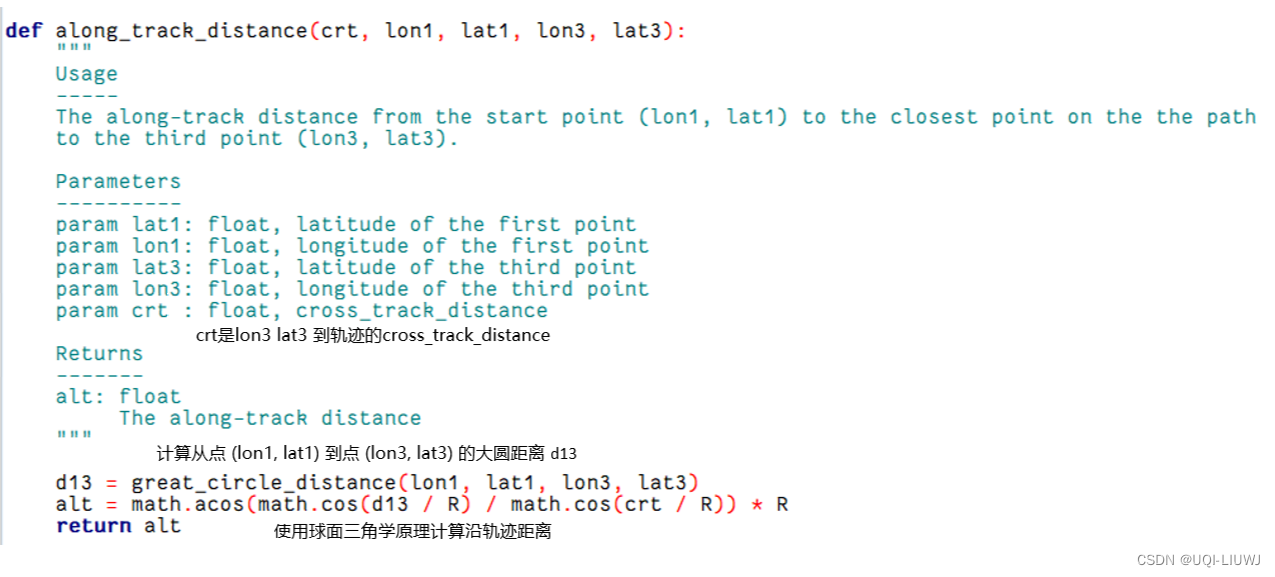
3.4?along_track_distance? 从轨迹上点到不在轨迹上点的沿轨迹距离

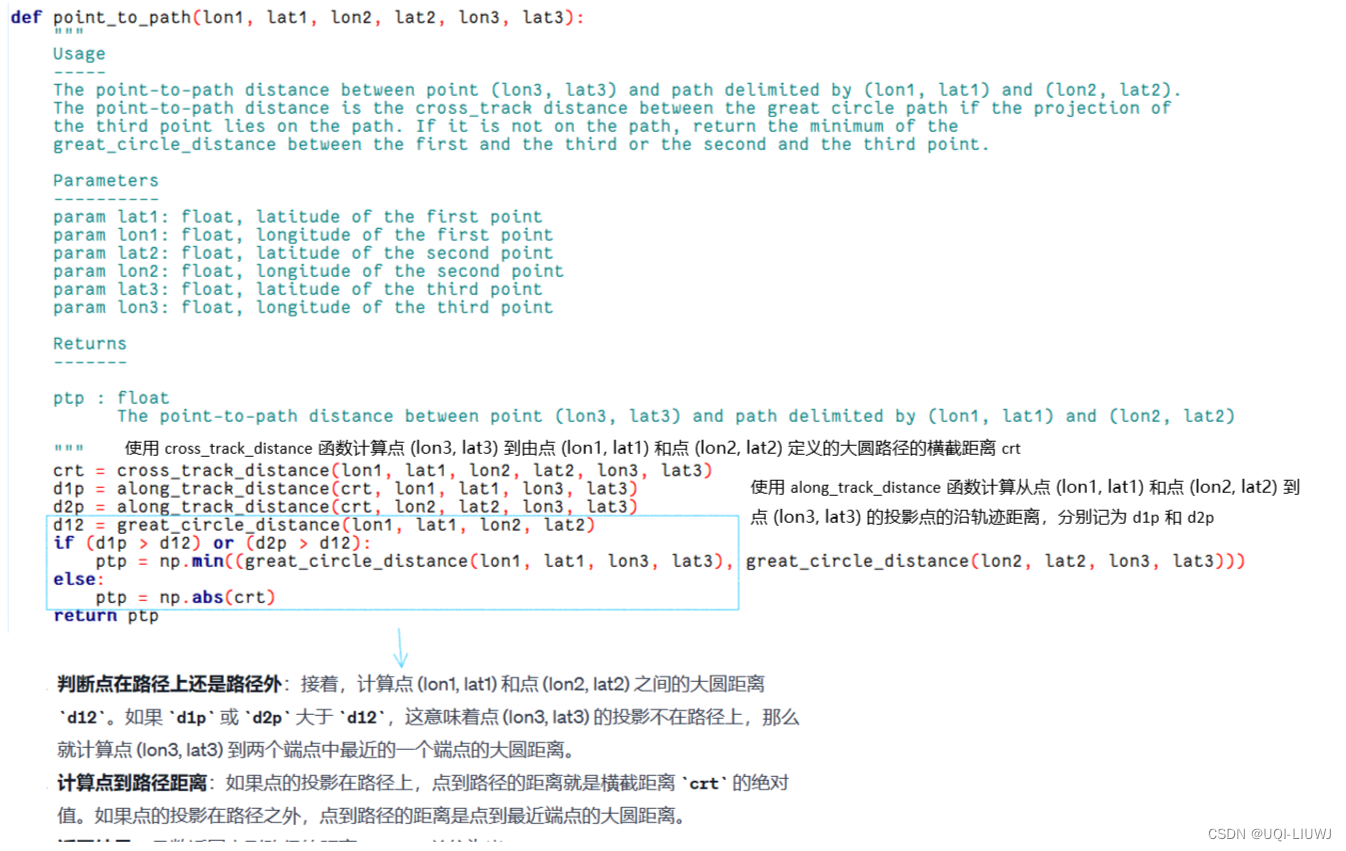
3.5 point_to_path??一个点? 到一条由两点 和? 定义的路径的点到路径距离

4 pdist/sspd.py 一条轨迹上的点到零一条轨迹的距离

4.1?e_spd?轨迹 t1 上的所有点到轨迹 t2 的?? 点到轨迹的距离?

4.2 e_sspd?两个轨迹之间相互的 spd-距离的平均值

4.3? ?g_spd 轨迹 t1 上所有点到轨迹 t2 的? 平均点到路径距离（？）

这里代码的注释是轨迹 t1 上所有点到轨迹 t2 的? 平均点到路径距离，我觉得应该是t2到t1？

4.4?g_sspd?两个轨迹之间相互的 spd-距离的和

注：和欧几里得的版本不同，几何空间版本是求和，而不是取平均

5 pdist/lcss.py 最长公共子序列

5.1 e_lcss

大体上和文巾解题1143. 最长公共子序列-CSDN博客是一样的，仅有一点点区别

5.2 g_lcss

基本上都是一样的，把计算欧几里得距离换成了计算大圆距离?

6?pdist/hausdorff.py?豪斯多夫距离

6.1?e_directed_hausdorff t1到t2的豪斯多夫距离

?6.2?e_hausdorff 双向豪斯多夫

t1到t2和t2到t1的单向豪斯多夫距离中较大的那个

6.3?g_directed_hausdorff

6.4?g_hausdorff

和欧氏距离的唯一区别是，point_to_trajectory改成了point_to_path

7? pdist/erp.py

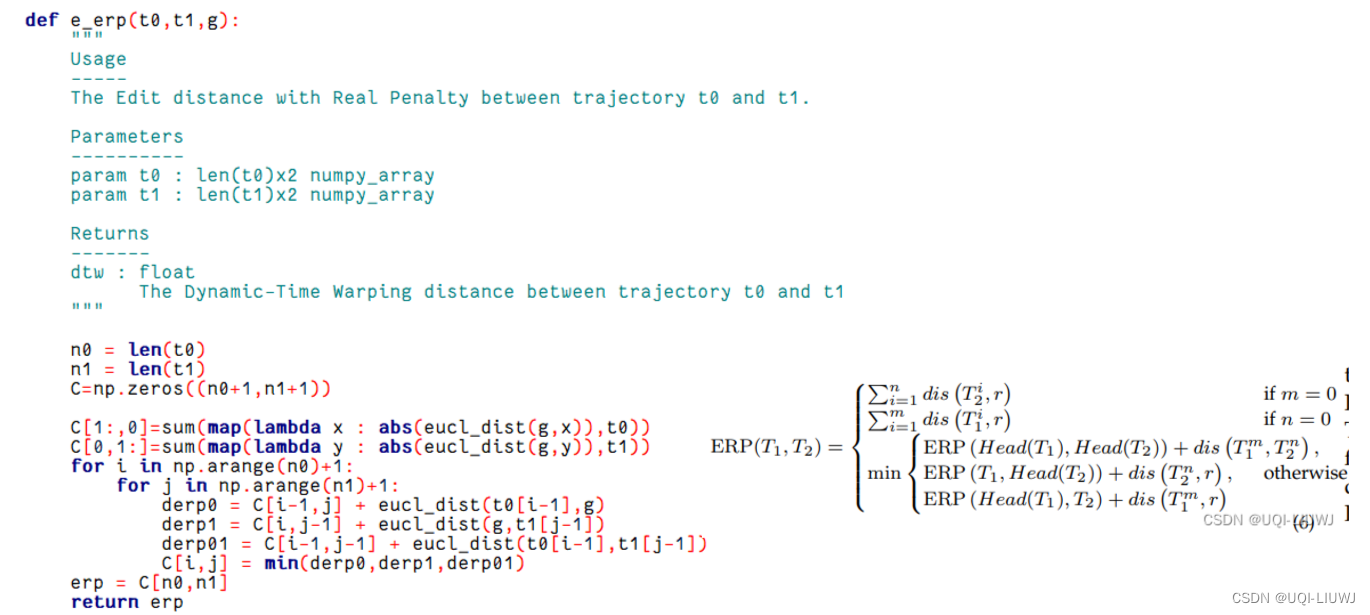
地理坐标类的就是将欧氏距离改成大圆距离

8 pdist/edr.py

8 pdist/dtw.py

?

7数学笔记/scipy 笔记：豪斯多夫距离（Hausdorff ）_python 豪斯多夫距离-CSDN博客